Small angle neutron scattering, SANS
Co-authors: Jakob Kirkensgaard and Lise Arleth, University of Copenhagen, Niels Bohr Institute
Elastic neutron scattering, or neutron diffraction, was first used to reveal the crystal structure of materials, as will be presented in the page on Diffraction from crystals. First, however, we consider the conceptually simpler - but historically later developed - field of (elastic) small angle neutron scattering (SANS), which provides information on the size and shape of particles on length scales from ~1 nm to ~1000 nm.
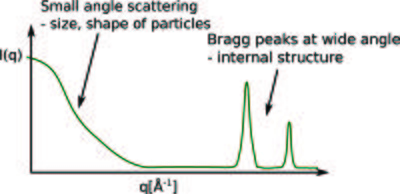
As we shall see later, scattering at small angles - or small values of the scattering vector, \(q\) - is a signature of larger objects, while scattering at larger \(q\)-values probes the atomic distance. This is illustrated in Figure xx--CrossReference--fig:Ursula1--xx.
Applications of SANS in nanoscience
We here start with a few introductory examples to the types of science, where small-angle neutron scattering is useful.
Polymers
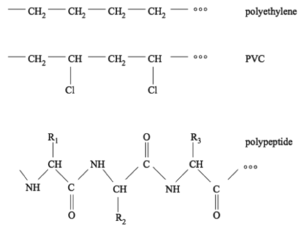
A very important class of molecules are polymers. As the name suggests, a polymer is built by assembling many chemical building blocks: monomers. Typically, this would be into single long chains, although a number of branched architectures also exist. The chains are formed by chemical bonds between the monomers. Conceptually you can think of polymers as beads on a string. Almost everything surrounding us in our daily life is made of polymers, for example plastics, rubber (typically built from one or two types of monomers), and biological molecules like DNA and proteins/peptides (built from several to many types of monomers). Figure xx--CrossReference--fig:JJKK1--xx shows examples of two simple plastic types (polyethylene and PVC), as well as an example of a peptide/protein-like structure.
Some of the most important characteristics of polymers are structural signatures like their size, shape and flexibility, often under different circumstances like varying temperature. For example, polyethylene is very flexible, while DNA is very stiff. The size of the polymer relates to its length, also called the degree of polymerization, i.e. how many monomers, \(N\), it is built from. A typical size measure in polymer science is the radius of gyration which is generally defined as the root mean square distance \(R_g\) of an object's parts from its center of mass
\begin{equation}\label{eq_rg} R_g^2 = \frac{1}{N}\sum_{n=1}^N \langle (\bar{R}_n-\bar{R}_G)^2 \rangle, \end{equation}
where \(R_n\) and \(R_G\) are the position vectors for the object parts and its centre of mass respectively. For a so-called ideal chain polymer this is given by
\begin{equation} R_g^2 = \frac{1}{6}Nb^2, \end{equation}
where \(b\) is the polymer segment (bond) length. For non-ideal (real) chains the size scaling does not obey \(R_g \propto N^{1/2}\) but depends on external parameters, for example whether it is surrounded by a solvent. The structural properties of polymers are typically investigated by scattering methods.
Lipids and surfactants
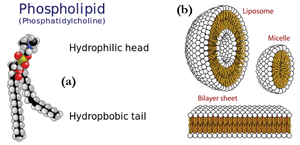
Other polymer-related classes of materials comprise lipids and surfactants, which play a significant role in biology and nano-science. These consist of amphiphilic molecules, i.e. they are made from components that are for example hydrophobic and hydrophilic (water hating and loving, respectively). Examples of such molecules are shown in Figure xx--CrossReference--fig:JJKK2--xx(a).
Lipids are extremely important in biology as they are the building blocks of cells and membranes. Amphiphilic molecules self-assemble in solution to form aggregated structures. The shape and size of these structures can be explored in detail using scattering methods. Figure xx--CrossReference--fig:JJKK2--xx(b) show examples of some of the simplest lipid aggregates, namely micelles and vesicles.
- ↑ Kim Sneppen and Giovanni Zocchi. Physics in Molecular Biology. Cambridge University Press, 2005.
The neutron scattering cross section from nano-sized particles
We will now describe in mathematical terms the scattering from a system of nano-sized particles.
The cross section for neutron diffraction
Our starting point is the expression for the coherent elastic scattering cross section for a system of nuclei from the Basics of neutron scattering page,
\begin{equation}\label{dummy1945322425} \dfrac{d\sigma}{d\Omega}\biggr|_{\rm nucl.\, coh.\, el.} = \biggr|\displaystyle\sum_{j'} b_{j'} \exp(i {\mathbf q} \cdot {\mathbf r}_{j'})\biggr|^2 . \end{equation}
We have here considered the nuclei as being fixed in position. This is a very good approximation for small-angle scattering. For more details on this static approximation and on the necessary corrections to the equation, see the page on Scattering from lattice vibrations on the effect of nuclear vibrations.
The structure factor
For a sample of \(N\) nano-sized particles, we can divide the sum of the scattering nuclei into a sum over particles and a sum over the nuclei within each particle. We now write the nuclear coordinates, \({\bf r_{j}}\) in terms of the center of its host particle, \({\bf R}_J\), as \({\bf r}_{j'} \equiv {\bf r}_j + {\bf R}_J\). This gives:
\begin{align} \label{eq:sansS} \dfrac{d\sigma}{d\Omega}\biggr|_{\rm nucl.\, coh.\, el.} &= \biggr|\displaystyle\sum_{j'} b_{j'} \exp(i {\mathbf q} \cdot {\mathbf r}_{j'})\biggr|^2 \\ &= \biggr|\displaystyle\sum_{j,J} b_j \exp(i {\mathbf q} \cdot ({\mathbf R}_J + {\mathbf r}_j))\biggr|^2 \nonumber \\ &= \biggr|\displaystyle\sum_{J} \exp(i {\mathbf q} \cdot {\mathbf R}_J) \biggr|^2 \biggr| \displaystyle\sum_j b_j \exp(i {\mathbf q} \cdot {\mathbf r}_j) \biggr|^2 \nonumber \\ &\equiv N S({\mathbf q}) \biggr| \displaystyle\sum_j b_j \exp(i {\mathbf q} \cdot {\mathbf r}_j) \biggr|^2 , \nonumber \end{align}
where \(S({\bf q})\) is called the structure factor. For random, dilute systems, the relative phase between scattering from the particles, \(\exp(i {\bf q} \cdot ({\bf R}_J - {\bf R}_{K}))\), takes a random value. Hence, the interference vanishes on average, leading to \(S({\bf q})=1\). The derivation is left as an exercise to the reader, see Problem: The structure factor for dilute systems. With \(S({\bf q})\) known, the cross section from the scattering patterns is thus seen to be directly proportional to that from the individual particles.
In practice, the particles are often dispersed in a solution, which will also scatter the neutrons. This case is treated in the section SANS from particles in solution.
The small-angle approximation
We will here only consider scattering vectors of sufficiently small length, \(q\), so that the phase of the exponential, \(\bf q \cdot {\bf r}_j\), does not vary significantly between neighbouring atoms. The condition for this is
\begin{equation}\label{dummy1505234248} q a \ll 2\pi ,\, \end{equation}
where \(a\) is a typical interatomic distance. For larger values of \(q\), we are in a regime where the crystalline structure of the sample is responsible for the scattering. This leads to diffraction as will be explained in detail on the page on Diffraction from crystals.
Studying equation \eqref{eq:sansS}, we see that when the phase factor \({\bf q}\cdot {\bf r}_j\) varies insignificantly between neighbouring nuclei, the scattering from the individual nuclei cannot be distinguished, and the sample scatters approximately as a continuum. Hence it becomes valid to transform the sum in equation \eqref{eq:sansS} into an integral
\begin{equation}\label{eq:sans_sum} \displaystyle\sum_j b_j \exp(i \mathbf q \cdot {\mathbf r}_j) \longrightarrow \displaystyle\int_V \rho_b \exp(i \mathbf q \cdot {\mathbf r}) dV , \end{equation}
where \(\rho_b\) is the effective scattering length density for the sample. The scattering length density is defined as the sum of the coherent scattering lengths over all atoms within a given volume, \(V_0\), divided by this volume,
\begin{equation}\label{eq:rho} \rho_b = \dfrac{1}{V_0} \displaystyle\sum_{j \in V_0} b_{j} , \end{equation}
where \(j\) represents the position of the nuclei in the volume (which could be a formula unit). After the transformation, the SANS cross section reads
\begin{equation}\label{eq:SANS_cross} \dfrac{d\sigma}{d\Omega} \biggr|_{\rm SANS} = N S({\mathbf q}) \left| \displaystyle\int \rho_b({\mathbf r}) \exp(i \mathbf q \cdot {\mathbf r}) dV \right|^2 . \end{equation}
Experimental considerations
In a typical SANS experiment \(q\leq q_{\rm max} = \leq 0.3\) Å\(^{-1}\). Hence, only structures larger than around \(2\pi /q_{max}\approx 20\) Å are well resolved.
Instruments specialized in SANS can also be used to study periodic (crystalline) arrangements where the period is larger than the typical 2-10 Å, known from simple crystal structures. This could be crystals of very large molecules, superstructures, magnetic structures with long repetition length, etc.
SANS from particles in solution
One of the main applications of SANS is the study of nano-sized objects, suspended in a solution. In practice, the objects could be polymers or micelles, described in the Applications of SANS in nanoscience section, and the solvent could be water or an organic liquid.
As a start, we first consider one single nano-sized particle. For the combined system, it is convenient to separate the volume integration into an integral over the particle and an integral over the solvent,
\begin{equation}\label{dummy776960957} \dfrac{d\sigma}{d\Omega} \biggr|_{\rm SANS,\, 1\, particle} = \left| \displaystyle\int_{\rm particle} \rho_b({\mathbf r}) \exp(i \mathbf q \cdot {\mathbf r}) dV + \rho_s \displaystyle\int_{\rm solvent} \exp(i \mathbf q \cdot {\mathbf r}) dV\right|^2 . \end{equation}
By using the scattering length density contrast,
\begin{equation}\label{dummy1510031759} \Delta\rho({\mathbf r}) = \rho_b({\mathbf r}) - \rho_s, \end{equation}
the solvent integration is replaced by an integration over the entire sample volume, \(V_{\rm s}\),
\begin{equation}\label{dummy671100274} \dfrac{d\sigma}{d\Omega}\biggr|_{\rm SANS,\, 1\, particle} = \left| \displaystyle\int_{\rm particle} \Delta\rho({\mathbf r}) \exp(i \mathbf q \cdot {\mathbf r}) dV + \rho_s \displaystyle\int_{V_{\rm s}} \exp(i \mathbf q \cdot {\mathbf r}) dV\right|^2 . \end{equation}
Typically, the sample dimensions are of the order mm. This is roughly 4-6 orders of magnitude larger than the length scale of typical nano-sized particles. Hence, the contribution to small-angle scattering from the entire volume \(V\) is almost a \(\delta\)-function in \(q\) - or to be more accurate has a width of the order \(10^{-6}\) Å\(^{-1}\). Such low \(q\)-values are not at all visible in the SANS measurements, where the typical minimum scattering vector is \(q_{min} \approx 10^{-3}\) Å\(^{-1}\). We can therefore neglect the total volume scattering. Taking into account that the sample consists of \(N\) particles, the scattering cross section reads
\begin{equation}\label{dummy177978770} \dfrac{d\sigma}{d\Omega} \biggr|_{\rm SANS,\, particles} = N S({\mathbf q}) \left| \displaystyle\int_{\rm particle} \Delta\rho({\mathbf r}) \exp(i \mathbf q \cdot {\mathbf r}) dV \right|^2 . \end{equation}
Notice that the scattering cross section depends essentially on the square of the contrast in scattering length density. Hence, the scattered intensity can be changed strongly by, e.g., varying the scattering length density of the solvent. This is typically done by deuteration, as illustrated in the "five reasons" figure on the Introduction to neutron scattering page.
In a different formulation, we describe the scattering in terms of the particle density \(n = N/V_{\rm s}\) and the volume specific cross section \(\Sigma = \sigma / V_{\rm s}\). The volume specific differential scattering cross section then becomes
\begin{equation}\label{eq:SANScross} \dfrac{d\Sigma}{d\Omega} \biggr|_{\rm SANS,\, particles} = n S({\mathbf q}) \left| \displaystyle\int_{\rm particle} \Delta\rho({\mathbf r}) \exp(i \mathbf q \cdot {\mathbf r}) dV \right|^2 . \end{equation}
The particle form factor

For monodisperse, homogeneous particles, the cross section equation \eqref{eq:SANScross} simplifies to
\begin{equation}\label{dummy497150881} \dfrac{d\Sigma}{d\Omega} \biggr|_{\rm SANS,\, simple} = n \Delta\rho^2 S({\mathbf q}) \left| \displaystyle\int_{\rm particle} \exp(i \mathbf q \cdot {\mathbf r}) dV \right|^2 , \end{equation}
leading to
\begin{equation}\label{eq:SANScross2} \dfrac{d\Sigma}{d\Omega} \biggr|_{\rm SANS,\, simple} \equiv n \Delta\rho^2 V^2 S({\mathbf q}) P(\mathbf q), \end{equation}
where \(V\) is the particle volume and \(P(\mathbf q)\) is known as the particle form factor,
\begin{equation}\label{eq:sans_formfactor} P(\mathbf q)= \left| \dfrac{1}{V} \displaystyle\int dV e^{i \mathbf q \cdot {\mathbf r}} \right|^2 , \end{equation}
which takes its maximum value of 1 as \(q \rightarrow 0\).
When defining the particle volume fraction as \(\phi=NV/V_{\rm s} = nV\), the cross section reads
\begin{equation}\label{eq:SANScross_phi} \dfrac{d\Sigma}{d\Omega} \biggr|_{\rm SANS,\, simple} \equiv \phi \Delta\rho^2 V S({\mathbf q}) P({\mathbf q}). \end{equation}
Sometimes in the SANS literature, the volume specific cross section is denoted loosely \(I(\mathbf q) = d\Sigma/d\Omega\), as if it was the observed intensity.
The form factor of a solid sphere
For a solid sphere of radius \(R\), the form factor is isotropic and is easily calculated (see the problem Scattering form factor for spheres). The result is
\begin{equation}\label{eq:sans_spheres} P_{\rm sphere}(q)= \left( 3 \, \dfrac{\sin(q R)-q R \cos(q R)} {(q R)^3}\right)^2 , \end{equation} which is illustrated for different radii in Figure xx--CrossReference--fig:solidsphereformfactor--xx.
The form factor of a spherical shell
From the calculations leading to the form factor for a sphere \eqref{eq:sans_spheres}, it is straight-forward to show that the form factor amplitude for a thin spherical shell is:
\begin{equation} \label{eq:shell_form} P_{\rm shell}(q) = \left( \frac{\frac{4\pi}{3}R_{\rm out}^3P_{\rm sphere}(qR_{\rm out})-\frac{4\pi}{3}R_{\rm in}^3 P_{\rm sphere}(qR_{\rm in})}{\frac{4\pi}{3}(R_{\rm out}^3-R_{\rm in}^3)} \right)^2 , \end{equation}
where \(R_{\rm out}\) is the outer radius of the shell and the inner radius of the shell is \(R_{\rm in}=R_{\rm out} -D\), and \(D\) is the thickness of the shell. There, \(P_{\rm sphere}(qr)\) is here the form factor of a sphere \eqref{eq:sans_spheres}, as calculated in Scattering form factor for spheres.
The calculation leading to this result comes directly by expanding \eqref{eq:sans_formfactor}, using \eqref{eq:debye},
\begin{align} P(\mathbf q) &= \left| \frac{1}{V} \int dV e^{i \mathbf q \cdot {\bf r}} \right|^2 = \frac{(4\pi)^2}{V^2} \left| \int_{R_{\rm in}}^{R_{\rm out}} r^2 \frac{\sin(qr)}{qr} dr \right|^2 \nonumber \\ &= \left( \frac{3}{q^3 (R_{\rm out}^3-R_{\rm in}^3)} \right)^2 \left| \int_{qR_{\rm in}}^{qR_{\rm out}} (rq) \sin(rq) d(rq) \right|^2 \nonumber \\ &= \left( \frac{R_{\rm out}^3 P_{\rm sphere}(qR_{\rm out}) - R_{\rm in}^3 P_{\rm sphere}(qR_{\rm in})}{R_{\rm out}^3 - R_{\rm in}^3} \right)^2 . \end{align}
Polydispersity
Above, we have considered monodisperse (identical) particles only. If, however, the particles in the thin solution are not all the same size, we denote them polydisperse, and we ascribe them a size distribution, \(D(R)\), defined as the probability of finding a particle of size \(R\). Since \(D(R)\) is a probability, \(\int D(R) dR = 1\). For dilute, polydisperse particles, the form factor in equation \eqref{eq:sans_formfactor} is modified according to
\begin{equation}\label{dummy961841526} P(q)=\displaystyle\int {\rm d} R\ D(R)\ P(q,R) . \end{equation}
Hence the total SANS cross section per sample volume is
\begin{equation}\label{dummy1724599799} \dfrac{d\Sigma}{d\Omega}(q)=n (\Delta \rho)^2 \displaystyle\int {\rm d} R\ V(R)\ D(R)\ P(q,R) , \end{equation}
where \(P(q,R)\) is the size-dependent form factor and \(V(R) = (4\pi/3)R^3\).
One of the most simple - but not generally the most correct - ways of including the structure factor is by using the so-called locally monodisperse approximation [1], where we approximate the particle volume, \(V(R)\), by its average value, \(V=(4\pi/3) R_{\rm av}^3\), to reach
\begin{equation} \label{dummy17245997994342412} \frac{d\Sigma}{d\Omega}(q)=n V (\Delta \rho)^2 \int {\rm d} R \ D(R)\ P(q,R) , \end{equation}
As the concentration of particles increases, the inter-particle interaction becomes increasingly important. Hence, the structure factor \(S(q,R)\) can no longer be considered to be unity. The total SANS cross section per sample volume can then be written
\begin{equation} \label{eq:local_mono} \dfrac{d\Sigma}{d\Omega}(q)=n V (\Delta \rho)^2 \displaystyle\int {\rm d} R\ D(R) P(q,R) S(q,R) . \end{equation}
The effect of polydispersity will be explored in the problem Polydisperse spheres.
Complementarity of neutrons and X-rays
SANS is often used in combination with its sister technique, Small-Angle X-ray Scattering (SAXS), and the fundamental theories for SANS and SAXS are very similar. In addition, the experimental setup of a SAXS instrument is in principle very similar to that of the SANS instrument. The main difference between the two methods is that in SANS, the incoming neutrons are scattered by the nuclei of the studied sample, whereas in SAXS the incoming photons are scattered by the electrons.
The scattering length of an electron, \(b_{\rm e}\) is given by the classical electron radius (also known as the Compton radius or the Thompson scattering length). It is given by \(b_{\rm e}= r_0 = e^2/(4 \pi \varepsilon_0 m_{\rm e} c^2)= 2.82\) fm, where \(\varepsilon_0\) is the vacuum permittivity, \(e\) and \(m_{\rm e}\) are the charge and mass of the electron, and \(c\) is the speed of light. Thus the scattering length of an atom with atomic number \(Z\) is simply \(Z b_{\rm e}\).
SAXS has a major advantage in the easy access to very intense, well-collimated and well-focused X-ray beams, both in home-based laboratories and at large scale synchrotron facilities.
As mentioned on the Introduction page, the major advantage of SANS as compared to SAXS is the access to contrast variation via the exploitation of the difference in scattering length between hydrogen (H) and deuterium (D). This opens up for systematic contrast variation SANS measurements, where domains of specific interest in the system under investigation are enhanced at the same time as other domains are made practically invisible. This opportunity is widely applied within the investigation of biological and other organic materials. The contrast variation SANS approach has been used for investigating the internal organization of large protein complexes, to determine the finer details of phospholipid membranes, and to obtain insight into the conformation of the single polymer-chains in soft condensed materials.
Useful model-free approximations in SANS
We here present a number of useful approximations and limiting cases for small and large values of the scattering vector, \(q\). These approximations are important for the analysis and understanding of SANS data.
The Debye formula
For a randomly oriented particle of general shape, Debye was able to show a highly useful expression for the average value of the complex phase
\begin{equation} \label{eq:debye} \left\langle \exp(i {\mathbf q}\cdot{\mathbf r}) \right\rangle = \dfrac{\sin(qr)}{qr}. \end{equation}
This formula is often used for calculating the form factor of particles in solution; the proof is sketched below.
Consider a \({\bf q}\), fixed in the laboratory system, and let us define the \(z\) axis along \({\bf q}\). We consider the particles fixed in space and randomly oriented. Hence, the position, \(\bf r\), of one particular nucleus can be found anywhere on a sphere of radius \(r\), described by the spherical coordinates, \((\theta, \phi)\). We can now write \({\bf q}\cdot{\bf r} = q r \cos(\theta)\). The average value of the complex exponential function is given by the spherical integral
\begin{equation}\label{dummy25288786} \left\langle \exp(i {\mathbf q}\cdot{\mathbf r}) \right\rangle = \dfrac{1}{4\pi} \displaystyle\int d\theta d\phi \sin(\theta) \exp(i {\mathbf q}\cdot{\mathbf r}) = \dfrac{1}{2} \displaystyle\int_0^\pi d(\cos\theta) \exp(i qr \cos\theta) = \dfrac{\sin(qr)}{qr} . \end{equation}
The Guinier approximation
We will now present an important approximation for particle structure factors in small-angle scattering. Here, we show the Guinier approximation for small values of \(q\).
Let us first study the hard-sphere form factor equation \eqref{eq:sans_spheres} for small values of \(q\), e.g. \(q R \ll 1\). We expand the trigonometric functions to 5th(!) order in \(q R\), reaching
\begin{equation}\label{eq:sphereguinier} P_{\rm sphere}(q) \approx 1-\dfrac{1}{5}(q R)^2 .\, \end{equation}
This function has the same series expansion (to second order) as the expression \(\exp(-(q R)^2/5)\), which is what we define as the Guinier approximation for the sphere form factor.
To generalize from this example, we can cast the equation in terms of the radius of gyration. The radius of gyration of the sphere is easily calculated by converting \eqref{eq_rg} into an integral, reaching
\begin{equation} \label{eq:Rg_sphere} R_{\rm g}^2 = 3 R^2 / 5 . \end{equation}
This leads to
\begin{equation}\label{eq:guinier} P(q) \approx \exp\left(-\dfrac{1}{3}(q R_{\rm g})^2\right) . \end{equation}
In fact, this is the general Guinier approximation valid for any particle shape. We will, however, not show it in the general case here.
The Porod law
We here present the important Porod law, which is valid for large \(q\) values.
We again consider the sphere form factor equation \eqref{eq:sans_spheres}, this time for large values of \(q\), e.g. \(q R \gg 2 \pi\). To leading value of \(q R\), this becomes
\begin{equation}\label{dummy994030239} P_{\rm spheres}(q) \approx \dfrac{9 \cos^2(q R)}{(q R)^{4}} . \end{equation}
Now, for large \(q\), even very small variations in the particle size, \(R\), will lead to a variation of the cosine argument \((q R)\) by an amount comparable to, or larger than, \(2\pi\). For such a sample, we will observe approximately the average value of the cosine, i.e., \(\left\langle \cos^2(q R) \right\rangle = 1/2\), leading to \(P(q) \approx 9/(2q^4R^4)\) or
\begin{equation}\label{eq:porod} P(q) \propto q^{-4} .\, \end{equation}
This is, in fact, the generally valid Porod law for small-angle scattering. We will not show the Porod law directly here. Intuitively, however, it is reasonable to generalize from the example of the spheres. Here, the real-space structure (the particle radius) probed at a scattering vector of \(q\) is of the order \(\pi/q\), as judged from the position of the first "dip" in the expression for the particle form factor. Hence, at much larger values of \(q\), the measurement is sensitive to smaller real-space structures. However, the only small real-space structures visible are sharp surfaces: The boundary between two different scattering length densities. And the reflectivity from a surface is in fact proportional to \(q^{-4}\), as will be shown in the page on Neutron reflectivity.
- ↑ J.S. Pedersen. J. Appl. Cryst. 27 (1994), p. 595-608
Small-angle scattering instruments
A small-angle scattering instrument at a continuous source
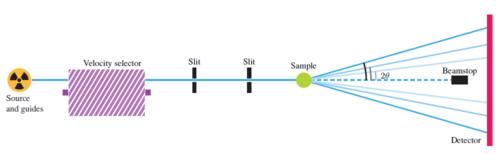
The principle of an ordinary SANS instrument is rather simple. We will here present a SANS instrument for a continuous source, although a generalization to a time-of-flight instrument is straightforward. A sketch of a SANS instrument is shown in Figure xx--CrossReference--fig:sans_instr--xx.
- Source: A SANS instrument uses neutrons from a cold moderator and is situated at the end of a guide.
- Velocity Selector: The neutrons are being monochromatized by a rotating velocity selector, letting through a wavelength band of typically \(\Delta \lambda/\lambda \approx\) 10 %.
- Collimator: The divergence of the incident neutrons is limited by a pair of pinhole, that acts as a collimator. Often, one can control the pinhole diameter and their distance, the collimation length, \(L_{\rm c}\), by inserting different pinholes at a number of fixed positions. The smallest collimation length is typically 1 m, while the longest varies between 5 m and 20 m, depending on the particular instrument.
- Sample: The sample is often flat and mounted perpendicular to the beam direction, so that all neutrons scattered at small angles will penetrate the full sample thickness. Hence, samples are often thin to limit absorption and multiple scattering.
- Detector: The neutrons are detected by a position-sensitive detector (PSD), which can determine the position of an incident neutron, placed at a distance \(L_{\rm d}\) from the sample. A typical PSD is \(1 \times 1\) m\(^2\) with a precision in positioning of 1-5 mm. The PSD is placed within an evacuated tank to avoid air scattering (which is mainly due to nitrogen), and the sample-detector distance can be varied by moving the PSD within the tank. The minimum PSD distance is around 1 m, while the maximum distance varies in the range 5-20 m determined by the length of the tank. Typically, one would match the sample-detector distance to the collimation length.
- Beam stop: An absorbing beam-stop is placed in the direct beam just before the detector to limit the number of neutrons from the direct beam. This strong beam could otherwise saturate, or even damage, the detector. For correct placing of the beamstop, it is necessary to take into account how gravity affects neutrons of different wavelengths; see the problem The effect of gravity in the Simulation project: A small angle neutron scattering instrument.
A small-angle scattering instrument at a pulsed source
At a pulsed source, a small-angle scattering instrument is very much the same for a continuous source. The only difference is that there is no velocity selector. In stead, the neutron wavelengths are determined by their respective time of flight, as discussed in Determining the incoming neutron wavelength.
← Previous page: Instrumentation
→ Exercises: Exercises in Small angle neutron scattering
→ Next page: Neutron reflectivity