Introduction to neutron scattering
Neutron scattering is one of the most powerful and versatile experimental methods to study the structure and dynamics of materials on the atomic and nanometer scale. Quoting the Nobel committee, when awarding the prize to C. Shull and B. Brockhouse in 1994 for the invention of neutron scattering, these pioneers have "helped answer the question of where atoms are and ... what atoms do".
Neutron scattering is presently used by more than 10,000 researchers worldwide, and the scope of the method is continuously broadening. In the 1950's and 1960's, neutron scattering was an exotic tool in Solid State Physics and Chemical Crystallography, but today it serves communities as diverse as Biology, Earth Sciences, Planetary Science, Engineering, Polymer Chemistry, and Cultural Heritage. In brief, neutrons are used in all scientific fields that deal with hard, soft, or biological materials.
It is, however, appropriate to issue a warning already here. Although neutron scattering is a great technique, it is also time-consuming and rare. Neutron scattering experiments last from hours to days and are performed only at a few handfuls of large international facilities. Here, access to measurement time is very competitive, and the running costs correspond to typically 10,000 Euros per instrument day. Hence, neutron scattering should be used only where more accessible methods are inadequate.
For the study of atomic and nanometer-scale structure in materials, X-ray scattering is the technique of choice. X-ray sources are by far more abundant and are, especially for synchrotron X-ray sources, much more intense than neutron sources. Hence, the rule of thumb goes: "If an experiment can be performed with X-rays, use X-rays". For an introduction to X-ray scattering, see, e.g., the excellent textbook by D. F. McMorrow and J. Als-Nielsen[1].
However, neutrons have a number of properties that make them extremely useful for purposes where X-rays are insufficient. This chapter will present these properties and describe essential differences between neutron- and X-ray-scattering.
- ↑ D. F. McMorrow and J. Als-Nielsen, Modern X-ray scattering (Wiley, 2001)
Basic properties of the neutron
The neutron is a nuclear particle with a mass, \(m_{\rm n}\), rather close to that of the proton[1]
\begin{equation}\label{dummy782923085} m_{\rm n} = 1.67493 \cdot 10^{-27} \, {\rm \,kg} . \end{equation}
The neutron does not exist naturally in free form, but decays into a proton, an electron, and an anti-neutrino. The neutron lifetime, \(\tau = 886 {\rm \,s}\)[2], is much longer than the time a neutron spends within a scattering experiment, which is merely a fraction of a second. Hence, neutron decay can typically be neglected in experiments.
The neutron is electrically neutral but still possesses a magnetic moment
\begin{equation}\label{eq:intro_moment} \mu = \gamma \mu_{\rm N} ,\, \end{equation}
where \(\gamma= - 1.91304\) is the neutron magnetogyric ratio and the nuclear magneton is given by \(\mu_{\rm N} = e \hbar / (2 m_{\rm p}) = 5.05078 \cdot 10^{-27} \,{\rm J}/{\rm T}\). The neutron magnetic moment is coupled antiparallel to its spin, which has the value \(s=1/2\).
The neutron interacts with nuclei via the strong nuclear force and with magnetic moments via the electromagnetic force. Most of this text deals with the consequences of these interactions; i.e. the scattering and absorption of neutrons by atoms and nuclei inside materials, as well as reflection from surfaces and interfaces.
Particle-wave duality
One of the remarkable consequences of quantum mechanics is that matter has both particle- and wave-like nature[1]. The neutron is no exception from this. In neutron scattering experiments, neutrons behave predominantly as particles when they are created in a nuclear process, as interfering waves when they are scattered, and again as particles when they are detected by another nuclear process.
To be more specific on the wave nature of matter, a particle moving with constant velocity, \(v\), can be ascribed a corresponding (de-Broglie) wavelength, given by
\begin{equation}\label{dummy1979310179} \lambda = \dfrac{2 \pi \hbar}{m v} . \end{equation}
In neutron scattering, the wave nature is often referred to in terms of the neutron wave number,
\begin{equation}\label{dummy1979310179321321} k = \frac{2 \pi}{\lambda} , \end{equation}
or the wave vector of length \(k\) and with same direction as the velocity:
\begin{equation}\label{eq:wavenumber} \mathbf{k} = \dfrac{m_{\rm n} \mathbf{v}}{\hbar} . \end{equation}
By tradition, wavelengths are measured in Å (\(10^{-10} {\rm \,m}\)), and wave numbers in Å\({}^{-1}\), although some groups rather tend to use nm and nm\({}^{-1}\). The neutron velocity is always measured in SI units: m/s. For our purpose we consider the neutrons as non-relativistic, and the neutron kinetic energy is given by
\begin{equation}\label{dummy1797195180} E = \dfrac{\hbar^2 k^2}{2 m_{\rm n}} , \end{equation}
which is measured in eV or meV, where \(1 {\rm eV} = 1.60218 \cdot 10^{-19} {\rm \,J}\). A useful conversion table between velocity, wave number, wavelength, energy, and temperature, is shown in Table xx--CrossReference--tab:conversion--xx[2].
Neutron scattering facilities

Neutron sources with flux densities adequate for neutron scattering investigations of materials are based on one of two principles, also illustrated in Figure xx--CrossReference--fig:production--xx:
- Fission: A high continuous flux of neutrons is produced in the core of a conventional fission reactor.
- Spallation: A pulsed production of neutrons is obtained by bombarding a target of heavy elements with high-energy particles, typically accelerated protons.
Common to both types of sources is that neutrons are moderated to "thermal" or "cold" velocities close to the source and then transported to the neutron scattering instruments in neutron guide systems. For the conventional naming of neutron energy intervals, see Table xx--CrossReference--tab:neutron_naming--xx.
Both fission and spallation neutron sources are built as dedicated facilities, each hosting tens of instruments. All major sources are user facilities, meaning that they serve a research community much larger than the staff affiliated with the facilities. Typically, user experiments are selected through a competitive proposal system.
At the time of writing, more than twenty neutron facilities are in operation worldwide. The most important being the reactor source ILL, Grenoble, France, and the spallation source ISIS, Oxfordshire, UK. However, the traditional European dominance in this field was in the late 00's challenged by the new and powerful spallation sources: Spallation Neutron Source SNS, Oak Ridge, USA, and Japan Proton Accelerator Research Complex J-PARC, Tokai, Japan. For this reason, it was in 2009 decided to build the European Spallation Source (ESS), in Lund, Sweden. After some years of preparation work, the actual construction was initiated in the summer of 2014. The source is expected to be operational in 2022, with first user experiments ultimo 2013, and to reach full power with 16 running instruments in 2028[1].
A list of the most significant neutron sources worldwide is given at the Neutron sources and moderators page.
Five reasons for using neutrons
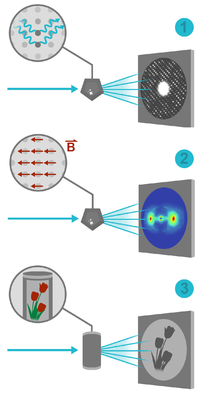
We will now present some of the assets of neutron scattering. We will focus on cases where neutrons can be preferred to X-rays or where neutrons are needed to complement X-rays. It is commonly agreed in the neutron scattering community that this can be formulated in five general points:
- Energy and wavelength: Thermal neutrons have a wavelength (around 1.8 Å) similar to inter-atomic distances, and an energy (around 25 meV) similar to elementary excitations in solids. One can thus obtain simultaneous information on the structure and dynamics of materials and e.g. measure dispersion relations (energy-wavelength dependence) of excitations in materials.
- Isotopes and light elements: The neutron scattering cross section varies in a seemingly erratic fashion between elements and even between different isotopes of the same element. The scattering cross section is sizable for all elements, and one can thus use neutrons to study light isotopes. In particular, this is important for hydrogen, which is almost invisible to X-rays. With neutrons, the large difference in scattering between usual hydrogen (\(^1\)H) and deuterium, (\(^2\)D) can be used in soft matter and life sciences to change the contrast in the scattering and also "highlight" selected groups within large molecules or aggregates.
- Quantitative experiments: The interaction between neutrons and (most) matter is rather weak, implying that neutrons can probe the bulk of the sample, and not only its surface region. The weak interaction also diminishes higher order effects, such as multiple scattering. Hence, quantitative comparisons between neutron scattering data and theoretical models can be performed to a high precision.
- Transparency: Since neutrons penetrate matter easily, neutron scattering can be performed with samples stored in all sorts of sample environment, such as cryostats, magnets, furnaces or pressure cells. Furthermore, very bulky samples can be studied, up to tens of cm thickness, depending on their elemental composition. The sample is left relatively unharmed by the neutron experiment, although beam experiments should certainly not be performed on living organisms.
- Magnetism: The neutron magnetic moment makes neutrons scatter from magnetic structures or magnetic field gradients. Normal (unpolarized) neutrons are used to learn about the periodicity and magnitude of the magnetic order, while scattering of spin-polarized neutrons can reveal the direction of the atomic magnetic moments. Also. the dynamics of the magnetic moments can be revealed.
In most cases, neutron scattering is performed in combination with other experimental techniques; often with neutron scattering as one of the final techniques to be applied before conclusions are drawn.
On these notes
After this brief introduction, we will continue the introductory part of this WIKI by presenting the formalism of the neutron scattering process (Basics of neutron scattering). In part II, we go more into details with neutron sources, moderators and guide systems (Neutron sources and moderators), as well as components for neutron optics and instruments (Instrumentation).
In the later parts, we will describe the actual applications of neutron scattering. For each case, we give the scientific motivation and the relevant corresponding description of the scientific field. We then proceed to the theory for that particular type of scattering, a score of illustrative examples on scientific use and data analysis, and a number of relevant problems.
- Part III describes the study of material structure by elastic neutron scattering or absorption. Small angle neutron scattering (SANS) is presented on the Small angle neutron scattering page, reflectometry on the Neutron reflectivity page, diffraction from crystals Diffraction from crystals, and tomography on the Imaging page.
- Part IV deals with the study of dynamics in materials by inelastic neutron scattering, in particular the study of coherent lattice vibrations (phonons) on the page Scattering from lattice vibrations.
- Part V describes elastic and inelastic scattering from magnetic materials on the Magnetic neutron scattering and Inelastic magnetic scattering pages.
The final part VI contains an introduction to neutron ray-tracing simulations, often used for instrument design and for simulating the effect of the combined geometry of neutron scattering instruments. Here, however, they are also used to form the basis for a number of working problems shaped as "virtual experiments", where the student of these notes may investigate a problem in neutron science or instrumentation by means of simulations [1].
Reading the text
The text is intended so that after the introduction in part I and part II, each part can in principle be studied independently. However, the parts IV and V rely to a minor extent on basic results from part III. Part IV forms the basis for the simulation problems, but requires only knowledge of part II.
The reader is assumed to have a general knowledge of classical physics and complex numbers for the description of waves, and a general knowledge of mathematics, corresponding to first year curriculum on most university educations in Physics, Chemistry, and Engineering. The main chapters of the text assumes very little knowledge of quantum mechanics. At places where a deeper quantum mechanical presentation could be elucidating for some students, there will be follow-up sections containing the formal derivation of the results. These sections can be omitted without essential loss of contents; they are marked by an asterisk (*).
Future extensions
In later version of this note, we aim to include a number of other utilizations of neutron scattering, like single crystal diffraction, and scattering from liquids.
More advanced topics, like a detailed account of scattering with polarized neutrons, analytical calculations of instrumental resolution, and the production and use of ultracold neutrons will be written in one or more extensions to the notes.
- ↑ K. Lefmann et al., Journal of Neutron Research, vol. 16, p. 97-111, (2008)
← Previous page: Main page
→ Next page: Basics of neutron scattering