Determining the incoming neutron wavelength

The famous Bragg law gives the relation between the wavelength, \(\lambda\), of radiation diffracting off a crystal with lattice spacing, \(d\), and the scattering angle, \(2\theta\):

\begin{equation} \label{eq:pre-bragg} n \lambda = 2 d \sin(\theta),\, \end{equation}

as presented on the Diffraction from crystals page - and derived thoroughly in the adjacent text. According to the Bragg law, in order to interpret the neutron signal at a particular angle, \(2\theta\) (meaning determine the lattice spacing, \(d\)), it is necessary to know the neutron wavelength, \(\lambda\). This is in practice done in two different ways:

• At continuous sources, the neutron beam is in general monochromatized
• At pulsed sources time-of-flight techniques are used to determine \(\lambda\).

We will here look in more detail on these two rather different methods.

Velocity selector

Figure 1: A principal sketch of a neutron velocity selector. The neutron travel left-right, and the absorbing blades of the velocity selector rotate around an axis parallel to the neutron flight path.

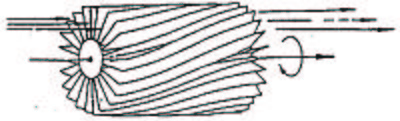
A neutron velocity selector is made from spinning absorbing blades, tilted from the main axis; see Figure xx--CrossReference--fig:velocityselector--xx. The neutron is transmitted only if its speed matches the selector rotation speed, so that the neutron never hits an absorbing blade. This arrangement will allow passage of neutrons with velocities close to a particular value; typical values are 2-20~Å , depending on selector rotation speed. The monochromatization is coarse; typically of the order of \(\Delta \lambda/\lambda \approx\)~10\%. Further details are left to the reader as an exercise, see Problem: Neutron velocity selector.

Monochromating a continuous neutron beam

To obtain a more precise determination of \(\lambda\), one uses another method: Bragg reflection from a crystal.

Consider again the Bragg law \eqref{eq:pre-bragg}, and imagine that now the lattice spacing, $d$, of the crystal is well known. In addition, the incident neutrons have a well-defined direction, but are polychromatic (a so-called white beam). In this case, only neutrons of certain wavelengths are scattered:

\begin{equation}\label{dummy291868694} \lambda = \dfrac{1}{n} 2 d \sin(\theta_{\rm m}) . \end{equation}

A crystal used in this way is called a monochromator, represented by the subscript "m" on the scattering angle \(2 \theta_{\rm m}\). The monochromator reflects a series of wavelengths, given by the integer, \(n\). The first order wavelength (\(n=1\)) is usually the desired one, while the higher order wavelengths are undesired. Typically, one will try to suppress the higher order neutrons by transmission filters and/or by guide geometries which provide low transmission for shorter wavelength neutrons.

An estimate of the monochromaticity of the diffracted beam is given by considering the uncertainty in the scattering angle, \(\delta\theta\), which is mostly determined by the experimental geometry: Guides, colllimators and slits. In contrast, the uncertainty in the lattice spacing is in many cases negligible. Performing uncertainty estimation (error propagation) of the Bragg law leads to

\begin{equation}\label{dummy2061579416} \delta\lambda = \dfrac{1}{n} 2 d \cos(\theta_{\rm m}) \delta\theta , \end{equation}

when \(\theta\) is calculated in radians. One often considers the relative precision of the wavelength determination:

\begin{equation}\label{dummy2099421147} \dfrac{\delta\lambda}{ \lambda} = \cot(\theta_{\rm m}) \delta\theta . \end{equation}

For \(90^\circ\) scattering (\(\theta = 45^\circ\)) and a typical divergence value \(\delta\theta = 0.5^\circ\), we reach \(\delta \lambda / \lambda \approx 1\) %.

Monochromators for thermal neutrons are often made from single crystals of Si, Ge, or Cu. For cold neutrons, pyrolytic graphite (PG) is the material of choice. As with most other large single crystals, monochromator materials often consist of many crystallites, which have a small, random misalignment with respect to a "common" direction. This mosaicity is often close to being Gaussian (i.e. a normal distribution) and affects the monochromatizing properties of the material strongly. A small mosaicity (10'-20') reflects a smaller amount of the incoming neutrons than larger mosaicities (30'-60'). On the other hand, a small mosaicity is beneficial if one requires a good resolution, i.e. a narrow wavelength distribution of the beam.

Experimental considerations

Monochromators for thermal neutrons are often made from single crystals of Si, Ge, or Cu. For cold neutrons, pyrolytic graphite (PG) is the material of choice.

Reflectivities of monochromators in Bragg condition depend both on the chosen material and on the neutron wavelength. Typical values range from 20 % to 80 %; the latter value achieved by PG with neutrons of \(\lambda > 4\) Å.

Time-of-flight analysis

Figure 2: Time-of-flight diagram for a typical diffraction experiment. The horizontal axis denote time, \(t\), where the initial pulses begin at \(0, T, 2T\), etc. The vertical \(x\)-axis denote the position along the main axis of the instrument, where PS is the pulse shaping chopper, FO is the frame overlap chopper (that here also functions as bandwidth definition chopper), S the sample, and D the detector. Each neutron follows one path in the time-of-flight diagram, depending on its emission time and its velocity/wavelength; the shaded areas represent the continuum of allowed paths. At the moderator, a broad wavelength band is emitted, corresponding to a large spread in slopes in the \((x,t)\) diagram. The PS and FO choppers select a certain wavelength interval, which is narrow enough to avoid frame overlap (overlap between neutrons from different pulses at the detector).

A completely different method of determining the neutron wavelength is by measuring the speed of the particle by time-of-flight analysis. Typical moderators at pulsed sources emit bursts of neutrons lasting \(\tau = 10-100\) \(\mu\)s separated by intervals of \(T \approx 20-100\) ms. The neutron start time at the moderator is thus very well defined. The neutron flight time from the moderator to the detector placed a distance, \(L\), from the moderator is

\begin{equation}\label{eq:TOF} t = \dfrac{L}{v} =\dfrac{m_{\rm N}}{2 \pi \hbar} L \lambda = \alpha \, L \, \lambda , \end{equation}

where \(\alpha = m_{\rm n}/h = 252.7\, \mu\) s/m/Å. The neutron wavelength can thus be determined directly from its time-of-flight. The uncertainty in the wavelength is in practice given by the pulse width \(\tau\) through

\begin{equation}\label{dummy133888562} \alpha L \delta \lambda \approx dt = \tau , \end{equation}

leading to

\begin{equation}\label{dummy954736455} \dfrac{\delta \lambda}{\lambda} = \dfrac{\tau}{\alpha L \lambda}. \end{equation}

Hence, to have a good relative wavelength resolution, one would use a long instrument (large \(L\)), use a source with a short pulse length \(\tau\), and/or use a long wavelength.

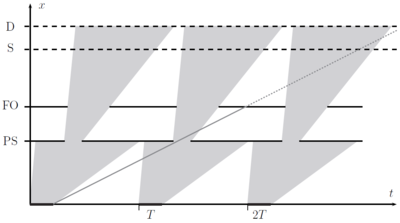
In diffraction experiments, one typically allows a broad wavelength band from the incident beam to hit the sample, and later determine the wavelength of the detected neutrons from the time-of-flight at the (time-sensitive) detectors. The reason for not allowing the full white beam in the incident beam is to avoid frame overlap. This happens when the slow neutrons from one pulse are overtaken by fast neutrons from the following pulse, creating ambigiuity in the data analysis. This is best illustrated on a time-of-flight diagram; see Figure xx--CrossReference--fig:TOF--xx. The spread in arrival times, \(\Delta t\), cannot be allowed to exceed the time between pulses, \(T\). From equation \eqref{eq:TOF}, the wavelength spread, \(\Delta \lambda\) is limited by

\begin{equation}\label{dummy1580353440} \alpha L \Delta \lambda < T . \end{equation}

The (broad) wavelength band is usually limited by disk choppers, which are in this connection denoted bandwidth definition choppers. Similar choppers are placed slightly longer downstream to prevent very slow neutrons from entering the bandwidth chopper from a wrong source pulse. Such choppers are called frame overlap choppers.

It is possible by fast spinning choppers to define a (nearly) monochromatic neutron beam from a pulsed source. This is used for inelastic neutron scattering and will be discussed later.

The ESS will have a very long pulse, \(\tau = 2.86\) ms. Hence, standard logic for pulsed sources does not apply, and many instrument concepts must be re-considered.

In particular, a shaping (shortening) of the pulse by choppers close the moderator is necessary for many instruments to avoid too large uncertainties in the determined value of \(\lambda\).