Problem:Scattering form factor for spheres

A sample of dilute, identical spheres with radius \(R\) dispersed in a solvent will scatter uniformly with the form factor

\( P_\text{sphere}(q) = \left( 3 \dfrac{\sin{(qR) - qR \cos{(qR)}}}{(qR)^3} \right)^2 . \)

Question 1

Show by direct integrations that this form is correct.

Hint

Use spherical coordinates or the Debye formula (this equation on the SANS page).

Solution

\(V=4 \pi R^3 /3\) and \(\mathbf{q}\cdot\mathbf{r}=qr\cos(\theta)\). In spherical coordinates the volume element is \(dV=r^2\sin{\theta}\rm{d}r \rm{d}\theta\rm{d}\phi\).

\( \begin{align*} \dfrac{1}{V}\displaystyle\int\rm{d}V e^{-i\mathbf{q}\cdot\mathbf{r}} &= \dfrac{3}{4\pi R^3}\displaystyle\int^{2\pi}_0 \rm{d}\phi\displaystyle\int^{\pi}_0\rm{d}\theta \displaystyle\int^{R}_0\rm{d}r \quad r^2\sin{\theta}e^{-iqr\cos{\theta}}\\ &= \dfrac{3}{2 R^3}\displaystyle\int^{R}_0\rm{d}r \quad r^2 \displaystyle\int^{\cos{\theta}=1}_{\cos{\theta}=-1}\rm{d}(\cos{\theta}) e^{-iqr\cos{\theta}}\\ &= \dfrac{3}{2R^3}\displaystyle\int^{R}_0\rm{d}r \quad r^2\left(\dfrac{e^{-iqr}-e^{iqr}}{-iqr}\right)\\ &= \dfrac{3}{R^3}\displaystyle\int^{R}_0\rm{d}r \quad r^2\left(\dfrac{\sin(qr)}{qr}\right)\\ &= \dfrac{3}{qR^3}\displaystyle\int^{R}_0\rm{d}r \quad r \sin(qr) \\ &= \dfrac{3}{qR^3}\left[\dfrac{-r\cos(qr)}{q}\right]^R_0 + \displaystyle\int^{R}_0\rm{d}r \quad \dfrac{\cos(qr)}{q}\\ &= \dfrac{3}{qR^3}\left( \dfrac{-R\cos(qR)}{q}+ \dfrac{\sin(qR)}{q^2}\right)\\ &= 3\dfrac{\left(\sin(qR)-qR\cos(qR \right)}{(qR)^3} . \end{align*} \)

Hence

\( P_{\rm sphere}(q) = \left| \dfrac{1}{V}\displaystyle\int\rm{d}V e^{-i\mathbf{q}\cdot\mathbf{r}} \right|^2 = \left( 3\dfrac{\left(\sin{qR}-qR\cos{qR} \right)}{(qR)^3}\right)^2 , \)

where \(P\to 1\) for \(q\to 0\).

The total intensity from a particle of volume \(V[\)Å\(^3=10^{-24}\text{cm}^3]\) in a solvent giving the excess scattering length \(\Delta \rho \,[{\rm fm}/ \)Å\(^3] =0.1[{\rm cm}/{\rm{cm}^3}]\) is

\( I(q)=\phi V (\Delta \rho)^2 P .\, \)

Question 2

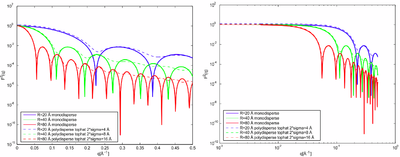
Implement the obtained form factor in MatLab or a similar program and calculate and plot the form factor for spheres with radii, \(R=20\) Å, \(R=40\) Å, and \(R=80\) Å as a function of \(q\).

Question 3

Plot the form factor and observe the smearing due to a polydispersity if there is an uncertainty in these radii of the magnitude \(\Delta R/R = 10\) % (assume a uniform distribution of sizes in the range \([R-\Delta R ; R + \Delta R]\)).

Solution

Figure 1: The form factor for hard spheres on logarithmic scale. Solid curves are for monodisperse particles of one size, dashed curves are for tophat particle distributions with a \(\pm\) deviation 10 % of the mean particle size. The left figure shows the scattering vector \(q\) on a linear scale, the right figure is on a logarithmic scale.

If the particles in the solution are not all the same size, the form factor is modified according to the size distribution \(D(R)\) by

\( P(q)=\displaystyle\int {\rm d} R\ D(R)\ F^2(q,R) . \)

The scattered intensity (volume specific cross-section) from a distribution of spheres with sizes \(D(R)\) is hence

\( I(q)=\phi V (\Delta \rho)^2 \displaystyle\int {\rm d} R\ D(R)\ F^2(q,R) , \)

where \(F(q,R)\) is the form factor amplitude for spheres in this case.

The form factor for 20, 40 and 80 Å particles is shown in Figure xx--CrossReference--fig:formfactor_spheres--xx, ( the same as the volumespecific cross-section assuming \(\phi V (\Delta \rho)^2=1\) ). Also shown is the smearing of the ripples due to 10 % polydispersivity.