Powder scattering instruments

We will here present typical lay-out of powder scattering instruments for continuous and pulsed sources, respectively.

A powder diffractometer at a continuous source

Figure 1: Schematic lay-out of the typical high-resolution thermal powder diffractometer HRPT at SINQ, PSI. From the moderator (top left), the beam is monochromatized by Bragg scattering from a crystal, then passing a collimator and a slit before hitting the sample (green). The multidetector (red) simultaneously captures neutrons scattered over a wide angular range. A radial collimator (grey) limits the part of the background that does not originate from the sample.

Figure 2: Picture of the multidetector for the HRPT powder diffractometer at PSI (white-blue) and its monochromator shielding (red).

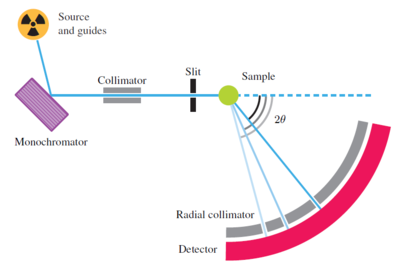
A typical continuous-source powder diffractometer, the HRPT instrument at PSI, is illustrated in Figure xx--CrossReference--fig:HRPT1--xx and Figure xx--CrossReference--fig:HRPT2--xx. The instrument bears much resemblance to the two-axis diffractometer shown in the introduction to this chapter:

• Source: The diffractometer uses a beam of thermal neutrons straight from a beam port without use of neutron guides.

• Monochromator: The beam is diffracted by a monochromator (see Determining the incoming neutron wavelength), which selects the neutron wavelength, typically in the range 1-2~\AA .

• Collimator: The monochromatic beam then passes through a narrow horizontal Soller collimator.

• Sample: The low-divergent, monochromatic beam hits the powder sample, which is often situated in a vacuum environment to reduce background from air scattering. In the sample, the neutrons are scattered according to Bragg's law, see Diffraction from crystals.

• Detector: The scattered neutrons are detected by a large arc-shaped detector bank, with typically hundreds of channels, each covering a narrow range of the scattering angle, \(2\theta\). The detectors have a limited height (perhaps 10-20~cm), to avoid a smearing effect in the data, caused by the blur in total scattering angle when the out-of-plane component is significant.
• Radial collimator: Background neutrons flying around in the sample-detector area are suppressed by a radial collimator between sample and detector. \\

Figure 3: A typical powder diffraction pattern, taken by the TAS3 diffractometer at Risø (now placed at Kjeller(N)), which has a similar construction as HRPT. (left) The raw data shown as count vs. scattering angle, \(2\theta\). (right) The data as counts vs. scattering vector, \(q\).

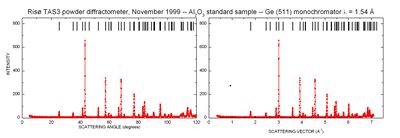
A typical set of powder diffraction data is given in Figure xx--CrossReference--fig:powderdata--xx. Both the raw data and the data converted into scattering vector is shown. The background value between the peaks is mostly elastic incoherent scattering from the sample, but also thermal diffuse scattering contributes at larger scattering angles; see Scattering from lattice vibrations. Towards low scattering angles, there is an increased background due to small-angle scattering of the direct beam.

As can be clearly seen, the resolution of the diffractometer (the width of the powder peaks) varies with scattering angle. In particular, the peaks are broadest at high scattering angles. This effect is well understood, but we will not go into details with it here.

A powder diffractometer at a pulsed source

In a time-of-flight diffraction experiment, the neutron wavelength will change with time, with the shortest wavelength arriving earliest. Hence, at a typical moment in time, there will be Bragg scattering from several lattice spacings. However, the scattering angle from any given reflection will increase with time as the wavelength increases.

To maximize count rate, a typical powder diffractometer is equipped with a large number of time- and position-sensitive detectors that cover a significant fraction of the \(4\pi\) solid angle. The typical raw data from a time-of-flight powder diffraction experiment will be (transformed to be) two-dimensional: Neutron counts vs. flight time, \(t\), and detector angle, \(2\theta\). In such a plot, powder lines will be seen as connected curves through \((2\theta,t)\) space. The processed data will contain only neutron intensity vs. \(q\) (or vs. lattice spacing, \(d\)), probably normalized in proper units of cross section.

The presently most powerful time-of-flight diffractometer is named GEM, and is placed at the 50 Hz source ISIS (UK). With this instrument, a complete powder diffraction pattern can be recorded within a single pulse (lasting 10-15 ms). In this way, it is possible to monitor diffraction signals from fast processes in real time, e.g. chemical reactions.