Spectrometers: Instruments for inelastic neutron scattering
On instruments that use a continuous beam of neutrons, it is necessary to directly select both \(E_{\rm i}\) and \(E_{\rm f}\), in order to determine the neutron energy transfer, \(\hbar\omega\). It is here customary to use Bragg diffraction from crystals for both purposes. Such a type of instrument is denoted a triple-axis spectrometer, since the neutron changes direction by scattering three times before being detected:
- A monochromator crystal selects \(E_{\rm i}\) of the incoming beam, as discussed in Determining the incoming neutron wavelength, by Bragg scattering an angle \(2\theta_{\rm m}\).
- The sample scatters the beam by the angle \(2\theta\).
- The analyzer determines \(E_{\rm f}\) by Bragg scattering by an angle \(2\theta_{\rm a}\), in the same way as the monochromator.
The path of the neutron beam is kept in the same horizontal plane, also denoted the scattering plane. The build-up of the triple-axis spectrometer is shown in Figure xx--CrossReference--fig:tripleaxisspectrometer--xx, and the individual components of the spectrometer are listed below:
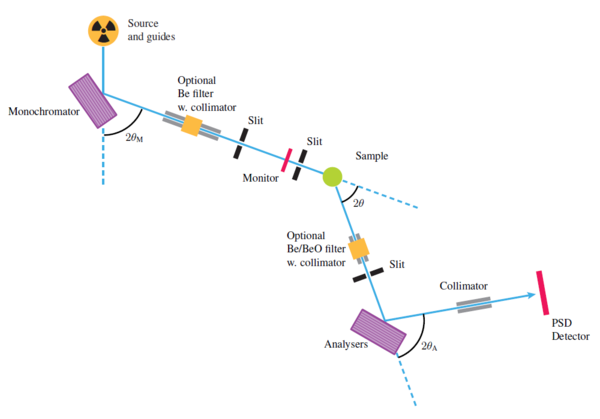
Source
The triple axis spectrometer uses a beam of cold or thermal neutrons. Most usually, a neutron guide is used to transport the beam to areas far from the source where the stray background is lower.
Monochromator
The beam is diffracted by a monochromator (see subsection Determining the incoming neutron wavelength), which selects the neutron energy, \(E_{\rm i}\), typically in the range 14-100~meV at a thermal moderator, or 2.5-14~meV for a cold moderator.
Filter
The monochromatised beam is almost always polluted with higher order scattering, from \(n>1\) in Bragg's law. A filter is used to remove these higher order scattered neutrons, either before or after the sample, or in both places.
Collimator
The monochromatic beam passes through a (often loosely collimating) horizontal Soller collimator. Collimators may also be inserted before the monochromator (rarely), between sample and analyzer (often), and after the analyzer (sometimes).
Sample
The medium-divergent, monochromatic beam hits the sample, which is often one (or several co-aligned) single crystal situated in a vacuum environment to reduce background from air scattering. In the sample, the neutrons are scattered elastically and inelastically.
Analyser
The scattered beam is again monochromatized by the analyser crystal, which works just like a monochromator, just selecting the final neutron energy, \(E_{\rm f}\). Usually, pyrolytic graphite is used for analyzer material.
Detector
The scattered neutrons are eventually detected by a single detector. This means that data on a triple-axis spectrometer are taken point by point. More advanced spectrometers may have several analyzer-detector arrangements, allowing for simultaneously detecting several points in \(({\bf q},\omega)\)-space. [1][2][3]
By correct selection of the three scattering angles, and the sample rotation, \(\omega_{\rm s}\), around a vertical axis,
the triple-axis spectrometer can be adjusted to any value of
scattering vector, \({\bf q}\), and energy transfer, \(\hbar \omega\),
allowed by the scattering condition (\ref{eq:inelastic_basic}).
In fact, \({\bf q}\) can only obtain values within the scattering plane.
This means that there are 4 free angles to determine only 3 parameters:
\(\hbar \omega\) and 2 dimensions of \({\bf q}\). In practice, this ambigiuity
is solved by fixing either \(E_{\rm i}\) or \(E_{\rm f}\) to a predetermined value.
A thorough presentation of how to perform experiments with a triple-axis spectrometer is given in Ref.~\cite{shirane}.
Experimental considerations
The 3 scattering angles, \(2\theta_{\rm m}\), \(2\theta\), and \(2\theta_{\rm a}\), are often denoted by the less-obvious symbols \(A2\), \(A4\), and \(A6\), respectively. The symbol \(A3\) denotes the sample rotation \(\omega_{\rm s}\), while the symbols \(A1\) and \(A5\) denotes the rotation of monochromator and analyzer crystals, respectively. This is also listed in table \ref{tab:As}.
Often, an experimental series consists of scans along a particular axis in \(({\bf q},\hbar\omega)\) space. One speaks about constant-energy scans and constant-q scans. For the latter, it is costumary to use a constant \(E_{\rm f}\) for the scans and then measure each scan point until a constant count number in the beam monitor has been reached. Since the sensitivity of the monitor is proportional to wavelength, \(\lambda_{\rm i}\), the number of neutrons reaching the sample for each scan point is proportional to \(1/\lambda_{\rm i}\) - or to \(k_{\rm i}\). These facts causes the factor \(k_{\rm f}/k_{\rm i}\) in the final cross section (\ref{eq:master_scatt_inel}) to be constant. Hence, the variation of this factor can be neglected, easing the subsequent data analysis.
Two types of spectrometers for a pulsed source
On instruments at pulsed sources, one can utilize time-of-flight techniques as for diffraction. However, the time-of-flight cannot be used to determine both \(E_{\rm i}\) and \(E_{\rm f}\). Either the initial or final energy must be selected by other means, typically by Bragg reflection from crystals or by chopping the beam in short time pulses close to the sample. This leads to two essentially different types of spectrometer geometries:
Direct geometry
The incoming neutrons are monochromatized by a chopper system and hits the sample in a short burst. Thus, \(E_{\rm i}\) is fixed, and the time-of-flight is used to determine the value of \(E_{\rm f}\).
Indirect geometry
The sample is hit by a "white" beam, and only outgoing neutrons with a particular energy are scattered by analyzer crystals on to the detector. Thus, \(E_{\rm f}\) is fixed and the time-of-flight is used to determine the value of \(E_{\rm i}\).
The advantages with time-of-flight spectroscopy are so large, that at many continuous sources one chooses to chop the beam close to the source, producing short pulses. In this way more than 99% of the neutrons coming through the guide system are sacrificed.
In later versions of these notes, there will be more material on time-of-flight spectrometers, including figures.
- ↑ J.A. Rodriguez et al. Macs - a new high intensity cold neutron spectrometer at nist. Meas. Sci Techn., 19:034023, 2006.
- ↑ K. Lefmann et al. Realizing the full potential of a rita spectrometer. Physica B, 385-386:1083-1085, 2006.
- ↑ M. Kempa et al. The flatcone multianalyzer setup for ill's three-axis spectrometers. Physica B, 385-386:1080, 2006.
