Scattering from lattice vibrations: Difference between revisions
ucph>Tommy No edit summary |
m (1 revision imported) |
(No difference)
| |
Latest revision as of 22:15, 18 February 2020
On the Diffraction from crystals page, we worked under the assumption that the nuclei of the crystalline material were fixed in position, when investigating diffraction from the lattice planes. This is, of course, not a realistic description. In this chapter, we will investigate how the motion of the nuclei can scatter neutrons inelastically. However, as we shall see, a large fraction of the scattering will still take place as diffraction, as described on the Diffraction from crystals page.
First, we will treat the physics of lattice vibrations in crystalline materials purely classically, later a quantum mechanical treatment is given, leading to quantized vibrations, or phonons. The latter is necessary for the detailed understanding of the inelastic neutron scattering cross section from crystals.
Along with the description of phonons, we will discover how lattice vibrations affect the intensity of the diffraction signals, leading to the Debye-Waller factor described on the Diffraction from crystals page.
Lattice vibrations, classical treatment
We will here describe lattice vibrations in general. This section deals with the purely classical description, while the section Phonons, quantum mechanical treatment introduces the quantum mechanical treatment.
Dynamical description of nuclei in crystals
Let us as before denote the equilibrium position of the nuclei with \({\bf r}_j\) -- or for a non-Bravais lattice \({\bf r}_j + \boldsymbol\Delta_i \) with \(j\) being the index for the unit cell and \(i\) labeling the atom within the unit cell. These atomic positions are constant in time (assuming that the crystal center-of-mass is at rest). We describe the motion of the nuclei with the (small) displacement vector \({\bf u}_{ij}(t)\). The time-dependent nuclear position now reads
\begin{equation}\label{eq:vibration} {\mathbf R}_{ij}(t) = {\mathbf r}_j + \boldsymbol\Delta_i + {\mathbf u}_{ij}(t) . \end{equation}
We approximate the potential energy between two neighbour atoms by a quadratic form in the difference between their displacements:
\begin{equation}\label{eq:harmonic_potential} V_{jj'} = \dfrac{1}{2} K_{jj'} ({\mathbf u}_{j}(t) - {\mathbf u}_{j'}(t))^2 + V_0, \end{equation}
where \(K_{jj'}\) is the spring constant for the (in this case isotropic) atom-atom interaction, \(V_0\) is a zero point of the energy, and we have dropped the subscripts \(i\) for convenience.
The one-dimensional nearest neighbour model
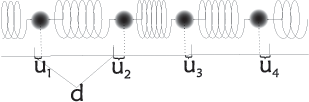
We will now turn to a few concrete one-dimensional examples, which will give much insight in the physics of phonons. We first consider a model of \(N\) identical particles (atoms) of mass \(M\), with equilibrium spacing \(a\), and identical nearest neighbour spring constants \(K\). This system is illustrated in Figure xx--CrossReference--fig:springs--xx. The equilibrium distance between atoms is \(a\), so we can write \(r_j = j a\).
The net spring force between two particles is zero in equilibrium (where all \(u_j=0\)). In the general case, the force on particle \(j\) from particle \(j+1\) reads:
\begin{equation} \label{dummy132847800} F_{j,j+1}(t) = K \left[ - u_j(t) + u_{j+1}(t) \right] , \end{equation}
where \(K\) is the spring constant of one spring. Including also the similar coupling \(F_{j-1,j}(t)\), the equation of motion for \(u_j\) can be written using Newton's second law:
\begin{equation}\label{eq:N2} M \dfrac{d^2}{dt^2} u_j(t) = K \left[ u_{j-1}(t) + u_{j+1}(t) - 2 u_j(t) \right] . \end{equation}
To simplify the calculations, we assume periodic boundary conditions, i.e. we assume that atom 1 is connected with atom \(N\) with a force term equivalent to \(F_{j,j+1}\). The error introduced by this so-called Born-von Karman boundary conditions will vanish in the thermodynamic limit (\(N \rightarrow \infty\)) and hence it is safe for us to make this choice that makes the problem mathematically simple. The periodic boundary conditions are equivalent to defining \(u_{N+1} \equiv u_1\).
We look for solutions to equation \eqref{eq:N2} of the plane wave form
\begin{equation}\label{eq:fourier} u_j(t) = A \exp(i q j a - i \omega_q t) , \, \end{equation}
where the real value of \(u_j(t)\) represent the physical displacement, while the imaginary part contains information on the phase of the vibrations. The amplitude for the vibrations, \(A\), is chosen to be real. The periodic boundary conditions imply that the phase is invariant under a translation of \(N\) atoms. This gives a choice of possible values of the wave vector:
\begin{equation} \label{dummy908100751} q = \dfrac{n}{N} a^* , \end{equation}
where \(n\) is an integer and the reciprocal lattice vector is \(a^* = 2\pi/a\).
Inserting equation \eqref{eq:fourier} into equation \eqref{eq:N2}, we reach
\begin{equation} \label{dummy475684766} -\omega_q^2 M u_j(t) = K u_j(t) \left[ \exp(iqa) + \exp(-iqa) - 2 \right]. \end{equation}
This simplifies directly into the dispersion relation we are looking for
\begin{equation}\label{eq:dispersion_1atom} \omega_q^2 = 2 \omega_0^2 \left[ 1- \cos(qa) \right] = 4 \omega_0^2 \sin^2(qa/2). \end{equation}
Here, the characteristic frequency, \(\omega_0\), is defined as the resonance frequency of the related single-particle harmonic oscillator,
\begin{equation}\label{eq:omega0} \omega_0 = \sqrt{\dfrac{K}{M}}. \end{equation}
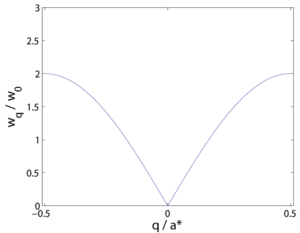
The dispersion relation for one Brillouin zone, \(| {\bf q} | \leq \pi/a = |{\bf a}^*| / 2\), is shown in Figure xx--CrossReference--fig:nn_dispersion--xx. At small \(q\), the dispersion is approximately linear, so it is meaningful to define a velocity of the lattice vibrations as
\begin{equation} \label{dummy1908810697} c = \dfrac{\partial \omega_q}{\partial q} \approx \omega_0 a . \end{equation}
These long-wavelength lattice vibrations are, in fact, the same as sound waves in materials. Therefore, this type of vibrations is known as acoustic.
As we shall see in the section Phonons, quantum mechanical treatment, the quantized lattice vibrations are known as phonons. The low-energy phonons are in analogy with the discussion above denoted acoustic phonons.
Optical lattice vibrations
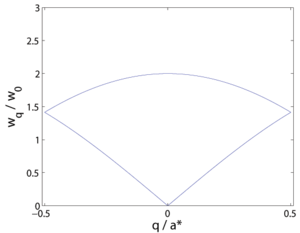
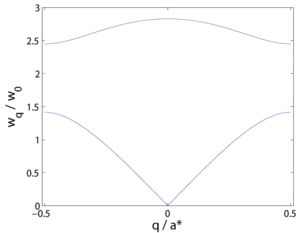
A symmetry breaking in the Bravais crystal can cause a doubling of the unit cell, even if it may have little effect on the vibration physics. This leads to reduction of the Brillouin zone by a factor 2, \(a_2^* = a^*/2\). The vibration modes are now denoted differently. The part of the dispersion relation that has the highest values of \(|q|\) is "folded back" by \(q_2 = q-a_2^*\) to create a second branch of the dispersion relation. This new, most often higher lying, branch is now denoted the optical branch. The optical and acoustic branches are shown in Figure xx--CrossReference--fig:nn_optical--xx.
The optical mode for \(q=0\) is particularly easy to interpret: All unit cells behave identically, while the two atoms in the unit cell vibrate in counter phase. In the original system, Figure xx--CrossReference--fig:nn_dispersion--xx, this corresponds to the zone boundary: \(q = \pi/a\). The frequency at this position is \(\omega_{\pi/a} = 2 \omega_0\).
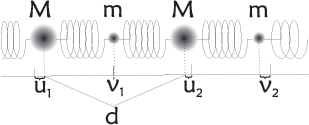
For the sake of self-consistency, let us calculate the above result explicitly. To describe this motion quantitatively, we denote the displacement of the first atom in the \(j\)'th unit cell \(u_j(t)\), while the second atom is denoted \(v_j(t)\). The equation of motion now reads
\begin{align} \label{eq:general2} M \dfrac{d^2}{dt^2} u_j(t) &= K \left[ v_{j-1}(t) + v_j(t) - 2 u_j(t) \right] , \\ M \dfrac{d^2}{dt^2} v_j(t) &= K \left[ u_{j+1}(t) + u_j(t) - 2 v_j(t) \right] .\nonumber \end{align}
Since \(q=0\), the motion is independent of \(j\). Hence, we can reduce the expression to:
\begin{align} \label{eq:optical1} \omega^2 u(t) &= 2 \omega_0^2 \left[ u(t) - v(t) \right] , \\ \omega^2 v(t) &= 2 \omega_0^2 \left[ v(t) - u(t) \right] .\nonumber \end{align}
This is the same equation of motion as for two identical particles connected by one spring with strength \(2K\). When we take into account that the two atoms in the unit cell move in counter phase, we have \(u(t) = - v(t)\), leading to \(\omega = 2 \omega_0\), as we aimed to show.
In general, for a one-dimensional system with \(N\) atoms in the unit cell, there will be 1 acoustic and \(N-1\) optical modes.
One-dimensional models with two different atoms
Let us now treat the one-dimensional system with identical springs of constant \(K\), but two different atoms per unit cell. This is illustrated in Figure xx--CrossReference--fig:springs2--xx.
The masses of the two atoms are denoted \(m\) and \(M\), respectively, with \(M\) the largest of the two. We define
\begin{equation}\label{eq:twoatoms} \beta = \frac{m}{M} < 1 , \end{equation}
and \(\omega_0\) is defined as in equation \eqref{eq:omega0}.
Solving the equations of motion for the two atoms (see Problem: Classical vibrations with a two-atom unit cell), we reach the dispersion relation
\begin{equation}\label{eq:spring2d} \omega_q^2 = 2 \omega_0^2 \left[1-\cos(qa/2) \alpha^{-1} \right] , \end{equation}
where \(\alpha\) is the ratio of vibration amplitudes for the two types of atoms:
\begin{equation} \label{dummy2033491713} \alpha = \dfrac{1-\beta \pm \sqrt{(1-\beta)^2 + 4 \beta\cos^2(qa/2)}}{2\cos(qa/2)} . \end{equation}
Note that for \(q \rightarrow 0\), we have the solutions \(\alpha_1 = 1\) (long-wave acoustic phonons) and \(\alpha_2 = -\beta\); the \(q=0\) optical phonons, where the atoms move in counter phase and the light atoms vibrate with a larger amplitude. The resulting dispersion relation for \(\beta=1/3\) is shown in Figure xx--CrossReference--fig:2atom_dispersion--xx.
*Phonons in three dimensions
The problems has been treated in a number of textbooks, e.g. in Squires, Appendix G[2]. The solution is very similar to the one-dimensional case, except that the phonons now have both a (three-dimensional) \({\bf q}\) and a polarization vector, \({\bf e}_{q,p}\), which represents the direction of the vibration:
\begin{equation} \label{dummy1137015881} {\mathbf u}_j(t) = \sqrt{\dfrac{\hbar}{2 M N}} \displaystyle\sum_{q,p} \dfrac{{\mathbf e}_{q,p}}{\sqrt{\omega_{q,p}}} \left[ a_{q,p} \exp(i({\mathbf q}\cdot {\mathbf r}_j - \omega_{q,p} t)) + a^\dagger_{q,p} \exp(-i({\mathbf q}\cdot {\mathbf r}_j - \omega_{q,p} t)) \right] , \end{equation}
where \(p\) is the polarization index, which runs over 3 times the number of atoms in the unit cell. The Hamiltonian for the phonon system reads
\begin{equation} \label{dummy1572956896} H = \displaystyle\sum_{q,p} \hbar \omega_{q,p} \left( a^\dagger_{q,p} a_{q,p} + \dfrac{1}{2} \right) . \end{equation}
In general, there are two types of phonons:
- Longitudinal: The polarization vector \({\bf e}_{q,p}\) is parallel to \({\bf q}\).
- Transverse: The two polarization vectors \({\bf e}_{q,p}\) are perpendicular to \({\bf q}\). Usually, these modes have lower energies than the longitudinal ones.
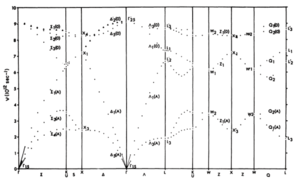
For a non-Bravais lattice with \(m\) atoms per unit cell, there are only 3 acoustic modes. The remaining \(3(m-1)\) are optical modes with a non-zero frequency (often a local maximum) at \(q=0\). A typical set of phonon dispersion curves for a two-atom unit cell (Ge) is presented in Figure xx--CrossReference--fig:phonon--xx.
The role of lattice vibrations in materials
The lattice vibrations determine a number of properties of materials. A straigtforward example is the acoustic properties, where the acoustic phonons are equal to sound waves.
An important consequence of lattice vibrations is the thermodynamic properties of materials. In fact the heat capacity and thermal conductivity in insulating materials stem from the lattice vibrations.
As we shall see in the Phonons, quantum mechanical treatment section, the lattice vibrations quantize in energy units of \(\hbar \omega_q\). These quasiparticles are denoted phonons and are approximately Bosons, i.e. there can be several phonons with the same \({\bf q}\); a larger number of phonons corresponds to larger classical vibration amplitudes. The occupation numbers of phonons are thus given by Bose-Einstein statistics,
\begin{equation} n_{q} = n_{\rm B}(\hbar \omega_q/k_{\rm B}T) . \end{equation}
where \(n_{\rm B}\) is the Bose occupation number
\begin{equation} \label{eq:nB} n_{\rm B}\left(\frac{\hbar\omega}{k_{\rm B}T}\right) = \frac{1}{\exp\left( \dfrac{\hbar\omega}{k_{\rm B}T} \right) - 1} \, . \end{equation}
These equations form, together with knowledge of the dispersion relation, \(\omega_q\), the basis for the description of the thermal properties of phonons, which is elaborated on in many textbooks, e.g. the one by Kittel[1]. Is it therefore essential to measure the phonon dispersion relations in order to understand thermal properties of materials.
Another, and more complex part of phonon science is the study of crystal anharmonicities, caused by 4'th and higher order terms in the atomic potentials. Anharmonicities give rise to e.g. thermal expansion, and can be inferred from studies of phonon lifetimes, which in turn can be found by studying the energy spread in the phonon energies. This is, however, beyond the scope of these notes.
- ↑ C. Kittel. Introduction to Solid State Physics. Wiley, 2004.
*Phonons, quantum mechanical treatment
With the discussion on lattice vibrations (last section) in mind, we now treat the problem of lattice vibrations quantum mechanically. We will show how the vibrations with frequencies \(\omega_q\) of the classical solution quantize into bosonic phonons, which has wavenumber \({\bf q}\) and energy \(\hbar \omega_q\).
*The harmonic oscillator
The solution to the phonon problem lends much from the standard example of one particle in a harmonic potential. Therefore, it is of value to summarize this solution here. A more thorough derivation is given in most textbooks on quantum mechanics.
We consider a particle of mass \(M\) in a one-dimensional periodic potential. The Hamiltonian is given as
\begin{equation}\label{eq:HOhamil} H = \dfrac{p^2}{2M} + \dfrac{K x^2}{2} , \end{equation}
where \(p\) is the momentum operator, \(p = i \hbar \partial/\partial x\), and \([x,p]=i\hbar\). We recall that the classical oscillator frequency is given by equation \eqref{eq:omega0} and define the creation and annihilation operators as
\begin{align} a^\dagger &= \dfrac{1}{\sqrt{2\hbar\omega_0 M}} \left( M \omega_0 x + i p \right) . \label{dummy915753937}\\ a &= \dfrac{1}{\sqrt{2\hbar\omega_0 M}} \left( M \omega_0 x - i p \right) .\label{dummy1648971532} \end{align}
These operators are normalized so that
\begin{equation} \label{dummy1883154453} [a,a^\dagger] = 1 . \end{equation}
This commutation relation show that \(a\) and \(a^\dagger\) are boson operators. We can obtain the position and momentum operators:
\begin{align} x &= \sqrt{\dfrac{\hbar}{2\omega_0 M}} \left(a^\dagger + a\right) . \label{dummy1083051975}\\ p &= -i \sqrt{\dfrac{\hbar\omega_0 M}{2}} \left(a^\dagger - a\right) .\label{dummy102554818} \end{align}
By substitution into equation \eqref{eq:HOhamil}, we reach
\begin{equation} \label{dummy2070323948} H = \hbar \omega_0 \left( a^\dagger a + \frac{1}{2}\right) , \end{equation}
where \(a^\dagger a\) is the number operator, \(n\), with eigenvalues being integers from zero and upwards. The oscillation is thus quantized with energy quanta of \(\hbar\omega_0\). Notice that even the ground state has a finite energy, \(E_{\rm gs} = \hbar \omega_0 / 2\). This is called the zero point energy. The zero point energy is related to a "smearing" of the ground state, due to Heisenberg's uncertainty principle, which in this case is denoted zero point motion.
*The one-dimensional quantum model
This lattice model is solved in much the same way as for the one-particle harmonic oscillator. We can write the Hamiltonian as the sum of the kinetic energy and a harmonic potential of the form in equation \eqref{eq:harmonic_potential}:
\begin{equation}\label{eq:H_1d_phonon} H = \displaystyle\sum_j \left[ \dfrac{p_j^2}{2M} + \dfrac{K}{2} \left(u_j-u_{j+1} \right)^2 \right] . \end{equation}
We now perform a Fourier transform of the displacement operators:
\begin{align} u_q &= \dfrac{1}{\sqrt{N}} \displaystyle\sum_j \exp(i q j a) u_j , \label{dummy801882678}\\ u_j &= \dfrac{1}{\sqrt{N}} \displaystyle\sum_q \exp(- i q j a) u_q ,\label{dummy1978718886} \end{align}
and similar for the \(p_j\) operators. We have here applied periodic Born-von Karman boundary conditions as in the classical case: \(u_{N+1} \equiv u_1\), and used that the equilibrium positions are given by \(r_j = j a\). Inserting this into equation \eqref{eq:H_1d_phonon}, we reach
\begin{equation}\label{eq:H_1d_phonon2} H = \displaystyle\sum_{jqq'} \exp\big(-i(q+q')ja \big) \biggr[ \dfrac{p_q p_{q'}}{2MN} + \dfrac{K}{2N}\left(u_q u_{q'}\{1-\exp(-iqa)\}\{1-\exp(-iq'a)\}\right)\biggr]. \end{equation}
The sum over \(j\) depends only on the first exponential function. This is summed out to give \(N \delta_{q,-q'}\). Next, the sum over \(q'\) is easily performed yielding
\begin{align} \label{eq:H_1d_phonon3} H &= \displaystyle\sum_{q} \left[ \dfrac{p_q p_{-q}}{2M} + K \left(u_q u_{-q}\{1-\cos(qa)\}\right)\right] \\ &= \displaystyle\sum_{q} \left[ \dfrac{p_q p_{-q}}{2M} + \dfrac{M}{2} \left(u_q u_{-q}\omega_q^2 \right)\right], \nonumber \end{align}
where we in the last step have used the expression for the classical vibration frequency, \(\omega_q\), from equation \ref{eq:dispersion_1atom}.
We now define the Fourier transformed creation and annihilation operators as
\begin{align} a_q^\dagger &= \dfrac{1}{\sqrt{2\hbar\omega_q M}} \left( M \omega_q u_q + i p_q \right) . \label{dummy1154685165}\\ a_q &= \dfrac{1}{\sqrt{2\hbar\omega_q M}} \left( M \omega_q u_q - i p_q \right) .\label{dummy32026784} \end{align}
It can be shown that these operators describe bosons, through
\begin{equation} \label{dummy1259932973} [a_q,a_q^\dagger] = 1 . \end{equation}
The operators \(u_q\) and \(p_q\) are given by:
\begin{align} u_q &= \sqrt{\dfrac{\hbar}{2\omega_q M}} \left(a_q^\dagger + a_q\right) . \label{dummy964522178}\\ p_q &= -i \sqrt{\dfrac{\hbar\omega_q M}{2}} \left(a_q^\dagger - a_q\right) .\label{dummy187797063} \end{align}
Inserting into the Hamiltonian in equation \ref{eq:H_1d_phonon3}, we reach the final solution
\begin{equation} \label{dummy1773738828} H = \displaystyle\sum_q \left(a_q^\dagger a_q + \dfrac{1}{2}\right) \hbar \omega_q . \end{equation}
This shows that the system is described by \(N\) independent oscillator modes (phonons), distinguished by their wave number \(q\).
*Quantum mechanical formalism in three dimensions
The general features of three-dimensional phonons is described in Lattice vibrations, classical treatment.
To make a quantum mechanical descriptiopn, one needs the displacement operators to include the polarization vector, \({\bf e}_{q,p}\):
\begin{equation} {\bf u}_j(t) = \sqrt{\frac{\hbar}{2 M N}} \sum_{q,p} \frac{{\bf e}_{q,p}}{\sqrt{\omega_{q,p}}} \times \left[ a_{q,p} \exp(i({\bf q}\cdot {\bf r}_j - \omega_{q,p} t)) + a^\dagger_{q,p} \exp(-i({\bf q}\cdot {\bf r}_j - \omega_{q,p} t)) \right] , \end{equation}
where \(p\) is the polarization index, which runs over 3 times the number of atoms in the unit cell.
In this version of the notes, we make no attempt of solving this problem. In stead, we just show the final result for the phonon Hamiltonian: \begin{equation} H = \sum_{q,p} \hbar \omega_{q,p} \left( a^\dagger_{q,p} a_{q,p} + \frac{1}{2} \right) . \end{equation} This shows that also in three dimensions the lattice vibrations are quantized in terms of Bosonic phonons, with energies depending upon both \({\bf q}\) and \(p\).
*The scattering cross section for phonons
We will now proceed to calculate the inelastic scattering cross section for phonons in a crystal. As a first attempt, and to build intuition, we use a classical interpretation of equation (\ref{eq:sum_lambda_f}) for general inelastic nuclear scattering equation.
Inelastic cross section of atoms in a lattice
As a start, we make the assumption that the nuclei vibrate around their equilibrium positions, eq. (\ref{eq:vibration}). The cross section then becomes \begin{align}\label{eq:vibration} \frac{d^2\sigma}{d\Omega dE_{\rm f}} &= \frac{k_{\rm f}}{k_{\rm i}} \sum_{j,j'} \frac{b_j b_{j'}}{2 \pi \hbar} \exp(i {\bf q} \cdot (-{\bf r}_j+{\bf r}_{j'})) \\ &\quad \times \int_{-\infty}^{\infty} \big\langle \exp(-i {\bf q} \cdot {\bf u}_j(0)) \exp(i {\bf q} \cdot {\bf u}_{j'}(t)) \big\rangle \exp(-i\omega t) dt \nonumber . %} \, . \end{align}
We next make the assumption that the atoms are placed in a crystal, {\i.e.} with translational symmetry (as for crystal diffraction). Then, we replace the sum over \(j\) and \(j'\) with \(N\) times the sum over \(j\), and \(-{\bf r}_j+{\bf r}_{j'}\) by \({\bf r}_j\). For reasons of simplicity, we assume a Bravais lattice \begin{align} \left.\frac{d^2\sigma}{d\Omega dE_{\rm f}}\right|_{\rm Bravais} &= \frac{k_{\rm f}}{k_{\rm i}} \frac{N b^2}{2 \pi \hbar} \sum_{j} \exp(i {\bf q} \cdot {\bf r}_j) \\ &\quad \times \int_{-\infty}^{\infty} \big\langle \exp(-i {\bf q} \cdot {\bf u}_0(0)) \exp(i {\bf q} \cdot {\bf u}_{j}(t)) \big\rangle \exp(-i\omega t) dt \nonumber . %} \, . \end{align} We now utilize that the displacement from equilibrium, \(u_j(t)\), is small, so that we can Taylor expand the exponential functions. We also utilize that \(\langle u_j(t) \rangle = 0\), so that only even powers of \(u_j(t)\) contribute, reaching: \begin{equation} \big\langle \exp(-i {\bf q} \cdot {\bf u}_0(0)) \exp(i {\bf q} \cdot {\bf u}_{j}(t)) \big\rangle \approx \langle 1 - ({\bf q} \cdot u_0(0))^2/2 - ({\bf q} \cdot u_j(t))^2/2 + ({\bf q} \cdot u_0(0))({\bf q} \cdot u_j(t)) \rangle . \end{equation} The factor 1 and the square terms above each have a constant time average and therefore leads to diffraction. In fact, they becomes the Debye-Waller factor, already discussed under diffraction. %ToDo: develop this better We here concentrate on the mixed term leading to phonon cross section: \begin{align} \label{eq:phonon_cross_classical_3} \left.\frac{d^2\sigma}{d\Omega dE_{\rm f}}\right|_{\rm Bravais, 1~ph.} &= \frac{k_{\rm f}}{k_{\rm i}} \frac{N b^2}{2 \pi \hbar} \sum_{j,j'} \exp(i {\bf q} \cdot {\bf r}_j) \\ &\quad \times \int_{-\infty}^{\infty} \big\langle ({\bf q} \cdot {\bf u}_0(0)) ({\bf q} \cdot {\bf u}_{j}(t)) \big\rangle \exp(-i\omega t) dt \nonumber . %} \, . \end{align} To calculate the cross section, we need to know the vibration function, \({\bf u}_j(t)\). However, since this is a linear problem, it is sufficient to calculate for one vibration (or phonon) frequency, and then add the results in the end. We thus assume the vibrations to be described by (in one dimension for simplicity) \begin{equation} \label{eq:vibration_phase} {\bf u}_j(t) = A_q \left( \exp(i q j a - i \omega_q t + i \phi) + {\rm complex\, conjugate}\right) , \end{equation} where \(\phi\) is a phase factor. It is important here to remember that \({\bf u}_j(t)\) is always a real number, even though it is convenient to describe it with complex exponentials.
Inserting (\ref{eq:vibration_phase}) into (\ref{eq:phonon_cross_classical_3}), we reach terms of the form \begin{equation} \big\langle (\exp(i \phi) + \exp(-i \phi)) (\exp(i q j a) \exp(-i \omega_q t) \exp(i \phi) + \exp(-i q j a) \exp(i \omega_q t) \exp(-i \phi)) \big\rangle . \end{equation} The thermal average is in effect equivalent to averaging over the phase factor, as well as replacing \(A_q\) with \(\langle A_q \rangle\). The above equation then simplifies to \begin{equation} (\exp(i q j a) \exp(-i \omega_q t) + \exp(-i q j a) \exp(i \omega_q t) ) . \end{equation} Inserting into (\ref{eq:phonon_cross_classical_3}), we reach \begin{align} \label{eq:phonon_cross_classical_4} \left.\frac{d^2\sigma}{d\Omega dE_{\rm f}}\right|_{\rm Bravais, 1~ph.} &= \frac{k_{\rm f}}{k_{\rm i}} \frac{N b^2 \langle A_q^2 \rangle ({\bf q} \cdot \hat{e}_p)^2}{2 \pi \hbar} \sum_{j} \exp(i {\bf q} \cdot {\bf r}_j) \\ &\quad \times \int_{-\infty}^{\infty} (\exp(i q j a) \exp(-i \omega_q t) + \exp(-i q j a) \exp(i \omega_q t) ) \exp(-i\omega t) dt \nonumber , %} \, . \end{align} for which the Fourier transforms over space and time are performed to give \begin{align} \label{eq:phonon_cross_classical_5} \left.\frac{d^2\sigma}{d\Omega dE_{\rm f}}\right|_{\rm Bravais, 1~ph.} &= \frac{k_{\rm f}}{k_{\rm i}} N \frac{(2 \pi)^3}{V_0}\langle A_q^2 \rangle b^2 ({\bf q} \cdot \hat{e})^2 \sum_{bf \tau} \\ &\quad \times \left[ \delta(\omega-\omega_{q}) \delta({\bf q}-{\bf q}'+{bf \tau}) + \delta(\omega+\omega_{q}) \delta({\bf q}+{\bf q}'+{bf \tau}) \right] \nonumber , %} \, . \end{align} where \(\hat{e}\) is a unit vector in the direction of the vibration.
The full quantum mechanical description, given in section \ref{sect:phonon_quantic}, essentially agrees with the classical calculation above. Here, the mean squared vibration amplitude, \(\langle A_q^2 \rangle\), is found to be related to the thermal Bose factor, \(n_q\). In addition, quantum effects produce a difference between the prefactors of the two sets of delta functions. The final cross section reads
\begin{align} \label{eq:cross_one_phonon} \left.\frac{d^2\sigma}{d\Omega dE_{\rm f}}\right|_{\rm Bravais, 1~ph.} &= \frac{k_{\rm f}}{k_{\rm i}} \frac{b^2(2\pi)^3}{2 M V_0} \exp(-2W) \sum_{q,p,\tau} \frac{({\bf q}\cdot {\bf e}_{q,p})^2}{\omega_{q,p}} \\ &\quad\times \left[ (n_{q,p}+1) \delta(\omega-\omega_{q,p}) \delta({\bf q}-{\bf q}'+{bf \tau}) \right. \nonumber \\ &\qquad \left. + n_{q,p} \delta(\omega+\omega_{q,p}) \delta({\bf q}+{\bf q}'+{bf \tau}) \right] , \nonumber \end{align} where a polarization index, \(p\), has been added to the phonon modes.
Understanding the one-phonon cross section
We now like to discuss the interpretation of the phonon cross section (\ref{eq:cross_one_phonon}), starting with the last two lines. In the first term in the square brackets, the neutron looses energy, while the lattice gains the same amount, \(\hbar\omega_{q,p}\). Hence, this corresponds to the creation of one phonon. Likewise, in the second term the neutron gains energy, while the lattice loses, representing annihilation of one phonon. The population factors, \(n_{q,p}\) and \(n_{q,p}+1\) give the physically meaningful result that at zero temperature (\(n_{q,p}=0\)), phonon annihilation has zero cross section (no phonons are present), while phonon creation is still allowed.
The term \(({\bf q}\cdot {\bf e}_{q,p})^2\) in (\ref{eq:cross_one_phonon}) implies that the neutron only senses vibrations {\em parallel} to the total scattering vector. This intuitively makes sense, since a displacement of the nucleus perpendicular to {\bf q} would not change the phase of the scattering.
Experimental considerations
The dependence of the scattering cross section on \(({\bf q}\cdot {\bf e}_{q,p})^2\) has strong implications on the experimental strategy. If, {\em e.g.}, in a cubic system you like to study longitudinal phonons, you first like to find the highest reasonable value of \(q\), for example \((0\, 0\, 6)\). Next, you like to investigate the scattering along \((0\, 0\, 6+l)\) to pick up the longitudinal vibrations. In contrast, for transverse phonons, you should look along another direction, for example \((h\, 0\, 6)\), since these phonons have polarization transverse to the \((h\, 0\, 0)\) direction, not to \({\bf q}\).
If one wants to study all vibration directions in a crystal of low symmetry, it may be necessary to investigate the phonon spectrum in different Brillouin zones to change the angle between the scattering vector, \({\bf q}\), and the phonon wave vector, \({\bf q}'\).
*Quantum mechanical derivation of neutron-phonon scattering
We will now make a quantum mechanical derivation of the inelastic scattering cross section (\ref{eq:sum_lambda_f}) for the case of phonons in a crystal. Along the way, we touch upon a proper derivation of the Debye-Waller factor from the description of neutron diffraction (\ref{eq:diffraction_DW}).
* Inelastic cross section of atoms in a lattice
We make the usual assumption that the nuclei vibrate around their equilibrium positions, eq.~(\ref{eq:vibration}), and we use the translational symmetry of the crystal, so that (as for crystal diffraction) the sum over \(j\) and \(j'\) equals \(N\) times the sum over \(j\):
\begin{align} &\sum_{j,j',i,i'} b_{j,i} b_{j',i'} \big\langle \exp(-i {\bf q} \cdot {\bf R}_{j,i}(0)) \exp(i {\bf q} \cdot {\bf R}_{j',i'}(t)) \big\rangle \\ \nonumber &\quad= N \sum_{i,i'} b_i b_{i'} \exp(i {\bf q} \cdot ({\bf \Delta}_{i'}-{\bf \Delta}_i)) , \sum_{j'} \exp(i {\bf q} \cdot {\bf r}_{j'}) \\ &\quad\quad \times \big\langle \exp(-i {\bf q} \cdot {\bf u}_{0,i}(0)) \exp(i {\bf q} \cdot {\bf u}_{j',i'}(t)) \big\rangle \nonumber \\ &\quad= N |F_{\rm N}({\bf q})|^2 \sum_{j',i,i'} \exp(i {\bf q} \cdot {\bf r}_{j'}) \big\langle \exp(-i {\bf q} \cdot {\bf u}_{0,i}(0)) \exp(i {\bf q} \cdot {\bf u}_{j',i'}(t)) \big\rangle \nonumber \end{align}
where we recognize the nuclear structure factor, \(F_{\rm N}({\bf q})\), from (\ref{eq:structurefactor}). The scattering cross section now becomes \begin{align} \frac{d^2\sigma}{d\Omega dE_{\rm f}} &= \frac{k_{\rm f}}{k_{\rm i}} \frac{N |F_{\rm N}({\bf q})|^2}{2 \pi \hbar} \sum_{j,i,i'} \exp(i {\bf q} \cdot {\bf r}_j) \\ &\quad\times \int_{-\infty}^{\infty} \big\langle \exp(-i {\bf q} \cdot {\bf u}_{0,i}(0)) \exp(i {\bf q} \cdot {\bf u}_{j,i'}(t)) \big\rangle \, \exp(-i \omega t) dt \nonumber . \end{align}
For a Bravais lattice (one atom per unit cell), the sum over the \(i\)'s disappear, and \(F_{\rm N}({\bf q}) = b\). Here, we can specialize the cross section to yield
\begin{align} \label{eq:cross_phonon_1} \left. \frac{d^2\sigma}{d\Omega dE_{\rm f}}\right|_{\rm Bravais} &= \frac{k_{\rm f}}{k_{\rm i}} \frac{Nb^2}{2 \pi \hbar} \sum_{j} \exp(i {\bf q} \cdot {\bf r}_j) \\ &\quad \times \int_{-\infty}^{\infty} \big\langle \exp(-i {\bf q} \cdot {\bf u}_0(0)) \exp(i {\bf q} \cdot {\bf u}_{j}(t)) \big\rangle \exp(-i\omega t) dt . \nonumber \end{align}
Details of phonon operators
The difficult portion of the phonon cross section (\ref{eq:cross_phonon_1}) is now the operator exponential functions, which are of the type \(\langle \exp(U) \exp(V) \rangle\).
A quantum mechanical theorem [1] states that if \([U,V]\) is a c-number (in contract to being another operator), then \begin{equation} \langle \exp(U) \exp(V) \rangle = \langle \exp(U+V) \rangle \exp\left(\frac{1}{2}[U,V]\right) . \end{equation}
Let us take a closer look at \(U\) and \(V\). Both can be put in the form: \begin{align} U &= -i {\bf q} \cdot {\bf u}_0(0) = -i \sum_{q,p} (g_{q,p} a_{q,p} + g^*_{q,p} a_{q,p}^\dagger) , \\ V &= i {\bf q} \cdot {\bf u}_j(t) = i \sum_{q,p} (h_{q,p} a_{q,p} + h_{q,p}^* a_{q,p}^\dagger) , \end{align} where the coefficients are given by \begin{align} g_{q,p} &= \sqrt{\frac{\hbar}{2MN}} \frac{{\bf q} \cdot {\bf e}_{q,p}}{\sqrt{\omega_{q,p}}} . \\ h_{q,p} &= \sqrt{\frac{\hbar}{2MN}} \frac{{\bf q} \cdot {\bf e}_{q,p}}{\sqrt{\omega_{q,p}}} \exp(i {\bf q} \cdot {\bf r}_j) \exp(-i \omega_{q,p}t) . \end{align} Now, we calculate \([U,V]\), which becomes a quadruple sum. To ease our task, we note that \([a_{q,p},a^\dagger_{q',p'}]\) is nonzero only if \(q=q'\) and \(p=p'\). We can now show that \([U,V]\) is a c-number and calculate its value: \begin{align} [U,V] &= \sum_{q,p,q',p'} [g_{q,p} a_{q,p} + g_{q,p} a_{q,p}^\dagger, h_{q',p'} a_{q',p'} + h_{q',p'}^* a_{q',p'}^\dagger] \nonumber \\ &= \sum_{q,p} g_{q,p}h_{q,p}^* [a_{q,p},a^\dagger_{q,p}] + g_{q,p}h_{q,p} [a^\dagger_{q,p},a_{q,p}] \nonumber \\ &= \sum_{q,p} (g_{q,p}h_{q,p}^* - g_{q,p}h_{q,p}). \end{align}
Another theorem proves that for any harmonic oscillator operator (e.g. \(U\) or \(V\)): \begin{equation} \left\langle \exp(U) \right\rangle = \exp\left(\frac{1}{2}\left\langle U^2 \right\rangle\right) . \end{equation}
We now use this theorem to reach \begin{align} \left\langle \exp(U+V) \right\rangle \exp(\frac{1}{2}[U,V]) &= \exp\left(\frac{1}{2}\left\langle U^2+V^2+UV+VU+UV-VU \right\rangle\right) \nonumber \\ &= \exp(\langle U^2 \rangle) \exp(\langle UV \rangle) . \end{align} In the last step, we have used that \(\langle U^2 \rangle = \langle V^2 \rangle\). This can be argued by noting that the only differences between these harmonic operators are their time and position. Since the system is translation- and time invariant, the two expectations values must be identical.
* The phonon expansion
We first summarize the expression for the (Bravais lattice) phonon cross section so far: \begin{align} \label{eq:cross_phonon_2} \left.\frac{d^2\sigma}{d\Omega dE_{\rm f}}\right|_{\rm Bravais} &= \frac{k_{\rm f}}{k_{\rm i}} \frac{Nb^2}{2 \pi \hbar} \exp(\left\langle U^2 \right\rangle) \\ &\quad\times \sum_{j} \exp(i {\bf q} \cdot {\bf r}_j) \int_{-\infty}^{\infty} \exp(\left\langle UV \right\rangle) \exp(-i\omega t) dt . \nonumber \end{align} The most significant part of this expression is the operator \(\exp(\langle UV \rangle)\), which can create or annihilate a number of phonons. We proceed by a series expansion of the exponential:
\begin{equation} \label{eq:UVexpansion} \exp(\langle UV \rangle) \approx 1 + \langle UV \rangle + \frac{1}{2} \langle (UV)^2 \rangle + \,\cdots \end{equation} The zero'th order term we have dealt with before. Here, the time integral in (\ref{eq:cross_phonon_2}) results in \(2\pi\hbar \delta(\hbar\omega)\), i.e. elastic scattering. The cross section resulting from this term essentially equals (\ref{eq:diffract2}), which for crystalline materials leads to the Bragg law, modified by \(\exp(\left\langle U^2 \right\rangle) \), which is the Debye-Waller factor, to be elaborated in section~\ref{subsect:DW}.
The first order term \(UV\) in (\ref{eq:UVexpansion}) corresponds to creation or annihilation of one single phonon. This will be discussed in section \ref{sect:cross_single_phonon}. Likewise, the term \((UV)^2\) describes processes involving two phonons, and so on. We will here discuss only one-phonon processes. The multi-phonon processes will lead to a continuum of scattering, difficult to detect and analyze. This is to some extent discussed in Squires [1].
* The Debye-Waller factor
We now look closer at the term \(\langle U^2 \rangle\). Using the definition of \(U\), we can write \begin{align} \langle U^2 \rangle &= - \sum_i p_i \left\langle \lambda_i \left| U^2 \right| \lambda_i \right\rangle \nonumber \\ &= - \sum_i p_i \biggr\langle \lambda_i \biggr| \sum_{q,p,q',p'} g_{q,p} g_{q',p'} (a_{q,p}+a^\dagger_{q,p})(a_{q',p'}+a^\dagger_{q',p'}) \biggr| \lambda_i \biggr\rangle \nonumber \\ &= - \sum_{q,p} g_{q,p}^2 \sum_i p_i \left\langle \lambda_i \left| a_{q,p}a^\dagger_{q,p}+a^\dagger_{q,p}a_{q,p} \right| \lambda_i \right\rangle \nonumber \\ &= - \sum_{q,p} g_{q,p}^2 \left( 2 n_{\rm B}\left( \frac{\hbar \omega_{q,p}}{k_{\rm B}T} \right) + 1 \right) \nonumber \\ &= - \frac{\hbar}{2 M N} \sum_{q,p} \frac{\left( {\bf q} \cdot {\bf e}_{q,p}\right)^2}{\omega_{q,p}} \left( 2 n_{\rm B}\left( \frac{\hbar\omega_{q,p}}{k_{\rm B}T} \right) + 1 \right) , \end{align} where the expectation value \(\left\langle a_{q,p}^\dagger a_{q,p} \right\rangle\) has been replaced by its value \(n_{\rm B}\), the Bose occupation number (\ref{eq:nB}). In the derivation, we have also used that the expectation value is non-zero only when the number of \(a\) and \(a^\dagger\) operators is the same for each \((q,p)\). For example, the expression \(a_{q,p}^\dagger a_{q',p'}^\dagger |\lambda\rangle\) gives you the state \(|\lambda\rangle\) with two additional phonons, whence \(\langle\lambda|a_{q,p}^\dagger a_{q',p'}^\dagger | \lambda\rangle = 0\).
It is customary to define \(2W = -\langle U^2 \rangle\) and then define the Debye-Waller factor \begin{equation} \exp(-2W) \equiv \exp(\langle U^2 \rangle) \, . \end{equation} This is used to describe the reduction in diffraction intensity due to lattice vibrations, as was anticipated in chapter~\ref{ch:powder}. For a cubic crystal it can be shown that
\begin{equation} 2W = \frac{1}{3} q^2 \langle u^2 \rangle , \end{equation} where \(u\) is the mean atomic displacement from equilibrium. Using this as representative for all crystals, we can see that \(2W\) is non-zero at zero temperature (due to zero-point motion) and increases with temperature. As a consequence, the resulting Debye-Waller factor is slightly below unity at low temperatures, decreasing at higher temperatures.
Since \(2W\) is proportional to \(q^2\), the Debye-Waller factor can be approximated by unity in small-angle scattering; as we did implicitly in Small angle neutron scattering, SANS.
* The final scattering cross section for phonons
Using (\ref{eq:cross_phonon_2}) as a starting point, we continue to develop the operator values.
\begin{align} \langle UV \rangle &= \sum_i p_i \left\langle \lambda_i \left| UV \right| \lambda_i \right\rangle \nonumber \\ &= \sum_i p_i \biggr\langle \lambda_i \biggr| \sum_{q,p} \left(g_{q,p}a_{q,p}+g_{q,p}a^\dagger_{q,p}\right) \left(h_{q,p}a_{q,p}+h^*_{q,p}a^\dagger_{q,p}\right) \biggr| \lambda_i \biggr\rangle \nonumber \\ &= \sum_{q,p} \sum_i p_i \left\langle \lambda_i \left| \left(g_{q,p}a_{q,p}h^*_{q,p}a^\dagger_{q,p} +g_{q,p}a^\dagger_{q,p}h_{q,p}a_{q,p}\right) \right| \lambda_i \right\rangle \nonumber \\ &= \sum_{q,p} g_{q,p}h^*_{q,p} (n_{q,p}+1) + g_{q,p}h_{q,p}n_{q,p} , \end{align} where we have used that the expectation values for a pair of creation-annihilation operators is non-zero only if they have the same quantum numbers. Using the expression for the \(g\)'s and \(h\)'s, we reach \begin{align} \langle UV \rangle &= \frac{\hbar}{2MN} \sum_{q,p} \frac{({\bf q}\cdot {\bf e}_{q,p})^2}{\omega_{q,p}} \\ &\quad \times \big( \exp(-i {\bf q} \cdot {\bf r}_j+i \omega_{q,p}t) (n_{q,p}+1) + \exp(i {\bf q} \cdot {\bf r}_j-i \omega_{q,p}t) n_{q,p} \big) . \nonumber \end{align} We now insert this into (\ref{eq:cross_phonon_2}). To avoid confusion of labels, we use \({\bf q}'\) for the phonon wave vector. \begin{align} \label{eq:cross_phonon_3} \frac{d^2\sigma}{d\Omega dE_{\rm f}} &= \frac{k_{\rm f}}{k_{\rm i}} \frac{b^2}{4 \pi M} \exp(-2W) \sum_{q',p} \frac{({\bf q}'\cdot {\bf e}_{q',p})^2}{\omega_{q',p}} \sum_{j} \exp(i {\bf q} \cdot {\bf r}_j) \\ &\quad\times \int_{-\infty}^{\infty} \big[ \exp(-i {\bf q}' \cdot {\bf r}_j+i \omega_{q',p}t) (n_{q',p}+1) \nonumber \\ &\qquad\qquad+ \exp(i {\bf q}' \cdot {\bf r}_j-i \omega_{q',p}t) n_{q',p} \big] \exp(-i\omega t) dt . \nonumber \end{align} The Fourier transformations in time and space are immediately calculated, giving the final one-phonon cross section:
\begin{align} \label{eq:cross_one_phonon_QM} \frac{d^2\sigma}{d\Omega dE_{\rm f}} &= \frac{k_{\rm f}}{k_{\rm i}} \frac{b^2(2\pi)^3}{2 M V_0} \exp(-2W) \sum_{q,p,\tau} \frac{({\bf q}\cdot {\bf e}_{q,p})^2}{\omega_{q,p}} \\ &\quad\times \left[ (n_{q,p}+1) \delta(\omega-\omega_{q,p}) \delta({\bf q}-{\bf q}'+{\bf \tau}) \right. \nonumber \\ &\qquad \left. + n_{q,p} \delta(\omega+\omega_{q,p}) \delta({\bf q}+{\bf q}'+{\bf \tau}) \right] . \nonumber \end{align} This equation is essentially equal to the classical equation (\ref{eq:cross_one_phonon}), although derived in a much more rigorous way.
*Spectrometers: Instruments for inelastic neutron scattering
On instruments that use a continuous beam of neutrons, it is necessary to directly select both \(E_{\rm i}\) and \(E_{\rm f}\), in order to determine the neutron energy transfer, \(\hbar\omega\). It is here customary to use Bragg diffraction from crystals for both purposes. Such a type of instrument is denoted a triple-axis spectrometer, since the neutron changes direction by scattering three times before being detected:
- A monochromator crystal selects \(E_{\rm i}\) of the incoming beam, as discussed in Determining the incoming neutron wavelength, by Bragg scattering an angle \(2\theta_{\rm m}\).
- The sample scatters the beam by the angle \(2\theta\).
- The analyzer determines \(E_{\rm f}\) by Bragg scattering by an angle \(2\theta_{\rm a}\), in the same way as the monochromator.
The path of the neutron beam is kept in the same horizontal plane, also denoted the scattering plane. The build-up of the triple-axis spectrometer is shown in Figure xx--CrossReference--fig:tripleaxisspectrometer--xx, and the individual components of the spectrometer are listed below:
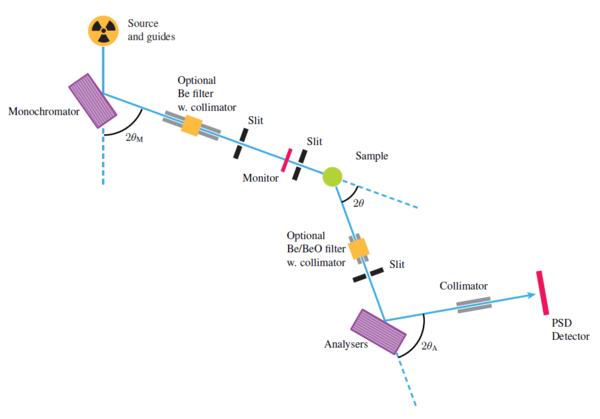
Source
The triple axis spectrometer uses a beam of cold or thermal neutrons. Most usually, a neutron guide is used to transport the beam to areas far from the source where the stray background is lower.
Monochromator
The beam is diffracted by a monochromator (see subsection Determining the incoming neutron wavelength), which selects the neutron energy, \(E_{\rm i}\), typically in the range 14-100~meV at a thermal moderator, or 2.5-14~meV for a cold moderator.
Filter
The monochromatised beam is almost always polluted with higher order scattering, from \(n>1\) in Bragg's law. A filter is used to remove these higher order scattered neutrons, either before or after the sample, or in both places.
Collimator
The monochromatic beam passes through a (often loosely collimating) horizontal Soller collimator. Collimators may also be inserted before the monochromator (rarely), between sample and analyzer (often), and after the analyzer (sometimes).
Sample
The medium-divergent, monochromatic beam hits the sample, which is often one (or several co-aligned) single crystal situated in a vacuum environment to reduce background from air scattering. In the sample, the neutrons are scattered elastically and inelastically.
Analyser
The scattered beam is again monochromatized by the analyser crystal, which works just like a monochromator, just selecting the final neutron energy, \(E_{\rm f}\). Usually, pyrolytic graphite is used for analyzer material.
Detector
The scattered neutrons are eventually detected by a single detector. This means that data on a triple-axis spectrometer are taken point by point. More advanced spectrometers may have several analyzer-detector arrangements, allowing for simultaneously detecting several points in \(({\bf q},\omega)\)-space. [2][3][4]
By correct selection of the three scattering angles, and the sample rotation, \(\omega_{\rm s}\), around a vertical axis,
the triple-axis spectrometer can be adjusted to any value of
scattering vector, \({\bf q}\), and energy transfer, \(\hbar \omega\),
allowed by the scattering condition (\ref{eq:inelastic_basic}).
In fact, \({\bf q}\) can only obtain values within the scattering plane.
This means that there are 4 free angles to determine only 3 parameters:
\(\hbar \omega\) and 2 dimensions of \({\bf q}\). In practice, this ambigiuity
is solved by fixing either \(E_{\rm i}\) or \(E_{\rm f}\) to a predetermined value.
A thorough presentation of how to perform experiments with a triple-axis spectrometer is given in Ref.~\cite{shirane}.
Experimental considerations
The 3 scattering angles, \(2\theta_{\rm m}\), \(2\theta\), and \(2\theta_{\rm a}\), are often denoted by the less-obvious symbols \(A2\), \(A4\), and \(A6\), respectively. The symbol \(A3\) denotes the sample rotation \(\omega_{\rm s}\), while the symbols \(A1\) and \(A5\) denotes the rotation of monochromator and analyzer crystals, respectively. This is also listed in table \ref{tab:As}.
Often, an experimental series consists of scans along a particular axis in \(({\bf q},\hbar\omega)\) space. One speaks about constant-energy scans and constant-q scans. For the latter, it is costumary to use a constant \(E_{\rm f}\) for the scans and then measure each scan point until a constant count number in the beam monitor has been reached. Since the sensitivity of the monitor is proportional to wavelength, \(\lambda_{\rm i}\), the number of neutrons reaching the sample for each scan point is proportional to \(1/\lambda_{\rm i}\) - or to \(k_{\rm i}\). These facts causes the factor \(k_{\rm f}/k_{\rm i}\) in the final cross section (\ref{eq:master_scatt_inel}) to be constant. Hence, the variation of this factor can be neglected, easing the subsequent data analysis.
Two types of spectrometers for a pulsed source
On instruments at pulsed sources, one can utilize time-of-flight techniques as for diffraction. However, the time-of-flight cannot be used to determine both \(E_{\rm i}\) and \(E_{\rm f}\). Either the initial or final energy must be selected by other means, typically by Bragg reflection from crystals or by chopping the beam in short time pulses close to the sample. This leads to two essentially different types of spectrometer geometries:
Direct geometry
The incoming neutrons are monochromatized by a chopper system and hits the sample in a short burst. Thus, \(E_{\rm i}\) is fixed, and the time-of-flight is used to determine the value of \(E_{\rm f}\).
Indirect geometry
The sample is hit by a "white" beam, and only outgoing neutrons with a particular energy are scattered by analyzer crystals on to the detector. Thus, \(E_{\rm f}\) is fixed and the time-of-flight is used to determine the value of \(E_{\rm i}\).
The advantages with time-of-flight spectroscopy are so large, that at many continuous sources one chooses to chop the beam close to the source, producing short pulses. In this way more than 99% of the neutrons coming through the guide system are sacrificed.
In later versions of these notes, there will be more material on time-of-flight spectrometers, including figures.
← Previous page: Quantum treatment of inelastic neutron scattering
→ Exercises: Exercises in Scattering from phonons
→ Next page: Magnetic neutron scattering
- ↑ 1.0 1.1 G.L. Squires. Thermal Neutron Scattering. Cambridge University Press, 1978.
- ↑ J.A. Rodriguez et al. Macs - a new high intensity cold neutron spectrometer at nist. Meas. Sci Techn., 19:034023, 2006.
- ↑ K. Lefmann et al. Realizing the full potential of a rita spectrometer. Physica B, 385-386:1083-1085, 2006.
- ↑ M. Kempa et al. The flatcone multianalyzer setup for ill's three-axis spectrometers. Physica B, 385-386:1080, 2006.