The neutron scattering cross section from nano-sized particles
We will now describe in mathematical terms the scattering from a system of nano-sized particles.
The cross section for neutron diffraction
Our starting point is the expression for the coherent elastic scattering cross section for a system of nuclei from the Basics of neutron scattering page,
\begin{equation}\label{dummy1945322425} \dfrac{d\sigma}{d\Omega}\biggr|_{\rm nucl.\, coh.\, el.} = \biggr|\displaystyle\sum_{j'} b_{j'} \exp(i {\mathbf q} \cdot {\mathbf r}_{j'})\biggr|^2 . \end{equation}
We have here considered the nuclei as being fixed in position. This is a very good approximation for small-angle scattering. For more details on this static approximation and on the necessary corrections to the equation, see the page on Scattering from lattice vibrations on the effect of nuclear vibrations.
The structure factor
For a sample of \(N\) nano-sized particles, we can divide the sum of the scattering nuclei into a sum over particles and a sum over the nuclei within each particle. We now write the nuclear coordinates, \({\bf r_{j}}\) in terms of the center of its host particle, \({\bf R}_J\), as \({\bf r}_{j'} \equiv {\bf r}_j + {\bf R}_J\). This gives:
\begin{align} \label{eq:sansS} \dfrac{d\sigma}{d\Omega}\biggr|_{\rm nucl.\, coh.\, el.} &= \biggr|\displaystyle\sum_{j'} b_{j'} \exp(i {\mathbf q} \cdot {\mathbf r}_{j'})\biggr|^2 \\ &= \biggr|\displaystyle\sum_{j,J} b_j \exp(i {\mathbf q} \cdot ({\mathbf R}_J + {\mathbf r}_j))\biggr|^2 \nonumber \\ &= \biggr|\displaystyle\sum_{J} \exp(i {\mathbf q} \cdot {\mathbf R}_J) \biggr|^2 \biggr| \displaystyle\sum_j b_j \exp(i {\mathbf q} \cdot {\mathbf r}_j) \biggr|^2 \nonumber \\ &\equiv N S({\mathbf q}) \biggr| \displaystyle\sum_j b_j \exp(i {\mathbf q} \cdot {\mathbf r}_j) \biggr|^2 , \nonumber \end{align}
where \(S({\bf q})\) is called the structure factor. For random, dilute systems, the relative phase between scattering from the particles, \(\exp(i {\bf q} \cdot ({\bf R}_J - {\bf R}_{K}))\), takes a random value. Hence, the interference vanishes on average, leading to \(S({\bf q})=1\). The derivation is left as an exercise to the reader, see Problem: The structure factor for dilute systems. With \(S({\bf q})\) known, the cross section from the scattering patterns is thus seen to be directly proportional to that from the individual particles.
In practice, the particles are often dispersed in a solution, which will also scatter the neutrons. This case is treated in the section SANS from particles in solution.
The small-angle approximation
We will here only consider scattering vectors of sufficiently small length, \(q\), so that the phase of the exponential, \(\bf q \cdot {\bf r}_j\), does not vary significantly between neighbouring atoms. The condition for this is
\begin{equation}\label{dummy1505234248} q a \ll 2\pi ,\, \end{equation}
where \(a\) is a typical interatomic distance. For larger values of \(q\), we are in a regime where the crystalline structure of the sample is responsible for the scattering. This leads to diffraction as will be explained in detail on the page on Diffraction from crystals.
Studying equation \eqref{eq:sansS}, we see that when the phase factor \({\bf q}\cdot {\bf r}_j\) varies insignificantly between neighbouring nuclei, the scattering from the individual nuclei cannot be distinguished, and the sample scatters approximately as a continuum. Hence it becomes valid to transform the sum in equation \eqref{eq:sansS} into an integral
\begin{equation}\label{eq:sans_sum} \displaystyle\sum_j b_j \exp(i \mathbf q \cdot {\mathbf r}_j) \longrightarrow \displaystyle\int_V \rho_b \exp(i \mathbf q \cdot {\mathbf r}) dV , \end{equation}
where \(\rho_b\) is the effective scattering length density for the sample. The scattering length density is defined as the sum of the coherent scattering lengths over all atoms within a given volume, \(V_0\), divided by this volume,
\begin{equation}\label{eq:rho} \rho_b = \dfrac{1}{V_0} \displaystyle\sum_{j \in V_0} b_{j} , \end{equation}
where \(j\) represents the position of the nuclei in the volume (which could be a formula unit). After the transformation, the SANS cross section reads
\begin{equation}\label{eq:SANS_cross} \dfrac{d\sigma}{d\Omega} \biggr|_{\rm SANS} = N S({\mathbf q}) \left| \displaystyle\int \rho_b({\mathbf r}) \exp(i \mathbf q \cdot {\mathbf r}) dV \right|^2 . \end{equation}
Experimental considerations
In a typical SANS experiment \(q\leq q_{\rm max} = \leq 0.3\) Å\(^{-1}\). Hence, only structures larger than around \(2\pi /q_{max}\approx 20\) Å are well resolved.
Instruments specialized in SANS can also be used to study periodic (crystalline) arrangements where the period is larger than the typical 2-10 Å, known from simple crystal structures. This could be crystals of very large molecules, superstructures, magnetic structures with long repetition length, etc.
SANS from particles in solution
One of the main applications of SANS is the study of nano-sized objects, suspended in a solution. In practice, the objects could be polymers or micelles, described in the Applications of SANS in nanoscience section, and the solvent could be water or an organic liquid.
As a start, we first consider one single nano-sized particle. For the combined system, it is convenient to separate the volume integration into an integral over the particle and an integral over the solvent,
\begin{equation}\label{dummy776960957} \dfrac{d\sigma}{d\Omega} \biggr|_{\rm SANS,\, 1\, particle} = \left| \displaystyle\int_{\rm particle} \rho_b({\mathbf r}) \exp(i \mathbf q \cdot {\mathbf r}) dV + \rho_s \displaystyle\int_{\rm solvent} \exp(i \mathbf q \cdot {\mathbf r}) dV\right|^2 . \end{equation}
By using the scattering length density contrast,
\begin{equation}\label{dummy1510031759} \Delta\rho({\mathbf r}) = \rho_b({\mathbf r}) - \rho_s, \end{equation}
the solvent integration is replaced by an integration over the entire sample volume, \(V_{\rm s}\),
\begin{equation}\label{dummy671100274} \dfrac{d\sigma}{d\Omega}\biggr|_{\rm SANS,\, 1\, particle} = \left| \displaystyle\int_{\rm particle} \Delta\rho({\mathbf r}) \exp(i \mathbf q \cdot {\mathbf r}) dV + \rho_s \displaystyle\int_{V_{\rm s}} \exp(i \mathbf q \cdot {\mathbf r}) dV\right|^2 . \end{equation}
Typically, the sample dimensions are of the order mm. This is roughly 4-6 orders of magnitude larger than the length scale of typical nano-sized particles. Hence, the contribution to small-angle scattering from the entire volume \(V\) is almost a \(\delta\)-function in \(q\) - or to be more accurate has a width of the order \(10^{-6}\) Å\(^{-1}\). Such low \(q\)-values are not at all visible in the SANS measurements, where the typical minimum scattering vector is \(q_{min} \approx 10^{-3}\) Å\(^{-1}\). We can therefore neglect the total volume scattering. Taking into account that the sample consists of \(N\) particles, the scattering cross section reads
\begin{equation}\label{dummy177978770} \dfrac{d\sigma}{d\Omega} \biggr|_{\rm SANS,\, particles} = N S({\mathbf q}) \left| \displaystyle\int_{\rm particle} \Delta\rho({\mathbf r}) \exp(i \mathbf q \cdot {\mathbf r}) dV \right|^2 . \end{equation}
Notice that the scattering cross section depends essentially on the square of the contrast in scattering length density. Hence, the scattered intensity can be changed strongly by, e.g., varying the scattering length density of the solvent. This is typically done by deuteration, as illustrated in the "five reasons" figure on the Introduction to neutron scattering page.
In a different formulation, we describe the scattering in terms of the particle density \(n = N/V_{\rm s}\) and the volume specific cross section \(\Sigma = \sigma / V_{\rm s}\). The volume specific differential scattering cross section then becomes
\begin{equation}\label{eq:SANScross} \dfrac{d\Sigma}{d\Omega} \biggr|_{\rm SANS,\, particles} = n S({\mathbf q}) \left| \displaystyle\int_{\rm particle} \Delta\rho({\mathbf r}) \exp(i \mathbf q \cdot {\mathbf r}) dV \right|^2 . \end{equation}
The particle form factor
For monodisperse, homogeneous particles, the cross section equation \eqref{eq:SANScross} simplifies to
\begin{equation}\label{dummy497150881} \dfrac{d\Sigma}{d\Omega} \biggr|_{\rm SANS,\, simple} = n \Delta\rho^2 S({\mathbf q}) \left| \displaystyle\int_{\rm particle} \exp(i \mathbf q \cdot {\mathbf r}) dV \right|^2 , \end{equation}
leading to
\begin{equation}\label{eq:SANScross2} \dfrac{d\Sigma}{d\Omega} \biggr|_{\rm SANS,\, simple} \equiv n \Delta\rho^2 V^2 S({\mathbf q}) P(\mathbf q), \end{equation}
where \(V\) is the particle volume and \(P(\mathbf q)\) is known as the particle form factor,
\begin{equation}\label{eq:sans_formfactor} P(\mathbf q)= \left| \dfrac{1}{V} \displaystyle\int dV e^{i \mathbf q \cdot {\mathbf r}} \right|^2 , \end{equation}
which takes its maximum value of 1 as \(q \rightarrow 0\).
When defining the particle volume fraction as \(\phi=NV/V_{\rm s} = nV\), the cross section reads
\begin{equation}\label{eq:SANScross_phi} \dfrac{d\Sigma}{d\Omega} \biggr|_{\rm SANS,\, simple} \equiv \phi \Delta\rho^2 V S({\mathbf q}) P({\mathbf q}). \end{equation}
Sometimes in the SANS literature, the volume specific cross section is denoted loosely \(I(\mathbf q) = d\Sigma/d\Omega\), as if it was the observed intensity.
The form factor of a solid sphere
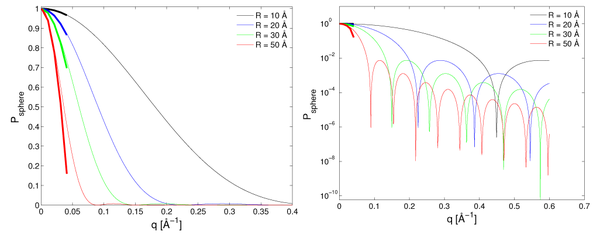
For a solid sphere of radius \(R\), the form factor is isotropic and is easily calculated (see the problem Scattering form factor for spheres). The result is
\begin{equation}\label{eq:sans_spheres} P_{\rm sphere}(q)= \left( 3 \, \dfrac{\sin(q R)-q R \cos(q R)} {(q R)^3}\right)^2 , \end{equation} which is illustrated for different radii in Figure xx--CrossReference--fig:solidsphereformfactor--xx.
The form factor of a spherical shell
From the calculations leading to the form factor for a sphere \eqref{eq:sans_spheres}, it is straight-forward to show that the form factor amplitude for a thin spherical shell is:
\begin{equation} \label{eq:shell_form} P_{\rm shell}(q) = \left( \frac{\frac{4\pi}{3}R_{\rm out}^3P_{\rm sphere}(qR_{\rm out})-\frac{4\pi}{3}R_{\rm in}^3 P_{\rm sphere}(qR_{\rm in})}{\frac{4\pi}{3}(R_{\rm out}^3-R_{\rm in}^3)} \right)^2 , \end{equation}
where \(R_{\rm out}\) is the outer radius of the shell and the inner radius of the shell is \(R_{\rm in}=R_{\rm out} -D\), and \(D\) is the thickness of the shell. There, \(P_{\rm sphere}(qr)\) is here the form factor of a sphere \eqref{eq:sans_spheres}, as calculated in Scattering form factor for spheres.
The calculation leading to this result comes directly by expanding \eqref{eq:sans_formfactor}, using \eqref{eq:debye},
\begin{align} P(\mathbf q) &= \left| \frac{1}{V} \int dV e^{i \mathbf q \cdot {\bf r}} \right|^2 = \frac{(4\pi)^2}{V^2} \left| \int_{R_{\rm in}}^{R_{\rm out}} r^2 \frac{\sin(qr)}{qr} dr \right|^2 \nonumber \\ &= \left( \frac{3}{q^3 (R_{\rm out}^3-R_{\rm in}^3)} \right)^2 \left| \int_{qR_{\rm in}}^{qR_{\rm out}} (rq) \sin(rq) d(rq) \right|^2 \nonumber \\ &= \left( \frac{R_{\rm out}^3 P_{\rm sphere}(qR_{\rm out}) - R_{\rm in}^3 P_{\rm sphere}(qR_{\rm in})}{R_{\rm out}^3 - R_{\rm in}^3} \right)^2 . \end{align}
Polydispersity
Above, we have considered monodisperse (identical) particles only. If, however, the particles in the thin solution are not all the same size, we denote them polydisperse, and we ascribe them a size distribution, \(D(R)\), defined as the probability of finding a particle of size \(R\). Since \(D(R)\) is a probability, \(\int D(R) dR = 1\). For dilute, polydisperse particles, the form factor in equation \eqref{eq:sans_formfactor} is modified according to
\begin{equation}\label{dummy961841526} P(q)=\displaystyle\int {\rm d} R\ D(R)\ P(q,R) . \end{equation}
Hence the total SANS cross section per sample volume is
\begin{equation}\label{dummy1724599799} \dfrac{d\Sigma}{d\Omega}(q)=n (\Delta \rho)^2 \displaystyle\int {\rm d} R\ V(R)\ D(R)\ P(q,R) , \end{equation}
where \(P(q,R)\) is the size-dependent form factor and \(V(R) = (4\pi/3)R^3\).
One of the most simple - but not generally the most correct - ways of including the structure factor is by using the so-called locally monodisperse approximation [1], where we approximate the particle volume, \(V(R)\), by its average value, \(V=(4\pi/3) R_{\rm av}^3\), to reach
\begin{equation} \label{dummy17245997994342412} \frac{d\Sigma}{d\Omega}(q)=n V (\Delta \rho)^2 \int {\rm d} R \ D(R)\ P(q,R) , \end{equation}
As the concentration of particles increases, the inter-particle interaction becomes increasingly important. Hence, the structure factor \(S(q,R)\) can no longer be considered to be unity. The total SANS cross section per sample volume can then be written
\begin{equation} \label{eq:local_mono} \dfrac{d\Sigma}{d\Omega}(q)=n V (\Delta \rho)^2 \displaystyle\int {\rm d} R\ D(R) P(q,R) S(q,R) . \end{equation}
The effect of polydispersity will be explored in the problem Polydisperse spheres.
Complementarity of neutrons and X-rays
SANS is often used in combination with its sister technique, Small-Angle X-ray Scattering (SAXS), and the fundamental theories for SANS and SAXS are very similar. In addition, the experimental setup of a SAXS instrument is in principle very similar to that of the SANS instrument. The main difference between the two methods is that in SANS, the incoming neutrons are scattered by the nuclei of the studied sample, whereas in SAXS the incoming photons are scattered by the electrons.
The scattering length of an electron, \(b_{\rm e}\) is given by the classical electron radius (also known as the Compton radius or the Thompson scattering length). It is given by \(b_{\rm e}= r_0 = e^2/(4 \pi \varepsilon_0 m_{\rm e} c^2)= 2.82\) fm, where \(\varepsilon_0\) is the vacuum permittivity, \(e\) and \(m_{\rm e}\) are the charge and mass of the electron, and \(c\) is the speed of light. Thus the scattering length of an atom with atomic number \(Z\) is simply \(Z b_{\rm e}\).
SAXS has a major advantage in the easy access to very intense, well-collimated and well-focused X-ray beams, both in home-based laboratories and at large scale synchrotron facilities.
As mentioned on the Introduction page, the major advantage of SANS as compared to SAXS is the access to contrast variation via the exploitation of the difference in scattering length between hydrogen (H) and deuterium (D). This opens up for systematic contrast variation SANS measurements, where domains of specific interest in the system under investigation are enhanced at the same time as other domains are made practically invisible. This opportunity is widely applied within the investigation of biological and other organic materials. The contrast variation SANS approach has been used for investigating the internal organization of large protein complexes, to determine the finer details of phospholipid membranes, and to obtain insight into the conformation of the single polymer-chains in soft condensed materials.
- ↑ J.S. Pedersen. J. Appl. Cryst. 27 (1994), p. 595-608