Basics of neutron scattering

This chapter contains the basics of scattering theory. The present description is specialised to neutron scattering, but is in general valid also for scattering of other types of radiation, like electrons or X-rays.

In the process we describe in the main part of this chapter, neutrons are scattered by the nuclei by the strong nuclear forces. The range of these forces are femtometers (fm), much smaller than the neutron wavelength (measured in Å). Thus, the neutron cannot probe the internal structure of the nucleus, and the scattering from a single nucleus is isotropic. In contrast, in the last section of the chapter, we describe the scattering of neutrons due to magnetic forces, which are of the Å range. For this reason, magnetic neutron scattering is not isotropic.

The contents of this chapter form the basis for the understanding of the later parts of these notes, in particular elastic and inelastic neutron scattering from particles, surfaces, powders, and crystals, as well as measurements of transmission through solid objects, also known as imaging.

The process of neutron scattering is unavoidably of quantum mechanical nature. However, most of this chapter is kept less rigorous, since for many applications a full formal treatment is unnecessary. Although vastly different, these two approaches lead (in this case) to identical results. More strict, quantum mechanical derivations of the central expressions in this chapter are given in chapter 3.

The neutron cross sections

We fist introduce the terms by which we describe the scattering of a neutron beam. In particular, we describe the interaction of a neutron beam with materials by introducing the central concept of cross sections.

Neutron flux

We define the flux of a neutron beam as the neutron rate per area

\begin{equation}\label{dummy378179674} \Psi = \dfrac{ {\rm number\; of\; neutrons\; impinging\; on\; a\; surface\; per\; second}} { {\rm surface\; area\; perpendicular\; to\; the\; neutron\; beam\; direction}} , \end{equation}

usually given in the unit n/(cm\(^2\)s).

Experimental considerations

At most neutron scattering experiments, the incoming flux at the sample position lies in the range \(10^4\) to \(10^9\) n/(cm\(^2\)s). At ESS, however, some instruments will reach a flux of \(10^{10}\) n/(cm\(^2\)s).

The scattering cross section

The neutron scattering cross section, \(\sigma\), of a system is defined by the system's ability to scatter neutrons:

\begin{equation}\label{eq:sigma_def} \sigma = \dfrac{1}{\Psi} \cdot { {\rm number\; of\; neutrons\; scattered\; per\; second}} , \end{equation}

which has units of area. The scattering intensity is divided by the neutron flux to ensure that \(\sigma\) is an intrinsic property, independent on the neutron flux at the particular experimental set-up.

For a single nucleus, \(\sigma\) can now be seen as the effective area of the nucleus perpendicular to the neutron beam, as will be elaborated in the problem the cross section. The scattering cross section used here is the total cross section, which depends on the system (sample) volume, \(V\). For thin samples, \(\sigma\) can be described by the volume specific cross section, \(\Sigma\), through

\begin{equation}\label{eq:Sigma_def} \sigma = V \Sigma .\, \end{equation}

For thicker samples, beam attenuation must be taken into account; see the section Beam attenuation due to scattering.

The differential scattering cross section

The angular dependence of the scattered neutrons is a most important aspect of all neutron scattering. To describe this dependence, we define the differential scattering cross section as the intensity of neutrons scattered into a particular solid angle, \(d\Omega\). We denote the wave vector of the incoming neutron by \(k_i\) and that of the outgoing neutron by \(k_f\), where the indices "i" and "f" denote initial and final, respectively. This is illustrated in Figure xx--CrossReference--fig:Fig2dot1v3.png--xx and is quantified as:

Figure 1: An illustration of the scattering geometry. The incoming neutrons, labeled \(k_i\), scatter at the center of the sphere with the scattering angle \(2\theta\) and azumital angle \(\phi\). The neutrons scattered into the solid angle element \(d\Omega\) (or detector area \(dA\) ar labeled with \(k_f\).

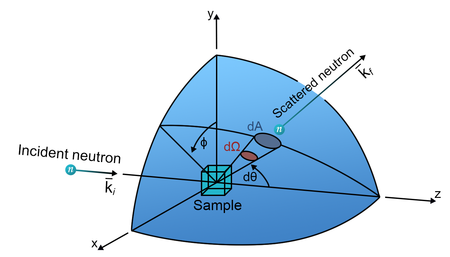
\begin{equation}\label{eq:dscs} \frac{d\sigma}{d\Omega} = \frac{1}{\Psi} \frac{{\rm \; number\; of\; neutrons\; scattered \; into\; solid\; angle\;} d\Omega{\rm \; per\; second}}{d\Omega} . \end{equation}

The total number of scattered neutrons is the integral of neutrons per solid angle over all of the \(4\pi\) solid angle, hence

\begin{equation}\label{eq:dscs_int} \sigma = \displaystyle\int \dfrac{d\sigma}{d\Omega} d\Omega . \end{equation}

The partial differential scattering cross section

In some scattering processes, the neutron delivers energy to or absorbs energy from the scattering system. This type of scattering we denote inelastic scattering. We define the neutron energy transfer by

\begin{equation}\label{eq:inelastic_basic} \hbar \omega = E_{\rm i} - E_{\rm f}, \end{equation}

which can also be written as

\begin{equation}\label{eq:inelastic_basic2} \hbar \omega = \dfrac{\hbar^2(k_{\rm i}^2-k_{\rm f}^2)}{2 m_{\rm n}}. \end{equation}

Note that the energy change is defined with the opposite sign of most definitions of changing properties, so that neutron energy loss gives a positive value of \(\hbar \omega\), while neutron energy gain gives negative values.

In inelastic scattering processes, energy is transfered to - or taken from - the sample. Energy conservation gives that the energy change, \(\Delta E\), of the sample is given by

\begin{equation}\label{dummy1737456334} \Delta{}E = \hbar \omega . \, \end{equation}

For describing inelastic scattering, one needs to take into account the energy dependence of the scattered neutrons. This is described by the partial differential scattering cross section:

\begin{equation}\label{eq:pdscs} \dfrac{d^2\sigma}{d\Omega dE_{\rm f}} = \dfrac{1}{\Psi} \dfrac{ { {\rm number\; of\; neutrons\; scattered\; per\; sec.\; into\;}} d\Omega\; { {\rm with\; energies\;}} [ E_{\rm f};E_{\rm f}+dE_{\rm f} ] } {d\Omega dE_{\rm f}} . \end{equation}

Integrating over the all final energies, \(E_{\rm f}\), we reach the differential cross section described earlier:

\begin{equation}\label{dummy222151533} \dfrac{d\sigma}{d\Omega} = \displaystyle\int \dfrac{d^2\sigma}{d\Omega dE_{\rm f}} dE_{\rm f}. \end{equation}

Following equation \eqref{eq:dscs_int}, the total cross section is found by a double integration:

\begin{equation}\label{dummy350986584} \sigma = \displaystyle\iint \dfrac{d^2\sigma}{d\Omega dE_{\rm f}} d\Omega dE_{\rm f}. \end{equation}

For a closer description of inelastic scattering, a quantum mechanical treatment of the scattering process is required, as initiated in the section Quantum mechanics of scattering and described in detail in the part on dynamics of materials.

The absorption cross section

Neutron absorption takes place as a result of neutron-induced nuclear processes, which destroy the neutrons, emitting secondary radiation (\(\alpha\), \(\beta\), or \(\gamma\)) as a result. In most cases, the absorption cross section, \(\sigma_{\rm a}\), of thermal neutrons is inversely proportional to the neutron velocity. In other words, the absorption is proportional to the neutron wavelength: \(\sigma_{\rm a} \propto \lambda\).

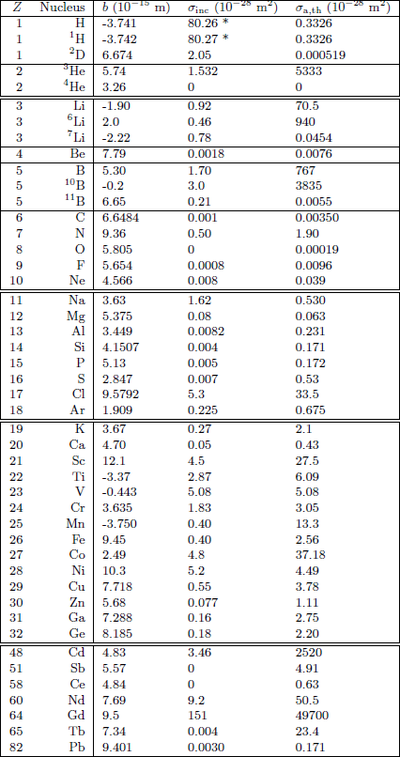
The neutron absorption cross sections are measured and tabelized for all but the rarest isotopes, see e.g. the Neutron Data Booklet, or the NIST home page. Traditionally, the absorption cross section of isotope \(j\) is given as \(\sigma_{\text{a,j,th}}\) per nucleus in units of "barns" (1 barn \(=10^{-28}\) m\(^{2}\)) and is listed at the standard "thermal" velocity \(v_\text{th} = 2200\) ms\(^{-1}\) (\(\lambda_\text{th} = 1.7982\) Å, see also the neutron unit conversion table on the Introduction to neutron scattering page). The actual absorption cross section is then given by

Table 1: Neutron cross sections and scattering lengths for the first 32 elements (isotopic average using the natural abundancies). In addition, data for selected isotopes and for some heavier elements are presented. Data taken from . * It should be noted that the important incoherent cross section for H varies with neutron wavelength. The value listed is valid for \(\lambda > 1.798\) Å

\begin{equation}\label{dummy2114890051} \sigma_{\rm a,j} = \sigma_{\text{a,j,th}} \dfrac{v_\text{th}}{v} = \sigma_{\text{a,j,th}} \dfrac{\lambda}{\lambda_\text{th}}. \end{equation}

Also for absorption, the volume specific cross section is defined as

\begin{equation}\label{dummy21148900512} \sigma_{\rm a,j} = V \Sigma_{\rm a,j}. \end{equation}

In a general material, many nuclei contribute to the total absorption. As in equation \eqref{eq:attenuation}, the resulting attenuation coefficient is

\begin{equation}\label{dummy74943618} \Sigma_{\rm a} = \sum_j \dfrac{N_j \sigma_{ {\rm a},j}}{ V} = \sum_j n_j \sigma_{ {\rm a},j}. \end{equation}

In this sum, \(N_j\) represents the number of nuclei of isotope, \(j\) in the sample volume \(V\), and \(n_j=N_j/V\) is their respective atomic density.

An abbreviated list of absorption and scattering cross sections for selected isotopes/elements is given in Table xx--CrossReference--tab:cross--xx.

Wave description of nuclear scattering

In this section, we discuss the basics of scattering of (neutron) waves, from a semi-classical point of view.

The neutron wave

The incoming (or initial) neutron can be described as a (complex) plane wave

\begin{equation}\label{eq:initialwave} \psi_{\rm i}({\mathbf r}) = \dfrac{1}{\sqrt{Y}} \exp(i {\mathbf k}_{\rm i} \cdot {\mathbf r}) , \end{equation}

where \(Y\) is a normalization constant, implying that the density of the incoming neutron wave is \(|\psi_{\rm i}|^2=1/Y\). This has no implication on the final results, since \(Y\) will eventually cancel in the final equations, but we keep the normalization for completeness. We have in \eqref{eq:initialwave} omitted an explicit time dependence, \(\exp(-i\omega t)\), which plays no role until we discuss inelastic scattering in part IV.

From the equation defining the wavenumber \(\bf k\) on the page Introduction to neutron scattering, the velocity of a neutron described by a plane wave is

\begin{equation}\label{eq:neutron_v} v= \dfrac{\hbar k_{\rm i}}{ m_{\rm n} }. \end{equation}

Similarly, the corresponding incoming neutron flux is

\begin{equation}\label{eq:flux_plane} \Psi_{\rm i} = |\psi_{\rm i}|^2 v = \dfrac{1}{Y} \dfrac{\hbar k_{\rm i}}{m_{\rm n}} . \end{equation}

We will use this result as a stepping stone in the following calculations.

Elastic neutron scattering from a single nucleus

We consider the idealized situation where a neutron with a well defined velocity is scattered by a single nucleus, labeled \(j\), which is (somehow) fixed in position. The scattered neutron can be described as a spherical wave leaving the nucleus, which is centered at \({\bf r}_j\), as shown in Figure xx--CrossReference--fig:1nucleus--xx. The scattered, or final, wave reads:

\begin{equation}\label{eq:scatter_wave} \psi_{\rm f}({\mathbf r}) = \psi_{\rm i}({\mathbf r}_j) \dfrac{-b_j}{|{\mathbf r}-{\mathbf r}_j|} \exp(i k_{\rm f} |{\mathbf r}-{\mathbf r}_j|), \end{equation}

where \(b_j\) is a quantity characteristic for the particular isotope. Since \(b_j\) has the unit of length, it is usually denoted scattering length and is typically of the order 1-10 fm. This above equation is valid only "far" from the nucleus, i.e. for \(|{\bf r}-{\bf r}_j| \gg b_j\). The minus sign in equation \eqref{eq:scatter_wave} is a convention chosen so that most nuclei will have a positive value of \(b_j\).

Figure 2: An illustration of the initial wave, \(\psi_{\rm i}\), of wavelength \(\lambda_{\rm i}\), and the final wave, \(\psi_{\rm f}\), of wavelength \(\lambda_{\rm f}\), describing a neutron scattering off a single nucleus with positive scattering length (meaning a phase shift of \(\pi\)). The area, \(dA\), for measuring the flux of the outgoing neutrons is the detector area as sketched.

In experiments, \(r\) is typically of the order 1 m. For convenience, we will position the Origo close to the centre of the "relevant" part of the sample. Hence, the nuclear coordinate, \(r_j\), is typically of the order 1 mm or less, and the density of outgoing neutrons can be approximated by \(|\psi_{\rm f}|^2 \approx b_j^2/(Y r^2)\), omitting \({\bf r}_j\) in the denominator of \eqref{eq:scatter_wave}. The number of neutrons per second intersecting a small surface, \(dA\), is \(v |\psi_{\rm f}|^2 dA = v b_j^2/(Yr^2) dA\). Using equation \eqref{eq:neutron_v} and the expression for solid angle \(d\Omega = dA/r^2\), we reach

\begin{equation}\label{dummy854759296} {\rm number\; of\; neutrons\; per\; second\; in\;} d\Omega = \dfrac{1}{Y} \dfrac{b_j^2 \hbar k_{\rm f}}{m_{\rm n}} d\Omega. \end{equation}

Since the scattering nucleus is fixed, energy conservation requires that the energy of the neutron is unchanged. In this so-called elastic scattering, we therefore have \(k_{\rm i} = k_{\rm f}\). Using equation \eqref{eq:dscs} and \eqref{eq:flux_plane}, this leads to the simple expression for the differential cross section for one nucleus:

\begin{equation}\label{eq:nuclear_diff_cross} \dfrac{d\sigma}{d\Omega} = b_j^2 , \end{equation}

giving the total scattering cross section of

\begin{equation}\label{eq:nuclear_cross} \sigma = 4 \pi b_j^2 . \end{equation}

Scattering from two nuclei - interference

In the field of neutron scattering from materials, we are concerned with the effect of scattering from a system of particles, instead of just one. We therefore begin to add complexity by considering the scattering from two nuclei, again placed at fixed positions. This simple system will reveal some very important features, which we will utilize later.

The neutron wave that is scattered from the two nuclei is in fact describing just one single neutron. Nevertheless, this neutron "senses" the presence of both nuclei, meaning that the wave amplitude scattered from one nucleus will add to the wave amplitude scattered from another nucleus. This interference is a central aspect in most scattering techniques.

We assume that the incoming neutron wave at the position of the second nucleus is not notably attenuated by the scattering of the first nucleus, and vice versa. This is known as the Born Approximation.

Let us describe the situation in more precise terms. We assume elastic scattering, \(k_{\rm i} = k_{\rm f} \equiv k\) and we denote the nuclear scattering lengths as \(b_j\) and \(b_{j'}\), respectively. Generalizing equation \eqref{eq:scatter_wave}, the outgoing (final) wave can be described as

\begin{equation}\label{dummy566330241} \psi_{\rm f}({\mathbf r}) = - \left( b_j \dfrac{\psi_{\rm i}({\mathbf r}_j)}{|{\mathbf r}-{\mathbf r}_j|} \exp(i k_f |{\mathbf r}-{\mathbf r}_j|) + b_{j'} \dfrac{\psi_{\rm i}({\mathbf r}_{j'})}{|{\mathbf r}-{\mathbf r}_{j'}|} \exp(i k_f |{\mathbf r}-{\mathbf r}_{j'}|) \right) , \end{equation}

where \(\psi_{\rm i}({\bf r})\) is the plane wave given by equation \eqref{eq:initialwave}. The two nuclei are assumed to be closely spaced compared with the distance to the observer: \(|{\bf r}_j - {\bf r}_{j'}| \ll r\). Choosing the origin to lie close to the two particles, the denominators can be considered equal, giving

\begin{equation}\label{eq:interference1} \psi_{\rm f}({\mathbf r}) = - \dfrac{1}{\sqrt{Y}} \dfrac{1}{r}\big[ b_j \exp(i {\mathbf k}_{\rm i}\cdot {\mathbf r}_j) \exp(i k_f |{\mathbf r}-{\mathbf r}_j|) + b_{j'} \exp(i {\mathbf k}_{\rm i}\cdot {\mathbf r}_{j'}) \exp(i k_f |{\mathbf r}-{\mathbf r}_{j'}|) \big] \end{equation}

In contrast to the "sloppy" treatment of the distance \(r\), we need to very accurately keep track of the length \(|{\bf r}-{\bf r}_j|\), since it enters in the phase of the complex wave function. It is convenient to write the nuclear coordinate, \({\bf r}_j\), as the sum of a component parallel to and a component perpendicular to \({\bf r}\):

\begin{equation}\label{dummy801871315} |{\mathbf r}-{\mathbf r}_j| = |{\mathbf r}-{\mathbf r}_{j,||}-{\mathbf r}_{j,\perp}| = \sqrt{\left|{\mathbf r}-{\mathbf r}_{j,||}\right|^2+\left|{\mathbf r}_{j,\perp}\right|^2} , \end{equation}

where the last step is due to Pythagoras. The last term in the square root is by far the smallest and vanishes to first order. To check the order of magnitude of the second order correction, we take a "large" distance between nuclei of \(|r_j| \approx 1\,\mu\)m and \(|{\bf r}-{\bf r}_{j,||}| \approx 1\) m. This gives an error in the approximation of \(\approx 0.005\) Å; much smaller than the typical neutron wavelength we consider. This means that effectively only one nuclear coordinate, \({\bf r}_{j,||}\), contributes and that the square root can be lifted to give \(|{\bf r}-{\bf r}_j|=|{\bf r}-{\bf r}_{j,||}|\). Now, we can write

\begin{equation}\label{eq:scalar_to_dot} k_f |{\mathbf r} - {\mathbf r}_{j,||}| = {\mathbf k}_{\rm f} \cdot ({\mathbf r} - {\mathbf r}_{j,||}), \end{equation}

where \({\bf k}_{\rm f}\) is a wave vector with length \(k_{\rm f}\) (which here equals \(k\)), oriented parallel to \({\bf r}\). Since \({\bf k}_{\rm f} \cdot {\bf r}_{j,\perp} = 0\), we have \({\bf k}_{\rm f} \cdot {\bf r}_{\rm j,||} = {\bf k}_{\rm f} \cdot {\bf r}_{\rm j}\). We insert this in the right side of \eqref{eq:scalar_to_dot} and take the complex exponential, reaching

\begin{equation}\label{dummy1462842445} \exp(i k_f |{\mathbf r}-{\mathbf r}_j|) = \exp(i {\mathbf k}_{\rm f} \cdot ({\mathbf r}-{\mathbf r}_j)). \end{equation}

Rearranging terms, the final wave can be written as

\begin{equation}\label{dummy906628448} \psi_{\rm f}({\mathbf r}) = -\dfrac{1}{\sqrt{Y}} \dfrac{1}{r}\exp(i{\mathbf k}_{\rm f}\cdot{\mathbf r}) \left[ b_j \exp(i ({\mathbf k}_{\rm i}-{\mathbf k}_{\rm f})\cdot {\mathbf r}_j) + b_{j'} \exp(i ({\mathbf k}_{\rm i}-{\mathbf k}_{\rm f})\cdot {\mathbf r}_{j'}) \right] . \end{equation}

This shows that the observer at position \({\bf r}\) will experience a scattered neutron wave that locally seems like a plane wave with wavevector that is parallel to ${\bf r}$.

The intensity of neutrons impinging on a small area is again given as \(v |\psi_{\rm f}({\bf r})|^2 dA\). Hereby we can write the scattering intensity as

\begin{equation}\label{dummy1518846130} {\rm number\; of\; neutrons\; per\; second\; in\;} d\Omega = \dfrac{1}{Y} \dfrac{\hbar k_{\rm f}}{m_{\rm n}} d\Omega \left| b_j \exp(i \mathbf{q} \cdot {\mathbf r}_j) + b_{j'} \exp(i \mathbf{q} \cdot {\mathbf r}_{j'}) \right|^2 , \end{equation}

where we have defined the very central concept of neutron scattering, the scattering vector, as

\begin{equation}\label{dummy903425712} \mathbf{q} = {\mathbf k}_{\rm i} - {\mathbf k}_{\rm f} . \end{equation}

The final expression for the differential scattering cross section for elastic scattering from nuclei now becomes:

\begin{equation}\label{eq:interference2} \dfrac{d\sigma}{d\Omega} = b^2 \big|\exp(i \mathbf{q} \cdot {\mathbf r}_j) +\exp(i \mathbf{q} \cdot {\mathbf r}_{j'})\big|^2 = 2 b^2 \big( 1 + \cos[\mathbf{q} \cdot ({\mathbf r}_j-{\mathbf r}_{j'})] \big) . \end{equation}

At some values of \(\mathbf{q}\), we have \(\cos[\mathbf{q} \cdot ({\bf r}_j-{\bf r}_{j'})] = -1\), meaning that the waves from the two nuclei are in counter phase and that the cross section thus vanishes. At other values of \(\mathbf{q}\), the scattering is in phase, \(\cos[\mathbf{q} \cdot ({\bf r}_j-{\bf r}_{j'})] = 1\), giving a value of the cross section of \(4b^2\), which is four times the cross section of a single nucleus (\(b^2\)). This enhancement of the signal is the essence of interference.

Coherent elastic scattering from a system of nuclei

In neutron scattering, we deal with interference between waves scattered from a large number of nuclei in the same way as we have seen for two nuclei above. Fortunately, the principle of interference applies equally well to many particles as to two. For this reason, we can simply generalize equation (\ref{eq:interference2}) to contain several particles \begin{equation} \label{eq:diffraction} %Squires never writes this - strange! \left.\frac{d\sigma}{d\Omega}\right|_{\rm coh} = \biggr|\sum_j b_j \exp(i {\bf q} \cdot {\bf r}_j)\biggr|^2 \, . \end{equation} This is a very important result, which is used in most types of neutron scattering.

Figure 3: Illustration of the scattering process with the incoming and outgoing beam, the wave vectors, \({\bf k}_{\rm i}\) and \({\bf k}_{\rm f}\), and the scattering vector \({\bf q}\).

Experimental considerations

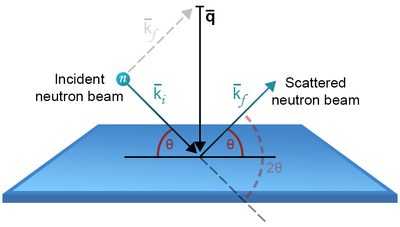
In a scattering experiment, one will always measure the scattering angle with respect to the incoming beam, as illustrated in Figure xx--CrossReference--fig:theta_2theta--xx. The scattering angle is known as \(2\theta\). In elastic scattering, \(k_{\rm i}=k_{\rm f} \equiv k\), and we can see from the figure that

\begin{equation} \label{eq:Bragg_ktoq} %(S3.51) q = 2 k \sin(\theta) \, \end{equation}

or the often presented alternative

\begin{equation} \label{eq:Bragg_lambdatoq} q = 4 \pi \sin(\theta) / \lambda \, . \end{equation}

Coherent and incoherent scattering

Very often, the neutron scattering length varies from nucleus to nucleus in a sample. This can be caused by the variation of the nuclear spin direction with time, or by variations between isotopes of the same element - or between different elements. We here describe how this affects the scattering cross sections.

The coherent and incoherent cross sections

We will here consider what happens to the scattering cross section if the nuclear scattering lengths vary randomly within the sample.

Variation in scattering lengths

We have to types of variation in nuclear scattering length: Element or isotope disorder, which is a static effect, and variations in the value of \(b_j\) themselves due to variations in the nuclear spin directions, which is a dynamic effect. However, for a macroscopic sample the calculations can be treated in the same way, since we can assume that 1) the sample is large enough to essentially represent an ensemble average and 2) we observe the system over times much longer than nuclear fluctuation times, meaning that the time average equals an ensemble average.

Let us for simplicity assume that the scattering length at site \(j\) has the stochastic value

\begin{equation} \label{eq:b_av} b_j=\langle b_j \rangle + \delta b_j , \end{equation}

where \(\langle b_j \rangle\) denotes the (time and ensemble) average. \(\delta b_j\) is the local deviation from the average, defined so that \(\langle \delta b_j \rangle = 0\). We assume that the deviations are uncorrelated between sites, \(\langle \delta b_j \, \delta b_{j'} \rangle = 0\).

To derive the mean differential scattering cross section, it is sufficient to consider the two-atom problem.

\begin{equation} \label{eq:sigma_av} \left\langle \dfrac{d\sigma}{d\Omega}\right\rangle = \left\langle|b_j \exp(i \mathbf{q}\cdot {\mathbf r}_j) + b_{j'}\exp(i \mathbf{q}\cdot {\mathbf r}_{j'})|^2 \right\rangle = \left\langle|b^2_j + b^2_{j'} + 2b_j b_{j'} cos({\bf q} \cdot ({\bf r}_j - {\bf r}_{j'})) \right\rangle \end{equation}

Using (\ref{eq:b_av}), we now see that the "square terms" in \eqref{eq:sigma_av} give \(\langle b_j^2 \rangle = \langle b_j \rangle ^2 + \langle \delta b_j^2 \rangle\), because \( \langle \langle b_j \rangle \delta b_j \rangle = \langle b_j \rangle \langle \delta b_j \rangle \). In a similar way, the "interference terms" are seen to give \(\langle b_j b_{j'} \rangle = \langle b_j\rangle \langle b_{j'}\rangle\). We thus reach

\begin{equation} \label{eq:sigma_av2} \left\langle \dfrac{d\sigma}{d\Omega}\right\rangle = \langle (\delta b_j)^2 \rangle + \langle (\delta b_{j'})^2 \rangle + \langle b_j \rangle^2 + \langle b_{j'} \rangle ^2 + 2 \langle b_j \rangle \langle b_{j'} \rangle \cos ({\bf q} \cdot ({\bf r}_j - {\bf r}_{j'})). \end{equation}

We introduce the incoherent scattering cross section

\begin{equation} \label{eq:sigma_av3} \sigma_{inc,j} = 4 \pi \langle ( \delta b_j )^2 \rangle \end{equation}

and rewrite \eqref{eq:sigma_av2} to give

\begin{equation}\label{eq:nuclear_incoherent1} \left\langle \dfrac{d\sigma}{d\Omega}\right\rangle = \dfrac{\sigma_{{\rm inc},j} + \sigma_{{\rm inc},j'}}{4 \pi} + \left|\langle b_j\rangle \exp(i \mathbf{q}\cdot {\mathbf r}_j) + \langle b_{j'}\rangle \exp(i \mathbf{q}\cdot {\mathbf r}_{j'})\right|^2 . \end{equation}

Here we notice that the incoherent cross section, \(\sigma_\text{inc}\), represents a constant scattering of neutrons, i.e. in all directions, without interference between scattering from neighbour atoms. The average value \(\langle b_j\rangle\) represents the strength of the interfering scattering and is denoted the coherent scattering length. In general, the coherent scattering depends on the scattering vector \(\bf q\), and hence on the scattering angle. One defines coherent scattering cross section for a single nucleus \(j\) as \(\sigma_{\rm{coh},j}= 4 \pi \langle b_j\rangle^2 \).

Usually, the explicit average notation \(\langle b \rangle\) is dropped, and the symbol \(b\) almost exclusively means the average scattering length of a certain isotope or element. This is also the notation used in Table xx--CrossReference--tab:cross--xx.

Incoherent nuclear scattering from randomness

There are several sources of the incoherent scattering, described in general terms above. One source is the spin-dependent term, which is described in detail in , and which is the one given by the isotope tables. Below, we will deal with incoherent scattering caused by variations in the scattering length due to isotopic mixture or chemical randomness. From the point of view of unpolarized neutron scattering, all these mechanisms are very similar, as described above. The values of the incoherent scattering cross sections for the elements, found in Table xx--CrossReference--tab:cross--xx, deal with the combined effect from spin and isotopic mixture.

For a simple example, assume that a material consists of two isotopes with the abundances \(a_c=a\), and \(a_d=1-a\), the scattering lengths \(b_c\) and \(b_d\), respectively, and no nuclear spin. The average scattering length is

\begin{equation}\label{dummy104856507} \langle b \rangle = a b_c + (1-a) b_d ,\, \end{equation}

and the average incoherent cross section can be calculated by an average over the isotope abundances:

\begin{equation} \label{eq:sigma_mix} \dfrac{\sigma_{\rm inc}}{4\pi} = \langle (\delta b)^2 \rangle = a (b_c-\langle b \rangle)^2 + (1-a) (b_d-\langle b \rangle)^2 = a (1-a) (b_c - b_d)^2 . \end{equation}

This means that we see an incoherent scattering due to the isotope mixture, strongest at 50%-50% mixing ratio.

With a little effort, \eqref{eq:sigma_mix} can be generalized to more than two isotopes.

The magnetic scattering length

Unpaired electrons may introduce a magnetic moment localized on (some of) the atoms in the material. The details of this is elaborated in Elastic magnetic scattering, but let us for now assume that each atom has an effective spin, \({\bf s}_j\), that is zero for non-magnetic atoms. The magnetic dipole moment generated by the spin is \begin{equation} \label{eq:emoment} {\bf m}_j = g \mu_{\rm B} {\bf s}_j , \end{equation} where \(g=2.0023\) is the electronic magnetogyric ratio (the g-factor) and \(\mu_{\rm B} = e\hbar/(2m_{\rm e}) = 9.2741 \cdot 10^{-24}\)~J/T is known as the Bohr magneton.

As we discussed earlier, the neutron also has a magnetic moment, given by \begin{equation} {\bf \mu} = \gamma \mu_{\rm N} {\bf \sigma} , \end{equation}

where \(\gamma= - 1.91304\) is the neutron magnetogyric ratio and the nuclear magneton is given by \(\mu_{\rm N} = e \hbar / (2 m_{\rm p}) = 5.05078 \cdot 10^{-27}\)~J/T. \({\bf \sigma}\) represents the direction of the nuclear spin and has a length of unity. (For readers with a knowledge of quantum mechanics, \({\bf \sigma}\) is given by the three Pauli matrices.)

Each magnetic moment in the material gives rise to a magnetic dipole field, and during the scattering process, the neutron is affected by the forces that arises from variations of this field. These forces give rise to scattering in a rather similar way as the scattering of neutrons from nuclei that we discussed earlier. The detailed calculation of this scattering is lengthy and involves plenty of electromagnetism and quantum mechanics. For this reason, we present it elsewhere; in Quantum mechanics of magnetic diffraction.

The final result of the magnetic scattering, however, can be stated in three simple points:

• The scattering involves only \({\bf s}_{j,\perp} \), which is the component of \({\bf s}_j\) perpendicular to the scattering vector, \({\bf q}\).
• The magnetic scattering length decays for larger values of \(|{\bf q}|\) due to the smearing`` of the atomic spins across their respective orbitals.
• The magnetic scattering length depends on the relative orientation of the nuclear spin, \(\bf \sigma\), and the atomic spin, \({\bf s}_j\).

In brief, the magnetic scattering length for the individual atom, \(j\), can be written as

\begin{equation} b_{{\rm m},j} = \gamma r_0 {\bf \sigma} \cdot {\bf s}_{j,\perp} F_{\rm m}({\bf q}), \end{equation}

where \(r_0=e^2\mu_0/(4\pi m_{\rm e})=2.8179\)~fm is the classical electron radius.

The magnetic form factor, corresponding to point 2 above, is denoted by the symbol \(F_{\rm m}({\bf q})\) and is equivalent to the atomic form factor in X-ray scattering. It is given by

\begin{equation} F({\bf q}) = \int \exp(i {\bf q} \cdot {\bf r}) \rho_s({\bf r}) d^3{\bf r} \, , \end{equation}

where \(\rho_s({\bf r})\) is the normalised spin density on the unfilled orbitals. For small values of \(q\), below around 2~\AA , the magnetic form factor is close to unity, \(F(| {\bf q}| )=1\), and it falls off smoothly to zero for large scattering vectors.

In the following, we assume that the magnetic form factor is identical for all magnetic ions in the material under investigation, even though this may be too simple an approach, in particular for materials containing more than one magnetic element.

Experimental considerations

The magnitude of the magnetic scattering length is similar to the nuclear scattering lengths, since \(\gamma r_0 = 5.39\)~fm and \(s F(q) g/2\) is of the order unity. Hence, the magnetic and nuclear scattering cross sections have similar magnitudes. For \(S > 1\), e.g. in some transition metal salts, like Fe-oxides, or in most rare-earth compounds, the magnetic scattering can even completely dominate the diffraction patterns.

Correlation between nuclear and magnetic scattering

To describe the total scattering from a magnetic material, we must treat both the nuclear and the magnetic contributions to the scattering length. We therefore expand (\ref{eq:diffraction}) to reach. \begin{equation} \label{eq:diffraction_nandm} \left.\frac{d\sigma}{d\Omega}\right|_{\rm coh} = \biggr|\sum_j \left(b_j + b_{{\rm m},j}\right) \exp(i {\bf q} \cdot {\bf r}_j ) \biggr|^2 \, . \end{equation} Expanding the square, we obtain a double sum \begin{equation} \left.\frac{d\sigma}{d\Omega}\right|_{\rm coh} = \sum_{j,j'} (b_j + b_{{\rm m},j})(b_{j'} + b_{{\rm m},j'}) \exp(i {\bf q} \cdot ({\bf r}_j-{\bf r}_{j'})) \, . \end{equation} We now rearrange this to obtain four double sums: \begin{eqnarray} \label{eq:foursums} \left.\frac{d\sigma}{d\Omega}\right|_{\rm coh} &=& \sum_{j,j'} (b_j \exp(i {\bf q} \cdot {\bf r}_j)) (b_{j'}\exp(- i {\bf q} \cdot {\bf r}_{j'}))\\ \nonumber &+& \sum_{j,j'} (b_{{\rm m},j} \exp(i {\bf q} \cdot {\bf r}_j)) ( b_{j'}\exp(- i {\bf q} \cdot {\bf r}_{j'})) \\ \nonumber &+& \sum_{j,j'} (b_j \exp(i {\bf q}\cdot {\bf r}_j)) (b_{{\rm m},j'}\exp(- i {\bf q} \cdot {\bf r}_{j'})) \\ \nonumber &+& \sum_{j,j'} (b_{{\rm m},j} \exp(i {\bf q} \cdot {\bf r}_j)) ( b_{{\rm m},j'}\exp(- i {\bf q} \cdot {\bf r}_{j'})) \, . \end{eqnarray}

Let us for simplicity redefine the constituents of (\ref{eq:foursums}) as

\begin{eqnarray} N({\bf q}) &=& \sum_j b_j \exp(i {\bf q} \cdot {\bf r}_j) \nonumber \\ {\bf M}({\bf q}) &=& \gamma r_0 F_{\rm m}({\bf q}) \sum_j {\bf S}_{j,\perp} \exp(i {\bf q} \cdot {\bf r}_j) . \end{eqnarray}

Here, the symbol \(N({\bf q})\) is the Fourier transform of the nuclear scattering length, and \({\bf M}({\bf q})\) represents the Fourier transform of the magnetic scattering length except the dot product with the nuclear spin \({\bf \sigma}\).

With these definition, the cross section (\ref{eq:foursums}) becomes

\begin{equation} \label{eq:blumeminusone} \left.\frac{d\sigma}{d\Omega}\right|_{\rm coh} = |N({\bf q})|^2 + {\bf M}({\bf q}) \cdot {\bf M}^*({\bf q}) + 2 \Re \left\{ {\bf \sigma} \cdot {\bf M}({\bf q}) N^*({\bf q})\right\} . \end{equation}

To be able to continue this derivation, we have to choose an axis of quantization of the neutron spin. For convenience, let us take the \(z\)-direction. We define the neutron polarization along this direction as

\begin{equation} P_z = \langle \sigma_z \rangle = \frac{n^\uparrow- n^\downarrow}{n^\uparrow + n^\downarrow} , \end{equation}

where \(n^\uparrow\) represents the number of neutrons in the beam that has its spin up`` and similar for spin down``. (In quantum mechanics, the spin of a spin-\(1/2\) particle along any given direction can take only two values). The maximal value of \(P_z\) is unity. The beam can also be polarized in other directions, leading to the polarization vector \({\bf P}\), which has a maximal length on unity.

Most neutron scattering is performed with unpolarzed neutron beams. This means that for any direction, there will be as many spin up`` as spin down`` neutrons, meaning that \(\langle \sigma_z \rangle = 0\). This also holds for \(\langle \sigma_x \rangle\) and \(\langle \sigma_y \rangle\). When we now take the average cross section over the polarization direction, the term \({\bf \sigma} \cdot {\bf M}({\bf q}) N^*({\bf q})\) will be averaged to \(\langle {\bf \sigma} \rangle \cdot {\bf M}({\bf q}) N^*({\bf q})\), which vanishes, leaving only the \(|N({\bf q})|^2\) and \(|{\bf M}({\bf q})|^2\) terms non-zero.

We hereby see that for diffraction with unpolarized neutrons, the nuclear-magnetic interference term vanish, and therefore the scattering cross section is simply a sum of the nuclear and the magnetic term:

\begin{equation} \label{eq:nuclearmagnetic} \left.\frac{d\sigma}{d\Omega}\right|_{\rm coh} = |N({\bf q})|^2 + {\bf M}({\bf q}) \cdot {\bf M}^*({\bf q}) = \left.\frac{d\sigma}{d\Omega}\right|_{\rm nuc, coh} +\left.\frac{d\sigma}{d\Omega}\right|_{\rm magn, coh} \, . \end{equation}

It should already here be said that the expression (\ref{eq:blumeminusone}) is not entirely correct. In the (rare, but possible) case that both the magnetic structure has a chiral order, e.g. a spiral structure, and the neutron beam is polarized, an additional term will appear in the cross section : \begin{equation} {\bf P} \cdot \Im \left\{ {\bf M}({\bf q}) \times {\bf M}^*({\bf q}) \right\}. \end{equation}

This term will be elaborated in a future chapter on polarized neutron scattering.

Experimental considerations

Also magnetic scattering can be incoherent. In a magnetic system at sufficiently high temperatures, the spin directions are random, also known as a paramagnet. Such an unordered phase gives rise to uncorrelated directions of \({\bf b}_{{\rm m},j}\), and therefore incoherent scattering. This scattering does not correlate with the nuclear incoherent scattering, as will be shown in section \ref{sect:paramagnet}. Hence, also the incoherent cross section can be written as a sum of a nuclear and a magnetic contribution.

The total cross section for a system of particles

We have seen above that the total cross section can be written as a sum of the coherent and incoherent cross sections. In general, each of these cross sections can have an elastic and an inelastic part, giving rise to four terms:

\begin{equation}\label{dummy260518738} \frac{d^2\sigma}{d\Omega dE_{\rm f}} = \displaystyle\sum_j \frac{d\sigma_j}{d\Omega}\biggr|_{\rm inc} \delta(\hbar\omega) + \frac{d\sigma}{d\Omega}\biggr|_{\rm coh} \delta(\hbar\omega) + \displaystyle\sum_j \frac{d^2\sigma_j}{d\Omega dE_{\rm f}}\biggr|_{\rm inc} + \frac{d^2\sigma}{d\Omega dE_{\rm f}}\biggr|_{\rm coh} . \end{equation}

where each of the four terms will contain both a nuclear and a magnetic contribution. We will in the remainder of these notes concentrate upon the two coherent scattering processes, unless explicitly noticed.

Experimental considerations

The distinction between coherent and incoherent scattering is very important. In most types of experiment you will aim to minimize the incoherent cross section, which creates a uniform background, and maximize the coherent cross section, which generates the features you intend to study. A typical strong source of incoherent scattering is hydrogen, \(^1\)H, where the incoherence is due to a strong spin dependence of the interaction between the neutron and the proton.

Inelastic incoherent scattering can, however, be used to study dynamic processes; mostly the motion of hydrogen. This type of scattering is not discussed further in this version of the notes.

Beam attenuation due to scattering and absorption

The cross sections for scattering and absorption are additive due to the rule of addition of probabilities (see Problem: Attenuation of the neutron beam), giving the total volume specific cross section: \begin{equation} \Sigma_{\rm t} = \Sigma_{\rm s} + \Sigma_{\rm a}. \end{equation}

Since the number of neutrons scattered or absorbed is necessarily limited by the number of incoming neutrons, the total cross section cannot be truly proportional to the number of nuclei, at least not for large, strongly scattering/absorbing systems. Hence, (\ref{eq:Sigma_def}) should be understood only as what is called the em thin sample approximation or the Born approximation. This equation is valid only when the total scattering cross section of a given sample is much smaller than its area perpendicular to the beam. Note that the total cross section of a sample cannot exceed its area. This would lead to the number of scattered neutrons exceeding the number of incoming neutrons, which is not possible.

For a thick sample, we must consider successive thin slices of thickness \(dz\), each attenuating the incident beam (which we take to travel in the positive \(z\) direction):

\begin{equation} {\rm \; no.\; of\; neutrons\; scattered\; or\; absorbed\; per\; sec.\; from\;} dz = \Psi(z) \Sigma_{\rm t} A dz , \end{equation} where \(A\) is the area of a sample slice perpendicular to the beam. We assume that \(A\) and \(\Sigma_{\rm t}\) are constants and that the scattering and absorption cross section is uniform within the sample. The flux of the incident beam in the neutron flight direction is then attenuated inside the sample according to

\begin{equation} \label{eq:attenuation} \Psi(z) = \Psi(0) \exp(-\mu_{\rm t} z) \, , \end{equation}

where we have defined the total attenuation coefficient \begin{equation} \mu = \mu_{\rm t} = \Sigma_{\rm t} . \end{equation}

The derivation is simple and is left as an exercise to the reader, see Problem: Attenuation of the neutron beam.

When the attenuation coefficient varies along the neutron path, (\ref{eq:attenuation}) is generalized to \begin{equation} \label{eq:attenuation2} \Psi(z) = \Psi(0) \exp\left(-\int_0^z \mu(z') dz' \right) \, . \end{equation}

This equation is essential in the use of neutron transmission for real-space imaging of samples, in analogy to medical X-ray images. This application of neutrons will be elaborated more in Imaging.

←   Previous page: Introduction to neutron scattering
→   Exercises: Exercises in Basics of neutron scattering
→   Next page: Quantum treatment of elastic neutron scattering