The neutron cross sections

We fist introduce the terms by which we describe the scattering of a neutron beam. In particular, we describe the interaction of a neutron beam with materials by introducing the central concept of cross sections.

Neutron flux

We define the flux of a neutron beam as the neutron rate per area

\begin{equation}\label{dummy378179674} \Psi = \dfrac{ {\rm number\; of\; neutrons\; impinging\; on\; a\; surface\; per\; second}} { {\rm surface\; area\; perpendicular\; to\; the\; neutron\; beam\; direction}} , \end{equation}

usually given in the unit n/(cm\(^2\)s).

Experimental considerations

At most neutron scattering experiments, the incoming flux at the sample position lies in the range \(10^4\) to \(10^9\) n/(cm\(^2\)s). At ESS, however, some instruments will reach a flux of \(10^{10}\) n/(cm\(^2\)s).

The scattering cross section

The neutron scattering cross section, \(\sigma\), of a system is defined by the system's ability to scatter neutrons:

\begin{equation}\label{eq:sigma_def} \sigma = \dfrac{1}{\Psi} \cdot { {\rm number\; of\; neutrons\; scattered\; per\; second}} , \end{equation}

which has units of area. The scattering intensity is divided by the neutron flux to ensure that \(\sigma\) is an intrinsic property, independent on the neutron flux at the particular experimental set-up.

For a single nucleus, \(\sigma\) can now be seen as the effective area of the nucleus perpendicular to the neutron beam, as will be elaborated in the problem the cross section. The scattering cross section used here is the total cross section, which depends on the system (sample) volume, \(V\). For thin samples, \(\sigma\) can be described by the volume specific cross section, \(\Sigma\), through

\begin{equation}\label{eq:Sigma_def} \sigma = V \Sigma .\, \end{equation}

For thicker samples, beam attenuation must be taken into account; see the section Beam attenuation due to scattering.

The differential scattering cross section

The angular dependence of the scattered neutrons is a most important aspect of all neutron scattering. To describe this dependence, we define the differential scattering cross section as the intensity of neutrons scattered into a particular solid angle, \(d\Omega\). We denote the wave vector of the incoming neutron by \(k_i\) and that of the outgoing neutron by \(k_f\), where the indices "i" and "f" denote initial and final, respectively. This is illustrated in Figure xx--CrossReference--fig:Fig2dot1v3.png--xx and is quantified as:

Figure 1: An illustration of the scattering geometry. The incoming neutrons, labeled \(k_i\), scatter at the center of the sphere with the scattering angle \(2\theta\) and azumital angle \(\phi\). The neutrons scattered into the solid angle element \(d\Omega\) (or detector area \(dA\) ar labeled with \(k_f\).

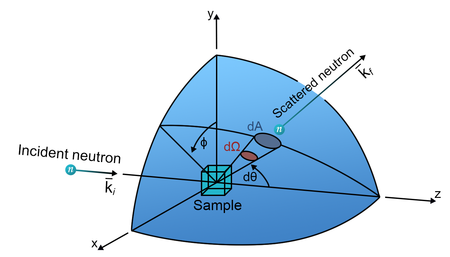
\begin{equation}\label{eq:dscs} \frac{d\sigma}{d\Omega} = \frac{1}{\Psi} \frac{{\rm \; number\; of\; neutrons\; scattered \; into\; solid\; angle\;} d\Omega{\rm \; per\; second}}{d\Omega} . \end{equation}

The total number of scattered neutrons is the integral of neutrons per solid angle over all of the \(4\pi\) solid angle, hence

\begin{equation}\label{eq:dscs_int} \sigma = \displaystyle\int \dfrac{d\sigma}{d\Omega} d\Omega . \end{equation}

The partial differential scattering cross section

In some scattering processes, the neutron delivers energy to or absorbs energy from the scattering system. This type of scattering we denote inelastic scattering. We define the neutron energy transfer by

\begin{equation}\label{eq:inelastic_basic} \hbar \omega = E_{\rm i} - E_{\rm f}, \end{equation}

which can also be written as

\begin{equation}\label{eq:inelastic_basic2} \hbar \omega = \dfrac{\hbar^2(k_{\rm i}^2-k_{\rm f}^2)}{2 m_{\rm n}}. \end{equation}

Note that the energy change is defined with the opposite sign of most definitions of changing properties, so that neutron energy loss gives a positive value of \(\hbar \omega\), while neutron energy gain gives negative values.

In inelastic scattering processes, energy is transfered to - or taken from - the sample. Energy conservation gives that the energy change, \(\Delta E\), of the sample is given by

\begin{equation}\label{dummy1737456334} \Delta{}E = \hbar \omega . \, \end{equation}

For describing inelastic scattering, one needs to take into account the energy dependence of the scattered neutrons. This is described by the partial differential scattering cross section:

\begin{equation}\label{eq:pdscs} \dfrac{d^2\sigma}{d\Omega dE_{\rm f}} = \dfrac{1}{\Psi} \dfrac{ { {\rm number\; of\; neutrons\; scattered\; per\; sec.\; into\;}} d\Omega\; { {\rm with\; energies\;}} [ E_{\rm f};E_{\rm f}+dE_{\rm f} ] } {d\Omega dE_{\rm f}} . \end{equation}

Integrating over the all final energies, \(E_{\rm f}\), we reach the differential cross section described earlier:

\begin{equation}\label{dummy222151533} \dfrac{d\sigma}{d\Omega} = \displaystyle\int \dfrac{d^2\sigma}{d\Omega dE_{\rm f}} dE_{\rm f}. \end{equation}

Following equation \eqref{eq:dscs_int}, the total cross section is found by a double integration:

\begin{equation}\label{dummy350986584} \sigma = \displaystyle\iint \dfrac{d^2\sigma}{d\Omega dE_{\rm f}} d\Omega dE_{\rm f}. \end{equation}

For a closer description of inelastic scattering, a quantum mechanical treatment of the scattering process is required, as initiated in the section Quantum mechanics of scattering and described in detail in the part on dynamics of materials.

The absorption cross section

Neutron absorption takes place as a result of neutron-induced nuclear processes, which destroy the neutrons, emitting secondary radiation (\(\alpha\), \(\beta\), or \(\gamma\)) as a result. In most cases, the absorption cross section, \(\sigma_{\rm a}\), of thermal neutrons is inversely proportional to the neutron velocity. In other words, the absorption is proportional to the neutron wavelength: \(\sigma_{\rm a} \propto \lambda\).

The neutron absorption cross sections are measured and tabelized for all but the rarest isotopes, see e.g. the Neutron Data Booklet, or the NIST home page. Traditionally, the absorption cross section of isotope \(j\) is given as \(\sigma_{\text{a,j,th}}\) per nucleus in units of "barns" (1 barn \(=10^{-28}\) m\(^{2}\)) and is listed at the standard "thermal" velocity \(v_\text{th} = 2200\) ms\(^{-1}\) (\(\lambda_\text{th} = 1.7982\) Å, see also the neutron unit conversion table on the Introduction to neutron scattering page). The actual absorption cross section is then given by

Table 1: Neutron cross sections and scattering lengths for the first 32 elements (isotopic average using the natural abundancies). In addition, data for selected isotopes and for some heavier elements are presented. Data taken from . * It should be noted that the important incoherent cross section for H varies with neutron wavelength. The value listed is valid for \(\lambda > 1.798\) Å

\begin{equation}\label{dummy2114890051} \sigma_{\rm a,j} = \sigma_{\text{a,j,th}} \dfrac{v_\text{th}}{v} = \sigma_{\text{a,j,th}} \dfrac{\lambda}{\lambda_\text{th}}. \end{equation}

Also for absorption, the volume specific cross section is defined as

\begin{equation}\label{dummy21148900512} \sigma_{\rm a,j} = V \Sigma_{\rm a,j}. \end{equation}

In a general material, many nuclei contribute to the total absorption. As in equation \eqref{eq:attenuation}, the resulting attenuation coefficient is

\begin{equation}\label{dummy74943618} \Sigma_{\rm a} = \sum_j \dfrac{N_j \sigma_{ {\rm a},j}}{ V} = \sum_j n_j \sigma_{ {\rm a},j}. \end{equation}

In this sum, \(N_j\) represents the number of nuclei of isotope, \(j\) in the sample volume \(V\), and \(n_j=N_j/V\) is their respective atomic density.

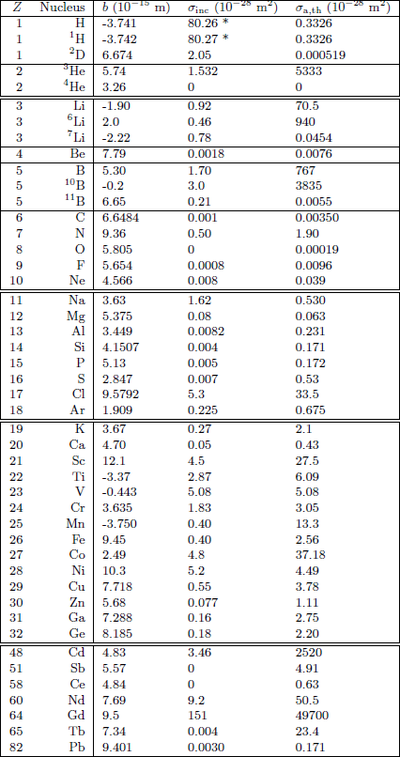
An abbreviated list of absorption and scattering cross sections for selected isotopes/elements is given in Table xx--CrossReference--tab:cross--xx.