Problem: SANS and SAXS from spherical surfactant micelles

Figure 1: (left) Molecular structure of the surfactant Sodium Dodecyl Sulphate (SDS). (right) Illustration of the cross-section of a spherical micelle.

The experimental setup of a Small-angle X-ray scattering (SAXS) instrument is in principle very similar to that of the SANS instrument. The main difference between the two methods is that in SANS, the incoming neutrons are scattered by the nuclei of the studied sample, whereas in SAXS the incoming photons are scattered by the electrons of the studied sample.

The scattering length of an electron, \(b_{\rm e}\) is given by the classical electron radius (also known as the Compton radius or the Thompson scattering length). It is calculated from \(b_{\rm e}= e^2/(4 \pi \varepsilon_0 m_{\rm e} c^2)= 2.82\) fm, where \(\varepsilon_0\) is the vacuum permittivity, \(e\) and \(m_{\rm e}\) are the charge and mass of the electron and \(c\) is the speed of light. Thus the scattering length of an atom with atomic number \(n\) is simply \(n b_{\rm e}\).

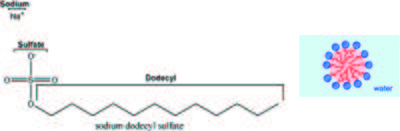
The anionic surfactant Sodium Dodecyl Sulphate (SDS) (see Figure xx--CrossReference--fig:sans_SDS_micelle--xx, left) is one of the main active components in ordinary dishwasher detergent. When dissolved in water, the SDS molecules self-organize into small spherical micelles, with the hydrophobic alkyl chains in the core of the micelles and the hydrophilic sodium sulphate head-groups surrounding the micelles (see Figure xx--CrossReference--fig:sans_SDS_micelle--xx, right). Assume that the aggregation number of the micelles, i.e. the average number of surfactant molecules per micelle, is 55 and that the micelles are perfectly monodisperse.

The partial specific mass density of SDS in water is 1.03 g/cm\(^3\). The maximal extension, \(l_{\rm max}\), and partial specific molecular volume, \(\nu\), of alkyl chains with \(n\) carbon atoms can be estimated from the so-called Tanford's formulas:

\( \begin{align*} l_\text{max} &= (1.54+1.265 \times n) {\rm Å} , \\ \nu &= (27.4+26.9 \times n) {\rm Å}^3. \end{align*} \)

Question 1

A combined SANS and SAXS experiment on SDS micelles in deuterated water (D\(_2\)O) is being planned (see the Complementarity of neutrons and X-rays section on the SANS page). Use the above information to calculate and sketch the excess scattering length density profiles, \(\rho(r)\) of the micelles in water for neutrons and for X-rays).

Hint

Figure 2: (a) Excess scattering length density profiles corresponding to a simple model of the TAC8 micelles assuming no hydration of the hydrophilic shell. The continuous line is for neutrons, and the broken line is for X-rays. (b) Cross-section of the prolate ellipsoidal TAC8 micelles. From Ref. .

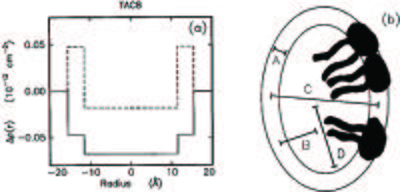
See Figure xx--CrossReference--fig:sans_rho--xx for an example of an excess scattering length density profile from another surfactant micelle system.

Question 2

Calculate and plot the expected SAXS and SANS scattering intensity curves, i.e. the particle form factor in a \(q\)-range from 0.001 Å\(^{-1}\) to 0.5 Å\(^{-1}\).

Question 3

Estimate how a spread of the wavelength of the incoming beam, \(\Delta \lambda / \lambda\) of 10 % FWHM will affect the SAXS and SANS intensity curves.

Question 4

In practice the micelles are polydisperse and can be described by a Gauss distribution with a reduced standard deviation \(\sigma(R)/\overline{R}=20\) %. Discuss how this polydispersity affects the SAXS and SANS intensity curves, respectively.