Problem: Bragg scattering from Bravais lattices
We will here investigate the effect of the nuclear structure factor in the total diffraction cross section for Bravais lattices. However, as we shall see, some Bravais lattices can with advantage be described as a lattice with a basis.
Question 1
For a simple cubic lattice, atom distance \(a\), the reciprocal lattice points are also simple cubic, with point distance \(\tau_{(001)} = 2 \pi / a\). Calculate the squared structure factor \(|F_{\rm N}({\boldsymbol\tau}_{hkl})|^2\) in units of the nuclear scattering length \(b\). Which reflections are allowed (non-zero structure factors)? Do the allowed reflections have different structure factors?
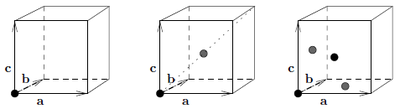
The simple cubic structure only has basisvector \({\mathbf d}=(0,0,0)\) in the cartesian coordinate system defined in Figure xx--CrossReference--fig:Sc_bcc_fcc--xx by \(\{ {\mathbf a},{\mathbf b},{\mathbf c} \}\). In general For Bragg scattering \({\mathbf q}={ \boldsymbol\tau}= h{\mathbf a}^* + k{\mathbf b}^* + l{\mathbf c}^* \). Hence e.g. \({ \boldsymbol\tau}_{(001)}=0\cdot{\mathbf a}^* + 0\cdot{\mathbf b}^* + 1\cdot{\mathbf c}^*={\mathbf c}^*\).
\begin{align} |F^{sc}_N({\boldsymbol\tau}_{hkl})|^2 &= \left| \displaystyle\sum_{ {\mathbf d}}b_{\mathbf d} e^{i \boldsymbol\tau_{hkl}\cdot {\mathbf d}} \right|^2\label{dummyafksjhfkjash1}\\ &= \left| b e^{i \frac{2\pi}{a}(h\cdot 0 + k\cdot 0 + l\cdot 0) } \right|^2\label{dummyafksjhfkjash2}\\ &= |b|^2 \label{dummyafksjhfkjash3} \end{align}
Since \({\mathbf q} \cdot {\mathbf d} = 0\) for any \(q\) here, hence giving \(|F_N|^2=|b|^2\) all reflections are allowed.
Question 2
A body centered cubic (bcc) lattice can be described as a simple cubic lattice (side length \(a\)) with a second atom placed in the centre of the cube. The metallic elements Cr and Fe are two examples. Calculate the distance between nearest lattice sites.
The bulk centered cubic structure has atoms at sites \({\mathbf d} \in \{ (0,0,0), a(\frac{1}{2},\frac{1}{2},\frac{1}{2})\}\) in the cartesian coordinate system defined in Figure xx--CrossReference--fig:Sc_bcc_fcc--xx by \(\{ {\mathbf a},{\mathbf b},{\mathbf c} \}\). The nearest neighbor distance is
\begin{equation}\label{dummyafksjhfkjash} d = \sqrt{\left( \dfrac{a\sqrt{2}}{2} \right)^2 + \left( \dfrac{a}{2} \right)^2 } = \dfrac{\sqrt{3}a}{2} \end{equation}
Calculate the expression for the nuclear structure factor of a bcc structure using \(b = 1\).
The structure factor is
\begin{align} |F_N^{bcc}({\mathbf \tau}_{(hkl)})|^2 &= \left| b \left( 1+ e^{i\frac{2\pi}{a}(h, k, l)\cdot (\frac{a}{2},\frac{a}{2},\frac{a}{2})} \right)\right|^2\label{dummyafksjhfkjas1h}\\ &= \left| b \left( 1+ e^{i\pi(h + k + l)}\right)\right|^2\label{dummyafksjhfkjashs} \end{align}
Which reflections \((h, k, l)\) are allowed? Do they have different structure factors?
Using \(b=1\) we get \(|F_N({\boldsymbol \tau}_{(hkl)})|^2 = |2b|^2 = 4\) for \(h+k+l\) even and \(|F_N({\boldsymbol \tau}_{(hkl)})|^2 = 0\) (disallowed) for \(h+k+l\) odd. All allowed reflections have the same structure factor and constitute an \(fcc\) lattice.
The structure factors you have calculated using \(b = 1\) are also called the geometrical structure factors. Can you think of a reason why?
The geometrical structure factor only has to do with the relative positions of the atoms.
Question 3
A face centered cubic (fcc) lattice (side length \(a\)) has atoms in the cube corners and at the centre of the cube faces. One example of an fcc system is Al. Calculate the distance between nearest neighbour lattice sites.
The face centered cubic structure has atoms at sites \({\mathbf d} \in \{ (0,0,0), a(\frac{1}{2},\frac{1}{2},0),a(0,\frac{1}{2},\frac{1}{2}), a(\frac{1}{2},0,\frac{1}{2})\}\) in the cartesian coordinate system defined in Figure xx--CrossReference--fig:Sc_bcc_fcc--xx by \(\{ {\mathbf a},{\mathbf b},{\mathbf c} \}\). The nearest neighbor distance is
\begin{equation}\label{dummy236186318} d = \sqrt{ \left( \dfrac{a}{2} \right)^2 + \left( \dfrac{a}{2} \right)^2 } = \dfrac{a}{\sqrt{2}} \end{equation}
Calculate the expression for the geometrical structure factor of the fcc structure.
The structure factor is
\begin{align}\label{dummy31763912769} |F_N^{fcc}({\mathbf \tau}_{(hkl)})|^2 &= \left| b \left( 1+ e^{i\frac{2\pi}{a}(h, k, l)\cdot (\frac{a}{2},\frac{a}{2},0)}+e^{i\frac{2\pi}{a}(h, k, l)\cdot (0,\frac{a}{2},\frac{a}{2})}+e^{i\frac{2\pi}{a}(h, k, l)\cdot (\frac{a}{2},0,\frac{a}{2})} \right)\right|^2\\ &= \left| b \left( 1 + e^{i\pi(h + k)} + e^{i\pi(k + l)} + e^{i\pi(h + l)}\right)\right|^2 \end{align}
Which reflections are allowed? Do they have different structure factors?
The structure factor is \(|F_N({\mathbf \tau}_{(hkl)})|^2 = |4b|^2\) for all \(h,k,l\) even or odd. Else disallowed.The allowed positions constitute a \(bcc\) lattice.
Question 4
How many lattice sites (atoms) are present in the unit cell of the simple cubic, the bcc, and the fcc lattices, respectively?
In the simple cubic crystal there is \(\frac{1}{8}\cdot8 = 1\) atom.
In the bulk centered cubic crystal there are \(\frac{1}{8}\cdot8 + 1 = 2\) atoms.
In the face centered cubic crystal there are \(\frac{1}{8}\cdot8 + \frac{1}{2}*6 = 4\) atoms.
Question 5
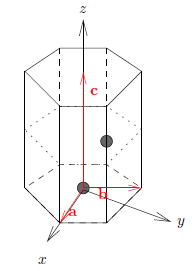
The hexagonal lattice is described by the lattice vectors \({\bf a} = a(1, 0,0)\), \({\bf b} = a(-1/2, \sqrt{3}/2, 0)\), and \({\bf c} = c(0, 0, 1)\) in orthogonal coordinates. Calculate the expression for the corresponding reciprocal lattice vectors.
In orthogonal coordinates the hexagonal lattice vectors can be written
\( \begin{align} {\mathbf a}_c &= a (1,0,0)\\ {\mathbf b}_c &= a \left( -\dfrac{1}{2},\dfrac{\sqrt{3}}{2},0 \right)\\ {\mathbf c}_c &= c(0,0,1)\\ \end{align}\)
Since \(V_0= {\mathbf a}\cdot {\mathbf b}\times{\mathbf c}= \frac{\sqrt{3}}{2}a^2c \), the reciprocal lattice vectors in the cartesian coordinate system are
\( \begin{align} {\mathbf a}_c^* &= \dfrac{2\pi}{V_0}{\mathbf b}\times {\mathbf c} = \dfrac{2\pi}{a} \left( 1,\dfrac{1}{\sqrt{3}},0 \right)\\ {\mathbf b}_c^* &= \dfrac{2\pi}{V_0}{\mathbf c}\times {\mathbf a} = \dfrac{2\pi}{a} \left( 0,\dfrac{2}{\sqrt{3}},0 \right)\\ {\mathbf c}_c^* &= \dfrac{2\pi}{V_0}{\mathbf a}\times {\mathbf b} = \dfrac{2\pi}{c}(0,0,1)\\ \end{align}\)
Question 6
The hexagonal closed-packed (hcp) lattice can be described as a hexagonal unit cell with a two-atom basis, where \({\bf d}_1 = (0,0,0)\) and \({\bf d}_2 = (a/2, a/(2 \sqrt{3}), c/2)\) in cartesian coordinates. Calculate the ratio \(c/a\), knowing that the distance between an atom and all 12 nearest neighbours must be equal.
The hcp structure can be described by a hexagonal unit cell with a two-atom basis. In cartesian coordinates the atom positions are
\begin{equation} {\mathbf d}_1 = (0,0,0) \qquad {\mathbf d}_2 = \left( \dfrac{a}{2},\dfrac{a}{2\sqrt{3}},\dfrac{c}{2} \right) \end{equation}
The nearest neighbor distance is $a$ for all atoms, hence
\begin{align} a &= |{\mathbf d}_2 - {\mathbf d}_1| = \sqrt{\left( \dfrac{a}{2} \right)^2 + \left( \dfrac{a}{2\sqrt{3}} \right)^2 + \left( \dfrac{c}{2} \right)^2} \Leftrightarrow \\ \dfrac{c}{a} &= 2 \sqrt{\dfrac{2}{3}} \approx 1.633 \end{align}
In the hexagonal crystal coordinates, the relative atom coordinates may be given as \((0,0,0)\) and \((2/3, 1/3, 1/2)\), i.e. in units of the three real-space lattice vectors. Explain how the value \((2/3, 1/3, 1/2)\) appears.
In hexagonal crystal coordinates the lattice vectors are
\begin{equation} {\mathbf a}_h = a(1,0,0), \quad {\mathbf b}_h = a(0,1,0), \quad {\mathbf c}_h = c(0,0,1) \end{equation}
Then the position of the basisatoms are
\begin{equation} {\mathbf d}_1 = (0,0,0)_c = (0,0,0)_h \qquad {\mathbf d}_2 = \left( \dfrac{a}{2},\dfrac{a}{2\sqrt{3}},\dfrac{c}{2} \right)_c = \dfrac{2}{3}{\mathbf a}_h + \dfrac{1}{3}{\mathbf b}_h +\dfrac{1}{2}{\mathbf c}_h = \left( \dfrac{2}{3},\dfrac{1}{3},\dfrac{1}{2} \right)_h \end{equation}
Question 7
Calculate the expression for the structure factor of the hcp lattice using \(b = 1\) and the atom positions in the hexagonal cell. Use the expression to calculate the geometrical structure factors for \((hkl) = (100)\), \((101)\), \((102)\), \((103)\), \((001)\), \((002)\), \((110)\), \((111)\) and \((112)\). Explain the regularities in the structure factors.
In the hexagonal crystal coordinates the basisatoms are at
\begin{align} {\mathbf d}_1 &= (0,0,0)\\ {\mathbf d}_2 &= \left( \dfrac{2}{3},\dfrac{1}{3},\dfrac{1}{2} \right)= \dfrac{2}{3}{\mathbf a} + \dfrac{1}{3}{\mathbf b} + \dfrac{1}{2}{\mathbf c} \end{align}
A general position in the realspace crystal is \({\mathbf d} = n_a{\mathbf a}+n_b{\mathbf b}+n_c{\mathbf c} \). The reciprocal lattice vectors in hexagonal crystal coordinates are
\begin{align} {\mathbf a}^* &= \dfrac{2\pi}{a}{\mathbf b}\times {\mathbf c} = \dfrac{2\pi}{a} (1,0,0)\\ {\mathbf b}^* &= \dfrac{2\pi}{a}{\mathbf c}\times {\mathbf a} = \dfrac{2\pi}{a} (0,1,0)\\ {\mathbf c}^* &= \dfrac{2\pi}{c}{\mathbf a}\times {\mathbf b} = \dfrac{2\pi}{c}(0,0,1)\\ \end{align}
The scattering vectors can be written \({\boldsymbol \tau}\) = \(h {\mathbf a}^* + h {\mathbf b}^* + k {\mathbf c}^* \equiv (h k l)\), hence the structure factors are
\begin{equation} \left|F(hkl)\right|^2 = \left| \displaystyle\sum_{ {\mathbf d}}b_{\mathbf d} e^{i {\boldsymbol \tau}_{\rm (hkl)}\cdot {\mathbf d}} \right|^2 = \left| \displaystyle\sum_{n_an_bn_c}b_{n} e^{i 2\pi (n_a h + n_bk + n_c l)} \right|^2 = \left| 1 + e^{i 2\pi (\frac{2}{3} h + \frac{1}{3}k + \frac{1}{2} l)} \right|^2 \end{equation}
And specifically
\begin{align} \left|F(100)\right|^2 &= \left| 1 + e^{i (\frac{4\pi}{3})} \right|^2 = \left( 1+\cos\left(\dfrac{4\pi}{3}\right)+ i\sin\left(\dfrac{4\pi}{3}\right)\right)\left( 1+\cos\left(\dfrac{4\pi}{3}\right)- i\sin\left(\dfrac{4\pi}{3}\right)\right) = (1-0.5)^2 + 0.75 = 1\\ \left|F(101)\right|^2 &= \left| 1 + e^{i 2\pi(\frac{7}{6})} \right|^2 = \left( 1+\cos\left(\dfrac{7\pi}{3}\right)+ i\sin\left(\dfrac{7\pi}{3}\right)\right)\left( 1+\cos\left(\dfrac{7\pi}{3}\right)- i\sin\left(\dfrac{7\pi}{3}\right)\right) = (1+0.5)^2 + 0.75 = 3\\ \left|F(102)\right|^2 &= \left| 1 + e^{i 2\pi(\frac{5}{3})} \right|^2 = \left( 1+\cos\left(\dfrac{10\pi}{3}\right)+ i\sin\left(\dfrac{10\pi}{3}\right)\right)\left( 1+\cos\left(\dfrac{10\pi}{3}\right)- i\sin\left(\dfrac{10\pi}{3}\right)\right) = (1-0.5)^2 + 0.75 = 1\\ \left|F(103)\right|^2 &= \left| 1 + e^{i 2\pi(\frac{13}{6})} \right|^2 = \left( 1+\cos\left(\dfrac{13\pi}{3}\right)+ i\sin\left(\dfrac{13\pi}{3}\right)\right)\left( 1+\cos\left(\dfrac{13\pi}{3}\right)- i\sin\left(\dfrac{13\pi}{3}\right)\right) = (1+0.5)^2 + 0.75 = 3\\ \left|F(001)\right|^2 &= \left| 1 + e^{i \pi} \right|^2 = 0\\ \left|F(002)\right|^2 &= \left| 1 + e^{i 2\pi} \right|^2 = 4\\ \left|F(110)\right|^2 &= \left| 1 + e^{i 2\pi(\frac{2}{3}+\frac{1}{3})} \right|^2 = 4\\ \left|F(111)\right|^2 &= \left| 1 + e^{i 2\pi(\frac{2}{3}+\frac{1}{3}+\frac{1}{2})} \right|^2 = 0\\ \left|F(112)\right|^2 &= \left| 1 + e^{i 2\pi(\frac{2}{3}+\frac{1}{3}+1)} \right|^2 = 4\\ \end{align}
Hence for \(h=k\): \(F^2=0\) for \(l\) odd and \(F^2=4\) for \(l\) even . For \(k+k\) odd: \(F^2=3\) for \(l\) odd and \(F^2=1\) for \(l\) even.