Problem:The neutron guide system
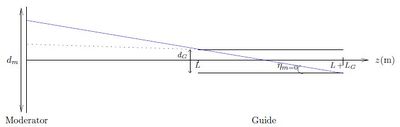
Consider a 20 m long Ni (\(m=1\)) guide with a constant square cross section \(50 \times 50\) mm\(^2\), illuminated by a moderator of area \(d^2 = 150 \times 150\) mm\(^2\) at a distance, \(L\). We can assume that \(L \gg d\).
Question 1
Calculate the critical scattering angle at the guide for 4 Å and 20 Å neutrons.
Assume the critical scattering angle \( \theta_c \) is small.
The critical scattering angle is found from
- \( Q_c = 2k \sin{\theta_c(\lambda)} \approx 4\pi \dfrac{\theta_c(\lambda)}{\lambda} \quad\Rightarrow\quad \theta_c(\lambda) \approx \dfrac{Q_c \lambda}{4\pi} .\)
For Ni and \(m=1\) the critical scattering vector is \(Q_c=0.0219\) Å\(^{-1}\) giving \(\theta_c( 4\) Å \() \approx 0.007 \text{rad} = 0.4^\circ\) and \(\theta_c(20\) Å\()\approx 0.035~\text{rad} = 2^\circ\). Only neutrons with smaller angles are reflected in the guide.
Question 2
What is the maximal (horizontal or vertical) divergence of neutrons that passes through the guide without being reflected? Compare this to the previous question.
The maximal vertical (or horizontal) divergence of neutrons passing through the guide without being reflected (equivalent to guide with \(m=0\))
- \( \def\AA{\unicode[serif]{xC5}} \eta_{m=0} = \tan^{-1} \dfrac{d_G}{L_G} = \tan^{-1} \dfrac{0.05}{20} = 0.14^\circ < \theta_c(4 \rm{\AA}) \wedge \theta_c(20\rm{\AA}) ,\)
where the notation refers to Figure xx--CrossReference--fig:Guide--xx.
Question 3
A guide is "underilluminated" when the moderator size, not the guide reflectivity, limits the divergence of the transmitted neutrons in any direction. How close must the guide be to the moderator in order not to be underilluminated at 4 Å and 20 Å wavelengths?
Calculate the maximum divergence of a neutron ray which illuminates the entire guide cross-section \(d_G=0.05\) m.
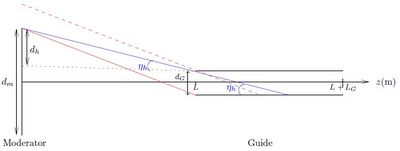
The notation of the following refers to Figure xx--CrossReference--fig:Guideillumination--xx. The maximum divergence of a neutron which illuminates the entire guide cross-section (height/width \(d_G=0.05\) m)
- \( \eta_h = \tan^{-1} \dfrac{d_h}{L} = \tan^{-1} \dfrac{d_m-d_G}{2L} \quad\Leftrightarrow\quad L=\dfrac{d_m -d_G}{2 \tan{\eta_h}} .\)
The guide is not underilluminated when \(\eta_h > \theta_c\), so
- \( L(\lambda=4 \rm{\AA}) < \dfrac{0.1\text{m}}{2\tan{\theta(4\rm{\AA})}} = 7.2 \text{m} , \)
- \( L(\lambda=20 \rm{\AA}) < \dfrac{0.1\text{m}}{2\tan{\theta(20\rm{\AA})}} = 1.4 \text{m} .\)
So if the guide is placed at 1.4 m or closer to the moderator it is not underilluminated for \(\lambda<20\) Å.
Question 4
Compare the neutron flux at \(\lambda = 4\) Å at the end of the guide (placed at \(L=1.5\) m) with the flux in the situation where the guide is removed and replaced with a beam port placed at 21.5 m from the moderator.
The flux at the detector is proportional to the area of the moderator which the neutrons arriving at the detector span. You can assume the distance to each point in the guide/beamport opening from each point on the moderator to be the same.
The guide entry is placed at \(L=1.5\) m so it is not underilluminated by 4 Å neutrons, and neutrons with divergence less than \(\theta_c\) are reflected and propagated to the end of the guide. However, if the guide is replaced by a beamport only those with divergence less than \(\eta_{m=0}\) will pass to point \(L+L_G\). The relative flux from guide compared to beamport at \(\lambda=4\) Å is therefore
- \( \dfrac{\Psi_{\text{Guide}}}{\Psi_{\text{Beamport}}} = \dfrac{d\Omega_\text{Guide}}{d\Omega_\text{Beam port}} \approx \dfrac{\theta_c^2(4\rm{\AA})}{\eta_{m=0}^2}=\dfrac{0.4^2}{0.14^2}=8 .\)
Another way of realising this is by imagining a small pinhole at the guide entrance. The neutrons passing through this hole to the end of the guide would have come from an area of size \((\theta_c(4\) Å\()\cdot1.5 \rm{m})^2 = 0.36 \rm{m}^2\) on the moderator in case of the guide with \(m=1\). Similarly in case of a beamport instead of the guide (\(m=0\)), \((\eta_{m=0}\cdot1.5 \rm{m})^2 = 0.044 \rm{m}^2\).
Integrating over the area of the guide entrance (moving the pinhole over the guideopening) would in each case just add a factor of the guide area \(A_G\) if we assume that the distance to each point in the guide opening from each point on the moderator is the same. Hence the relative flux would be
- \( \dfrac{\Psi_{\text{Guide}}}{\Psi_{\text{Beamport}}}= \dfrac{0.36\, A_G}{0.044\, A_G}=8 .\)
Question 5
Can you imagine why guides are often not used for instruments using thermal or hot neutrons?
Compare the critical angle in an \(m=1\) Ni guide for thermal neutrons with \(\lambda = 2\) Å (or less) to the angular limitaion of placing two beamports of width 0.05 m at distance 20 m apart.
Thermal neutrons have \(\lambda < 2\) Å, hence for these neutrons the critical angle of a \(m=1\) Ni guide, below which the neutrons would be reflected, would be less than \(\theta_c=0.2^\circ\). Since the geometrical limitation from two beamports of width 0.05 m placed 20 m apart is \(0.14^\circ\approx 0.2^\circ\), not much is gained by a guide, at least of this type for thermal or hot neutrons.