Problem:SANS q-range and resolution
Imagine a SANS instrument with a 1 m diameter PSD, a 40 mm diameter beam stop, pinhole collimation of diameter 20 mm (first) and 10 mm (at the sample), and equal collimation-detector lengths, \(R_{\rm c}=R_{\rm d}\), in the range 1-20 m.
Question 1
Calculate the \(q\)-range of this instrument for wavelengths of 4 Å and 20 Å.
What is the relation between \(q\) and the scattering angle. You can also find a relation between the possible scattering angles to detect between the beamstop and detector edge as a function of \(R_{\rm d}\) and and the radial position \(R\) on the detector.
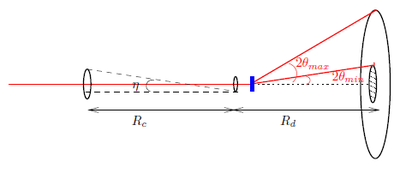
A sketch of the SANS instrument is shown in Figure xx--CrossReference--fig:sans_qrange_resolution--xx showing the relevant parameters for consideration of the SANS \(q\)-range and resolution.
The accesible scattering vector \(q\)-range is approximately proportional to the scattering angle range which is covered by the detector via
- \( q=\dfrac{4\pi}{\lambda}\sin{\theta} \)
In order to investigate small \(q\)'s the detector is moved further away from the sample since
- \( 2\theta = \tan^{-1}{\dfrac{R}{R_{\rm d}}}\)
where \(R\) is the radial position on the detector where the neutron hits and \(R_{\rm d}\) is the distance between the sample and detector. The smallest detectable scattering angle is limited by the radius of beamstop, i.e. \(R=0.02\) m yielding \(2\theta_{min}=0.057^\circ\) for \(R_{\rm d}\)=20 m. Whereas the largest scattering angle is limited by the radius of the detector i.e. \(R\)=0.50 m yielding \(2\theta_{max}=26.56^\circ\) for \(R_{\rm d}\)=1 m.
Hence according to the equations above for a particular wavelength \(\lambda \) of neutrons the smallest reachable \(q\) (i.e. \( q_{min}\)) is at \(R_d \)=20 m and the largest reachable \(q\) (i.e. \(q_{max}\) ) is at \(R_{\rm d}\)=1 m. Some values of the \(q\)-range are shown in Table xx--CrossReference--tab:Sans_qrange--xx.
Question 2
Calculate the maximum divergence of the incoming beam in the two extreme settings of \(R_{\rm c}\).
Since the height from lowest point of the second pinhole (diameter 0.01 m) to the top of the first pinhole (diameter 0.02 m) is 0.015 m the divergence is
- \( \eta = \tan^{-1}{\dfrac{0.015}{R_c}}\approx \dfrac{0.015}{R_c}\)
Which for a pinhole distance of \(R_c=20\) m gives the smallest divergence (best collimation) of \(\eta=0.00075\ \rm{rad}=0.043^\circ\), and for \(R_c=1\) m gives \(\eta=0.015\ \rm{rad}=0.86^\circ\)
Question 3
Calculate the relative uncertainty in the value of \(q\) due to the beam divergence, and compare to the total \(q\)-range in the two settings of \(R_{\rm c}\).
If we consider the wavelength of the neutrons to be well-defined (have a negligible uncertainty), the uncertainty in the determination of \(q\) is
- \( \delta q= \dfrac{\partial q}{\partial \theta} \delta \theta = \dfrac{4\pi}{\lambda}\cos{\theta}\ \delta \theta = q \dfrac{\delta \theta}{\tan{\theta}}\)
and since \(\delta \theta=\eta\) we have the relative uncertainty in \(q\)
- \( \dfrac{\delta q}{q}=\dfrac{\eta}{\tan \theta}\)
As it is seen from Table xx--CrossReference--tab:Sans_qerr--xx the extreme values of the relative uncertainty in \(q\) is approximately constant irrespective of the value of \(R_{\rm c}=R_{\rm d}\). The relative uncertainty in \(q\) is better at larger scattering angles.