Moderators
Neutrons produced in nuclear reactions typically have energies in the MeV regime. To be useful in materials research, the neutrons must have their energies reduced by many orders of magnitude.
We here describe the basics of this problem. For more information, a good introduction to neutron moderator physics is found in Ref. [1].
The moderation process
The neutron moderation is performed by a large number of successive collisions with a material that scatters strongly, but absorbs weakly. Here, hydrogen (H) is an almost perfect choice, also since its nuclear mass is similar to that of the neutron. This enables the H nucleus to absorb a large fraction of the neutron energy in each collision.
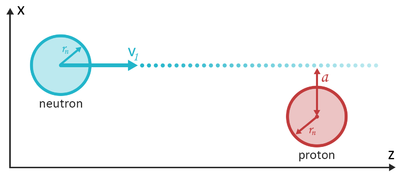
To show this, in a classical mechanics description, let us for simplicity consider the neutron and the protons as spherical particles with identical mass, \(m_{\rm n}\), and with identical radii, \(r_{\rm n}\). In the collision, we consider the proton to be at rest, and the neutron to move with the velocity \(v_1\) along the \(z\)-axis, and hence with a kinetic energy of \(E_1 = m_{\rm n} v_1^2 / 2\). The closest distance from the neutron trajectory to the proton center is denoted the impact parameter, \(a\), as seen in Figure xx--CrossReference--fig:moderation--xx. We consider the neutron to have a random trajectory, hence the probability for having a particular impact parameter, \(a\), is proportional to \(a\). If \(a<2r_{\rm n}\), a collision takes place.
We now define the \((x,z)\) plane to contain both the proton position and the neutron trajectory. After the scattering, the proton will remain in the plane, moving with the velocity \({\bf v}_{2,p}\). The proton trajectory makes an angle to the \(z\)-axis of
\begin{equation}\label{eq:moderator_angle} \sin\phi = \dfrac{a}{2r_{\rm n}}. \, \end{equation}
We denote the neutron velocity after the scattering by \({\bf v}_{2,n}\).
Now, energy conservation and momentum conservation in the \((x,z)\) plane gives three equations
\begin{align} m_{\rm n} v_1^2 &= m_{\rm n} (v_{2,p}^2 + v_{2,n}^2) \label{dummy1931789634}\\ m_{\rm n} v_1 &= m_{\rm n} (v^z_{2,p} + v^z_{2,n}) \label{dummy1425646361}\\ 0 &= m_{\rm n} (v^x_{2,p} + v^x_{2,n}) \label{dummy1897979680} \end{align}
and equation \eqref{eq:moderator_angle} give the fourth equation to determine the four unknowns components of \({\bf v}_{2,n}\) and \({\bf v}_{2,p}\). The solution for the velocity of the proton after the collision is
\begin{equation}\label{dummy870671655} v_{2,p} = v_1 \cos\phi . \, \end{equation}
The probability of reaching an impact parameter of \(a\) is proportional to \(a\) up to a value of \(2r_{\rm n}\). From this, we can calculate the average energy taken up by the proton in the collision. The result is
\begin{equation}\label{eq:E_half} E_{2,p} = \dfrac{E_1}{ 2} . \, \end{equation}
The proof of this is left to the reader, and is posed as the problem Hydrogen as a moderator.
A more detailed model will also provide the result that the neutron loses on average half of its energy per collision. Slowing the neutron energy by (a typical value of) 8 orders of magnitude, thus takes "only" 25-30 collisions. This is clearly within practical limits, since the typical mean free path in a hydrogen-rich material is of the order a few mm.
When the neutron energy becomes comparable to the (thermal) energy of the protons, the approximation of zero proton velocity breaks down, and a much more complex description is necessary, including the thermal motion of the proton and its surroundings. The effect is, nevertheless, that the neutrons quickly reach thermal equilibrium with the surrounding material.
Energy distribution of moderated neutrons
Most moderators consist of a tank with liquid water (H\(_2\)O; 300 K), which will slow down neutrons to roughly thermal equilibrium. When neutrons of lower energies are required, moderators of liquid hydrogen (H\(_2\); 30 K) or solid methane (CH\(_4\); 100 K) are used in connection with water pre-moderators. At ILL, there is even a hot moderator consisting of graphite at 2000 K. We will here discuss the implications of the moderator temperature.
Neutrons moderated at a temperature, \(T\), will ideally have a distribution of velocities, \(v\), given by the Maxwellian distribution of velocities, which is proportional to \(v^2\) times the Boltzmann factor \(\exp(-E_{\rm kin}/k_{\rm B}T)\). Since neutron emission through a (imaginary) hole at the moderator surface is essentially an effusion process, the intensity of neutrons from a beam port can be written as:
\begin{equation}\label{eq:maxwell_v} I(v) = I_0 v^{3} \exp\left(- \dfrac{m_{\rm n} v^2}{2 k_{\rm B} T}\right) , \end{equation}
where \(I_0\) is a constant proportional to the source power, \(k_{\rm B}\) is Bolzmann's constant, and the extra power of \(v\) comes from the effusion (faster particles have higher probability per time of leaving through the hole). The velocity distribution \eqref{eq:maxwell_v} peaks at \(v_{\rm max} = \sqrt{3 k_{\rm B}T/m_{\rm n}}\), corresponding to an energy of \(3 k_{\rm B} T / 2\).
It is customary to define the equivalent temperature of neutrons with a certain energy. The relation is given by
\begin{equation}\label{dummy1240073730} E = \dfrac{m_{\rm n} v^2}{2} = k_{\rm B} T_{\rm equiv} . \end{equation}
Describing the Maxwellian distribution in equation \eqref{eq:maxwell_v} in terms of wavelength requires some care. Since \(v = 2 \pi \hbar / (m_{\rm n} \lambda)\), we have \(dv = - 2 \pi \hbar d\lambda / (m_{\rm n} \lambda^2)\). Hence, the wavelength and velocity axes do not scale linearly, and a transformation of the distribution must be applied:
\begin{equation}\label{eq:maxwell_l} I(\lambda) \equiv \dfrac{dN}{d\lambda} = \dfrac{dN}{dv} \left| \dfrac{dv}{d\lambda}\right| = I'_0 \lambda^{-5} \exp\left(- \dfrac{2 \pi^2 \hbar^2}{\lambda^2 m_{\rm n} k_{\rm B} T}\right) , \end{equation}
where \(I_0' \propto I_0\) and \(N\) is the total number of neutrons. This distribution peaks at \(\lambda = 2 \pi \hbar \sqrt{3 / (5 m_{\rm n} k_{\rm B} T)}\), corresponding to \(E = 5 k_{\rm B} T / 3\). The energy equivalent of the peak value is thus changed by 10% between the two representations of the Maxwellian distribution due to the non-linear transformation, even though the two equations describe the same neutrons. Neutron moderator spectra are typically expressed in terms of the wavelength distribution, as illustrated in Figure xx--CrossReference--fig:maxwell--xx.
Moderator brilliance and the Liouville theorem
Since neutron scattering is mostly an intensity limited technique, an important quantity for a neutron source (a moderator) is the produced number of neutrons per unit of time. However, an even more useful number is the moderator brilliance, \(B\), which describes the produced number of neutrons per unit of time, per moderator area, per solid angle of flight direction, per wavelength interval. For example, a compact reactor core will have a higher brilliance than a less dense one, even though the total neutron production may be equal. In reality, the brilliance (or peak brilliance for pulsed sources) is almost the only relevant value for a neutron source. Brilliance is useful also at other positions in the neutron instrument, typically at the sample position, and has the same definition as above. In general \(B\) depends upon the position of the moderator, the time (for pulsed sources), and the direction and wavelength of the emitted neutrons
\begin{equation}\label{dummy1171737310} B=B(t,{\mathbf r},\hat{\mathbf v},\lambda) . \end{equation}
In terms of statistical mechanics, the brilliance is closely connected with phase space density, \(\phi({\bf r},{\bf v})\). This can be seen from the observation that \(\lambda\) can be written in terms of \(v\), and the position perpendicular to the main beam direction is given as \(z=vt\).
For an ensemble of particles undergoing only passive processes, the very powerful Liouville theorem is valid. It states that the phase space density cannot increase[2]. In the context of a neutron scattering instrument, this means that the brilliance at the neutron beam can under no circumstances be larger than that of the (brightest spot at the) moderator[3]. As a relevant example of this, focusing mirrors or lenses are somtimes used to bring more neutrons on to a small sample. According to the Liouville theorem, however, the increase in number of neutrons will come from an increase in the spread of their velocity directions (their divergence).
Real moderators

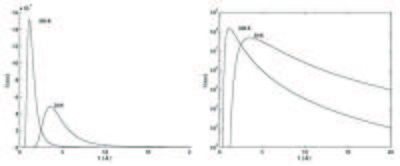
To improve transmission, real moderators have a limited thickness and hence do not moderate the neutrons completely. Their velocity distribution should rather be described by the sum of two or (most often) three Maxwellians, possibly with the addition of a tail towards high energies/low wavelengths, describing neutrons that are scattered only few times in the moderator. This is illustrated for the SINQ source at PSI in Figure xx--CrossReference--fig:SINQmoderators--xx. To avoid completely unmoderated neutrons from the source, the moderator geometry is chosen so that there is no line-of-sight between the place of neutron production and the beam port that opens out to the neutron scattering instruments.
Recent developments have shown that inhomogeneities in the moderator geometry, like holes and grooves, can locally enhance the neutron brilliance by up to a factor two, since these will generate a direct view to the moderator center, where the neutron density is larger[4]. However, design and detailed understanding of moderator systems is complex and is performed with the use of heavy nuclear physics simulations using codes like MCNPX and GEANT-4[5][6]. A description of this is beyond the scope of these notes. In the following, we will be satisfied with the existence of thermal and cold neutrons sources, and we will concentrate on the utilization of moderated neutrons.
- ↑ G.S. Bauer, Neutron Sources - Lecture Notes of the Introductory Course to the ECNS99, p. 12-26, (Report KFKI-1999-04/E)
- ↑ L.D. Landau and E.M. Lifshitz, Course in Theoretical Physics, vol. 5 Statistical Physics (Butterworth-Heinemann, 1951)
- ↑ K.H. Klenø, Exploration of the challenges of neutrons optics and instrumentation at long-pulsed spallation sources, Ph.D. thesis, Niels Bohr Institute, University of Copenhagen 2013 (submitted)
- ↑ D.J. Picton, S.M. Bennington, T.A. Broome, T.D. Benyon, Nucl. Instr. Meth. A 545, 363 (2005)
- ↑ E. Padovani, S.A. Pozzi, S.D. Clarke, E.C. Miller, MCNPX-PoliMi User's Manual, C00791 MNYCP, Radiation Safety Information Computational Center, Oak Ridge National Laboratory, 2012
- ↑ Geant 4.9.5 Physics Reference Manual, http://geant4.web.cern.ch/geant4/UserDocumentation/UsersGuides/PhysicsReferenceManual/BackupVersions/V9.5/fo/PhysicsReferenceManual.pdf, December 2012