Diffraction from crystalline materials
Our starting point for the description of crystal and powder diffraction is the expression for elastic scattering cross section for a system of nuclei, fixed in position, which we here repeat
\begin{equation}\label{eq:diffraction6} \dfrac{d\sigma}{d\Omega}\biggr|_{\rm nucl.} = \biggr|\displaystyle\sum_j b_j \exp(i {\mathbf q} \cdot {\mathbf r}_j)\biggr|^2 . \end{equation}
Our goal of this chapter is to describe the diffraction from crystals of macroscopic size and from nano-sized objects. Before this, we need to define some basic concepts in crystallography.
In the remainder of this section, however, we will expand equation \eqref{eq:diffraction6} to add the effect of material temperature on the scattered neutrons.
Scattering from vibrating nuclei
We release the artificial restriction that the nuclei are immobile. This means that the nuclear positions, \({\bf r}_j\) can change in time. We write the nuclear position as the sum of the average positions and a (small) time-dependent deviation:
\begin{equation}\label{eq:displacement} {\mathbf R}_j(t) = {\mathbf r}_j + {\mathbf u}_j(t) , \end{equation}
where the time average of the displacement vanish, \(\langle{\bf u}_j(t)\rangle=0\), in which the brackets denote the average. The full quantum mechanical treatment of equation \eqref{eq:displacement} results in an interaction between the neutrons and the quantised lattice vibrations, the phonons, which is studied by inelastic scattering. This is described on the Scattering from phonons page.
However, in this chapter we will consider only elastic scattering, so we can allow ourselves a more simple approach to estimate the effect of nuclear motion. Replacing \({\bf r}_j\) with \({\bf R}_j(t)\) in equation \eqref{eq:diffraction6}, we reach
\begin{align}\label{eq:diffraction7} \dfrac{d\sigma}{d\Omega} &= \left\langle \displaystyle\sum_{j,j'} b_j b_{j'} \exp(i {\mathbf q} \cdot {\mathbf R}_j(t)) \exp(-i {\mathbf q} \cdot {\mathbf R}_{j'}(t)) \right\rangle \\ &= \displaystyle\sum_{j,j'} b_j b_{j'} \exp(i {\mathbf q} \cdot {\mathbf r}_j) \exp(-i {\mathbf q} \cdot {\mathbf r}_{j'}) \left\langle \exp(i {\mathbf q} \cdot {\mathbf u}_j(t)) \exp(-i {\mathbf q} \cdot {\mathbf u}_{j'}(t)) \right\rangle . \nonumber \end{align}
The vibration term in the brackets implies that the phase of the scattered neutron has a slight random variation. This has the effect of reducing the scattering intensity. To quantify this, we assume that the displacements are uncorrelated, \(\langle{\bf u}_j(t){\bf u}_{j'}(t)\rangle=0\), and that the displacement amplitudes are isotropic and equal, \(\langle{\bf u}_j(t)^2\rangle=\langle{\bf u}_{j'}(t)^2\rangle\). Then, we perform a second order series expansion of the complex exponential functions:
\begin{align}\label{eq:diffraction8} \left\langle \exp(i {\mathbf q} \cdot {\mathbf u}_j(t)) \exp(-i {\mathbf q} \cdot {\mathbf u}_{j'}(t)) \right\rangle & \approx \left\langle \left(1-i {\mathbf q} \cdot {\mathbf u}_j(t) - ({\mathbf q} \cdot {\mathbf u}_j(t))^2/2\right) \left(1+i {\mathbf q} \cdot {\mathbf u}_{j'}(t) - ({\mathbf q} \cdot {\mathbf u}_{j'}(t))^2/2\right)\right\rangle \\ &\approx \left\langle 1-({\mathbf q} \cdot {\mathbf u}_j)^2 \right\rangle \nonumber\\ &\approx \exp(- \langle {\mathbf q} \cdot {\mathbf u}_j \rangle^2) .\nonumber \end{align}
The fourth (and higher) order terms in the series expansion agrees with the final result above, provided the displacement term \(\mathbf q \cdot {\bf u}_j(t)\) follows a normal distribution.
The Debye-Waller factor
The correction term equation \ref{eq:diffraction8} is widely known as the Debye-Waller factor:
\begin{equation}\label{eq:diffraction_DW} \exp(-2W_j) = \exp(-\langle{\mathbf q} \cdot {\mathbf u_j} \rangle^2). \end{equation}
In general, the Debye-Waller factor is site-dependent. However, one often uses the approximation where \(\exp(-2W_j)\) is the same for all \(j\). In this case, the elastic nuclear scattering cross section reads:
\begin{equation}\label{eq:diffract2} \dfrac{d\sigma}{d\Omega} \biggr|_{\rm nucl.} = \exp(-2W) \biggr| \displaystyle\sum_{j} b_j \exp(i {\mathbf q} \cdot {\mathbf r}_j)\biggr|^2 . \end{equation}
This implies that the expression in equation \ref{eq:diffraction6} for immobile nuclei still holds, with the correction that we need to multiply by the site-independent Debye-Waller factor, \(\exp(-2W)\).
At low temperatures, the temperature dependent displacement \({\bf u}_j\) has a small, but non-zero value due to zero-point fluctuations. This means that the Debye-Waller factor is always smaller than (but often close to) unity. All this is described in much more detail on the Scattering from lattice vibrations page and e.g. in the textbook by Squires[1].
Experimental consideration
The \(q\)-dependence of the Debye-Waller factor means that for large values of \(q\) (above 10 Å\(^{-1}\)), one generally prefers to cool the sample to avoid losing signal.
On the other hand, as \(q \rightarrow 0\) the Debye-Waller factor goes quickly to unity. This means that this temperature-dependent factor can be neglected in SANS, as already anticipated on the SANS page.
The scattering cross section for a crystal
We can now calculate the expression for the elastic neutron cross section, equation \eqref{eq:diffract2}, for a crystal, where we index the unit cells by \(j\) and the atoms within the unit cells by \(i\):
\begin{equation}\label{dummy1681181848} \dfrac{d\sigma}{d\Omega}\biggr|_{\rm nucl.\,el.} = \exp(-2W) \biggr|\displaystyle\sum_{i,j} b_i \exp(i {\mathbf q} \cdot ({\mathbf r}_j+{\mathbf\Delta}_i)) \biggr|^2 . \end{equation}
A small rearrangement of terms leads to the basic equation for crystal diffraction:
\begin{equation}\label{eq:cross_diffract_basis} \dfrac{d\sigma}{d\Omega}\biggr|_{\rm nucl.\,el.} = \exp(-2W) \left| F_{\rm N}({\mathbf q})\right|^2 \biggr|\displaystyle\sum_{j} \exp(i {\mathbf q} \cdot {\mathbf r}_j) \biggr|^2 , \end{equation}
where the nuclear structure factor, given by
\begin{equation}\label{eq:structurefactor} F_{\rm N}({\mathbf q})=\displaystyle\sum_{i} b_i \exp(i {\mathbf q} \cdot {\mathbf\Delta}_i), \end{equation}
depends only on the arrangement of the atoms inside the unit cell. We will later see that it is possible to determine \(|F_{\rm N}({\bf q})|^2\) experimentally and use it to deduce the atomic positions.
The lattice sum
To proceed, we like to calculate the sum over all unit cells: \(|\sum_j \exp(i {\bf q} \cdot {\bf r}_j)|^2\), also known as the lattice sum. Let us as a start approach this intuitively. If \(\bf q\) equals a reciprocal lattice vector, \(\bf\tau\), all the complex exponentials equal unity, c.f. equation \eqref{eq:lattice_phase_2pi}, and the squared sum must equal \(N^2\), where \(N\) is the number of unit cells. If \(\bf q\) is not a reciprocal lattice vector, many complex phases are present, and the sum should be small compared to \(N^2\) or vanish completely. Let us show formally that this is indeed what happens.
We assume that the lattice is "infinite", but we keep counting the number of lattice sites by \(N\). Hence, the squared sum can be rewritten
\begin{align} \label{eq:latticesum} \biggr|\displaystyle\sum_j \exp(i {\mathbf q} \cdot {\mathbf r}_j) \biggr|^2 &= \displaystyle\sum_{j,j'} \exp(i {\mathbf q} \cdot ({\mathbf r}_j-{\mathbf r}_{j'})) \\ &= \displaystyle\sum_{j,l} \exp(i {\mathbf q} \cdot {\mathbf r}_l) \nonumber\\ &= N \displaystyle\sum_l \exp(i \mathbf q \cdot {\mathbf r}_l) \nonumber \\ &= N \displaystyle\sum_j \exp(i \mathbf q \cdot {\mathbf r}_j). \end{align}
To perform the middle step, we utilize that the double lattice sum over \({\bf r}_j\) and \({\bf r}_{j'}\) can be transformed to a double sum over (i) one site, \({\bf r}_j\), and (ii) the difference between sites, \({\bf r}_l = {\bf r}_j - {\bf r}_{j'}\).
Now, equation \eqref{eq:latticesum} has the form \(|x|^2 = Nx\). Solving for the unknown lattice sum, \(x\), there are two possible solutions: \(N\) and \(0\). The value can only be \(N\) when all complex phases are multipla of \(2\pi\). Hence, this solution is found only when \(\bf q\) equals a reciprocal lattice vector; otherwise the zero solution must be chosen, as conjectured above. We can thus write equation \eqref{eq:latticesum} as a sum of Kronecker delta functions:
\begin{equation}\label{dummy1647858657} \displaystyle\sum_j \exp(i {\mathbf q} \cdot {\mathbf r}_j) = N \displaystyle\sum_{\boldsymbol\tau} \delta_{ {\mathbf q},{\boldsymbol\tau}} . \end{equation}
However, it is more convenient to write \eqref{eq:latticesum} in terms of Dirac delta functions. To do this, we write the sum as an unknown constant, \(c\), times the delta function:
\begin{equation}\label{eq:latticesum_c} \displaystyle\sum_j \exp(i {\mathbf q} \cdot {\mathbf r}_j) = c \displaystyle\sum_{\boldsymbol\tau} \delta ({\mathbf q} - {\boldsymbol\tau}) . \end{equation}
To determine the constant \(C\), we now integrate over one unit cell of the reciprocal lattice - a Brillouin zone. The right hand side can be immediately integrated to give \(c\), since the integration volume by definition contains exactly one reciprocal lattice vector. The left hand side is more elaborate; first we exchange sum and integration
\begin{equation}\label{eq:BZ_sum_int} \displaystyle\int_{\rm BZ} \displaystyle\sum_j \exp(i {\mathbf q} \cdot {\mathbf r}_j) d{\mathbf q} = \displaystyle\sum_j \displaystyle\int_{\rm BZ} \exp(i {\mathbf q} \cdot {\mathbf r}_j) d{\mathbf q} . \end{equation}
Now, the integral on the right hand side vanish if \({\bf r}_j \neq 0\). This can be seen by writing \({\bf r}_j = n_a {\bf a} + n_b {\bf b} + n_c{\bf c}\), \({\mathbf q} = h {\bf a}^* + k {\bf b}^* + l {\bf c}^*\), and integrate over \(h\), \(k\), and \(l\) (which are here no longer integers). The first one-dimensional integral is of the form \(\int_0^1 \exp(i h {\bf a}^* \cdot {\bf r}_j) dh = \int_0^1 \exp(i h n_a 2\pi ) dh = \delta_{n_a,0}\), and similar for the \(k\) and \(l\) integrals. Hence, the only contribution comes from the term with \({\bf r}_j = 0\). Therefore, the right hand side of equation \eqref{eq:BZ_sum_int} simply gives the volume of the Brillouin zone:
\begin{equation}\label{eq:BZ_integral} \displaystyle\sum_j \displaystyle\int_{\rm BZ} \exp(i {\mathbf q} \cdot {\mathbf r}_j) d{\mathbf q} = V_{\rm r} = \dfrac{(2\pi)^3}{V_0} = c . \end{equation}
Combining equation \eqref{eq:cross_diffract_basis}, \eqref{eq:latticesum}, \eqref{eq:latticesum_c}, and \eqref{eq:BZ_integral}, the final equation for neutron diffraction from a crystal becomes
\begin{equation}\label{eq:diffract} \dfrac{d\sigma}{d\Omega} \biggr|_{ {\rm nucl. el.}} = N \dfrac{(2\pi)^3}{V_0}\exp(-2W) \left| F_{\rm N}({\mathbf q})\right|^2 \displaystyle\sum_{ {\boldsymbol\tau}} \delta({\mathbf q}-{\boldsymbol\tau}). \end{equation}
The Bragg law
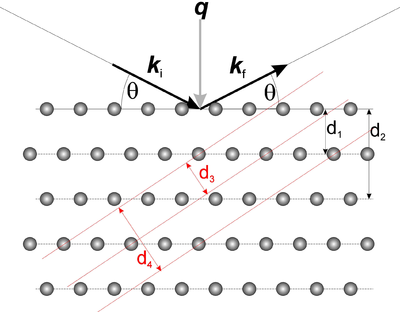
We now turn to the qualitative understanding of the diffraction cross section in equation \eqref{eq:diffract}. The delta-function in the equation gives rise to the so-called Laue condition
\begin{equation}\label{dummy642626747} {\mathbf q} = {\boldsymbol\tau} . \, \end{equation}
This can also be expressed in terms of the lattice spacings, \(d\), associated with the reciprocal lattice vectors (defined in equation \eqref{eq:latticespacing}): through the Bragg law:
\begin{equation}\label{eq:bragg} n \lambda = 2 d \sin(\theta) ,\, \end{equation}
where \(n\) is a positive integer and \(\theta\) is the angle between the incoming neutron direction and the lattice planes, see Figure xx--CrossReference--fig:bragg--xx. When scattering from a certain set of lattice planes, the scattering is specular, i.e. the incident angle equals the outgoing angle. The proof of equation \eqref{eq:bragg} is left as problem Simple Bragg scattering, the monochromator. The essence of the Bragg law is: Diffraction takes place only when equation \eqref{eq:bragg} is fulfilled. However, the reverse is not always the case. Sometimes no neutrons are diffracted even though the Bragg condition is fulfilled. This happens for reflections with \(|F_{\rm N}(\bf q)|^2=0\), as illustrated e.g. in problem Bragg scattering from Bravais lattices.
Experimental considerations
When a crystal is oriented to fulfill Bragg's law, one often talks about the reflected neutrons as a Bragg peak or a Bragg reflection. The neutron intensity in a Bragg reflection can be considerable, and at times the neutron beam needs to be attenuated in order not to saturate the detector(s). Saturation effects start at around \(10^4\) to \(10^6\) counts per second, depending on detector details. Most often, the attenuation is performed in the incident beam, often by using plastic sheets, possibly with boron content.
The angle between the incoming and outgoing beam in Figure xx--CrossReference--fig:bragg--xx is seen to be \(2\theta\). This is denoted the scattering angle and is the primary observable to be measured in an experiment. Usually in diffraction experiments, this angle needs to be determined to precisions of the order \(0.01^\circ\).
Integrals over the diffraction cross section
For the quantitative understanding of equation \eqref{eq:diffract}, the Dirac \(\delta\)-function in the cross section is the crucial part. The infinite amplitude of the \(\delta\)-function should not be taken litterally, since infinite amplitudes are unphysical. Instead, the \(\delta\)-function symbolizes that the scattering is strongly peaked at very small intervals around the reciprocal lattice vectors. The integral of the \(\delta\)-function does, however, have physical significance. Neutron scattering experiments are performed in non-ideal conditions, e.g. the incoming beam has a slight variation in wavelength (0.1\% - 1\%) and has a finite divergence (\(0.1^\circ\) - \(1^\circ\)). In most cases, this makes the observed intensity depend on the integral over the scattering cross section. We will here show how to perform integrals over the \(\delta\)-function. The derivation below is strongly inspired by Squires[1].
We will calculate the total cross section, i.e. the integral over all neutrons scattered by a particular Bragg peak.
\begin{equation}\label{eq:sigma_bragg_integral} \sigma_{\boldsymbol\tau} = \displaystyle\int \left( \dfrac{d\sigma}{d\Omega}\right)_{\rm nucl. el.,\, {\boldsymbol\tau}} d\Omega . \end{equation}
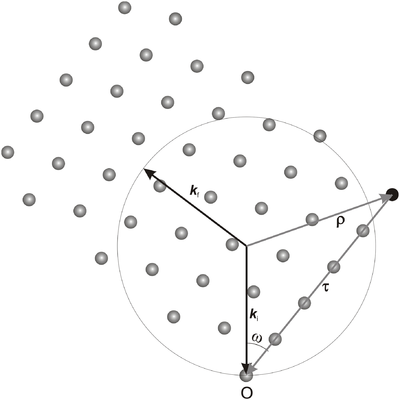
We consider a situation where the incoming neutron wave vector, \({\bf k}_{\rm i}\), and the reciprocal lattice vector in question, \(\bf\tau\), are fixed. The angle between \({\bf k}_{\rm i}\) and \(\bf\tau\) determines (one part of) the crystal orientation; this angle is most often denoted \(\omega\). The plane spanned by the two vectors \({\bf k}_{\rm i}\) and \(\bf\tau\) is called the scattering plane. The experimental geometry is often arranged so that the scattering plane is the horizontal plane. The factor \(\delta(\mathbf q-\boldsymbol\tau)\) in the scattering cross section in equation \eqref{eq:diffract} implies that the outgoing wave vector, \({\bf k}_{\rm f}\), also lies in the scattering plane, see Figure xx--CrossReference--fig:scatteringplane--xx. For very small crystallites, however, a spread of \({\bf k}_{\rm f}\) is seen, both in the in-plane and the out-of-plane directions. This is discussed in the section Diffraction from nano-sized systems.
The integral in equation \eqref{eq:sigma_bragg_integral} boils down to an integral over the \(\delta\)-function:
\begin{equation}\label{eq:delta_integral_1} \displaystyle\int \delta({\mathbf q}-{\boldsymbol\tau}) d\Omega = \displaystyle\int \delta(\boldsymbol\rho - {\mathbf k}_{\rm f}) d\Omega , \end{equation}
where we define \(\boldsymbol\rho = {\mathbf k}_{\rm i} - \boldsymbol\tau \). The only variable in the integral is the direction of \({\bf k}_{\rm f}\), since the requirement of elastic scattering gives \(|{\bf k}_{\rm i}|=|{\bf k}_{\rm f}|\). To calculate the two-dimensional integral over the three-dimensional \(\delta\)-function, we employ a small trick. We first observe that the \(\delta\)-function contributes only when
\begin{equation}\label{eq:delta_integral_2} |\boldsymbol\rho|=|{\mathbf k}_{\rm f}| . \end{equation}
To be more precise: whenever equation \eqref{eq:delta_integral_2} is fulfilled, the integral in equation \eqref{eq:delta_integral_1} will be non-zero. One could say that the crystal "chooses" one orientation of \({\bf k}_{\rm f}\) (or one solid angle \(d\Omega\)) that fulfills the scattering condition of equation \eqref{eq:delta_integral_2}. We can therefore write
\begin{equation}\label{dummy1878593029} \displaystyle\int \delta(\boldsymbol\rho - {\mathbf k}_{\rm f}) d\Omega = -c' \delta(k_{\rm i}^2+\tau^2-2k_{\rm i}\tau\cos(\omega)-k_{\rm f}^2) , \end{equation}
where \(c'\) is a constant to be determined in the following. To proceed, we note that the integral of a \(\delta\)-function over the full 3-dimensional space is unity. This leads to
\begin{align} 1 &= \displaystyle\int \delta(\boldsymbol\rho - {\mathbf k}_{\rm f}) d{\mathbf k}_{\rm f} \label{dummy854105364}\\ &= \displaystyle\int \left( \displaystyle\int \delta(\boldsymbol\rho - {\mathbf k}_{\rm f}) d\Omega \right) k_{\rm f}^2 dk_{\rm f} \nonumber\\ &= \displaystyle\int c' \delta(k_{\rm i}^2+\tau^2-2k_{\rm i}\tau\cos(\omega)-k_{\rm f}^2) k_{\rm f}^2 dk_{\rm f} \nonumber\\ &= \dfrac{c'\rho}{2} .\nonumber \end{align}
where \(\rho^2 = k_{\rm i}^2 + \tau^2 - 2 k_{\rm i}\tau\cos(\omega) = k_{\rm f}^2\). Hence, we can determine \(c'\)
\begin{equation}\label{dummy1236443606} c' = \dfrac{2}{\rho} = \dfrac{2}{k_{\rm f}} . \end{equation}
In this derivation, we have implicitly used equation \eqref{eq:delta_integral_2}. Now that the integrals are dealt with, we can impose the condition of elastic scattering, \(k_{\rm i} = k_{\rm f}\), and use equation \eqref{eq:diffract} to reach the expression for the integrated cross section
\begin{equation}\label{eq:bragg_half_int} \sigma_{\boldsymbol\tau} = \dfrac{N (2\pi)^3}{V_0} \dfrac{2}{k_{\rm i}} \exp(-2W) \left| F_{\rm N}(\tau)\right|^2 \delta(\tau^2-2k_{\rm i}\tau\cos(\omega)). \end{equation}
This equation still contains a \(\delta\)-function and thus needs additional integration (over the crystal orientation, \(\omega\), or the initial wave vector, \({\bf k}_{\rm i}\)) to make physical sense. Hence, equation \eqref{eq:bragg_half_int} is only a stepping stone to calculate the cross sections for some particular experimental arrangements. These are discussed in the sections Diffraction from single crystals with monochromatic radiation, Diffraction from a powder, and Diffraction from nano-sized systems.