Basic crystallography
We here give a brief introduction to the scientific field of crystallography, which is the study of the atomic arrangements in crystals, often seen in connection with organic and inorganic chemistry, mineralogy, or molecular biology (protein crystallography). Crystallography is a vast field in itself, and here we only touch the basics of it.
Crystal structures consist of ordered arrangements of groups of atoms (or molecules) placed within two- or three-dimensional space filling lattices. The overall symmetry of a crystal structure is determined by the underlying crystal lattice and by application of certain symmetry elements. In mathematical terms, these symmetry elements are called congruent, isometric transformations. They may be translations, rotations and screws (direct congruent) or inversions, reflections and glides (opposite congruent). See Ref. [1] for further details.
Lattice vectors
In a regular crystal, the atoms are arranged in a three-dimensional periodic structure; a lattice. It is possible to divide the crystal into a (large) number of identical unit cells, each containing one or more atoms. The position of a unit cell can be determined by just three integers, \(n_a\), \(n_b\), and \(n_c\):
\begin{equation}\label{eq:r_unitcell} {\mathbf r} = n_a {\mathbf a} + n_b {\mathbf b} + n_c {\mathbf c} , \end{equation}
where the vectors \({\bf a}\), \({\bf b}\), and \({\bf c}\) are called the lattice vectors. The length of the lattice vectors are called the lattice constants, \(a\), \(b\), and \(c\), respectively. Usually, but not always, the order is chosen so that \(a \leq b \leq c\).
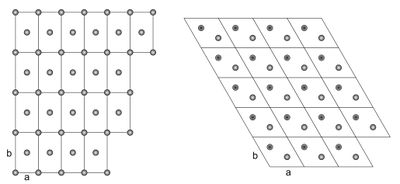
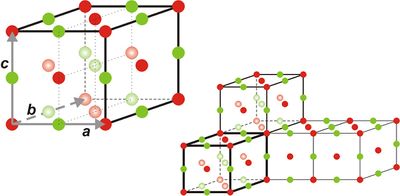
Two-dimensional crystal lattices are simple to visualise, and two examples are shown in Figure xx--CrossReference--fig:2Dcrystal--xx. More realistic crystal lattices are three-dimensional, where the shape of a unit cell is a parallelepiped spanned by the three (right handed) lattice vectors, as shown in Figure xx--CrossReference--fig:crystal--xx. The angles in the unit cell are defined with \(\alpha\) being the angle between \({\bf b}\) and \({\bf c}\), \(\beta\) being the angle between \({\bf c}\) and \({\bf a}\), and \(\gamma\) the angle between \({\bf a}\) and \({\bf b}\). The volume of a unit cell is given by the volume product
\begin{equation}\label{dummy1375896635} V_0 = {\mathbf a} \cdot {\mathbf b} \times {\mathbf c}. \end{equation}
This product is positive due to the right-handedness of the lattice vectors.
The reciprocal lattice
It is convenient to define the reciprocal lattice vectors by
\begin{equation}\label{dummy1014747689} {\mathbf a}^* = \dfrac{2 \pi}{V_0} {\mathbf b} \times {\mathbf c} , \qquad {\mathbf b}^* = \dfrac{2 \pi}{V_0} {\mathbf c} \times {\mathbf a} , \qquad {\mathbf c}^* = \dfrac{2 \pi}{V_0} {\mathbf a} \times {\mathbf b} . \end{equation}
Each reciprocal lattice vector is perpendicular to two of the three real-space lattice vectors:
\begin{equation}\label{dummy60639701} {\bf a}^* \cdot {\bf b} = {\bf a}^* \cdot {\bf c} = 0 , \qquad {\bf b}^* \cdot {\bf a} = {\bf b}^* \cdot {\bf c} = 0 , \qquad {\bf c}^* \cdot {\bf a} = {\bf c}^* \cdot {\bf b} = 0 , \end{equation}
whereas
\begin{equation}\label{dummy1842204777} {\bf a}^* \cdot {\bf a} = 2\pi , \qquad {\bf b}^* \cdot {\bf b} = 2\pi , \qquad {\bf c}^* \cdot {\bf c} = 2\pi . \end{equation}
The three reciprocal lattice vectors span the reciprocal lattice, where a general lattice point is given by
\begin{equation}\label{eq:rlv} {\boldsymbol\tau}_{hkl} = h {\mathbf a}^* + k {\mathbf b}^* + l {\mathbf c}^* . \end{equation}
The Miller indices \(h\), \(k\), and \(l\) are here integers. The lattice spacing corresponding to a set of Miller indices is defined as the distance between lattice planes perpendicular to \({\bf\tau}_{hkl}\) and is given by
\begin{equation}\label{eq:latticespacing} d_{hkl} = \dfrac{2 \pi}{|{\boldsymbol\tau}_{hkl}|} . \end{equation}
From equation \eqref{eq:r_unitcell} and \eqref{eq:rlv}, we calculate the dot product between a general lattice vector and a general vector of the reciprocal lattice:
\begin{equation}\label{eq:lattice_phase_2pi} {\boldsymbol\tau}_{hkl} \cdot {\mathbf r} = 2 \pi (n_a h + n_b k + n_c l) . \end{equation}
This result will be used in later derivations.
It can easily be shown that the volume of the reciprocal unit cell is given by
\begin{equation}\label{dummy310262986} V_{\rm r} = \dfrac{(2\pi)^3}{V_0}. \end{equation}
It is possible to make a reciprocal space unit cell of volume \(V_{\rm r}\), which is centered around the origin and in which each point is located closer to the origin than to any reciprocal lattice vector. This cell is called the Brillouin zone and is discussed in detail in most textbooks on solid state physics[2].
Atomic positions in the unit cell
A particular simple class of lattices is the Bravais lattice, defined as a lattice where each unit cell contains only one atom. Hence, a Bravais lattice are found only among the pure elements, since each unit cell must contain at least one formula unit. In a Bravais lattice, the atomic positions are given directly by equation \eqref{eq:r_unitcell}.
By far, most lattices are non-Bravais lattices. Here, each unit cell consists of more than one atom, and their relative positions within the unit cell are given by their basis, denoted \(\bf\Delta\). The absolute position of the \(i\)'th atom in the \(j\)'th unit cell is thus
\begin{equation}\label{dummy404727957} {\mathbf r}_{i,j} = {\mathbf r}_j + {\boldsymbol\Delta}_i , \end{equation}
where \({\bf r}_j\) is the position of the \(j\)'th unit cell.
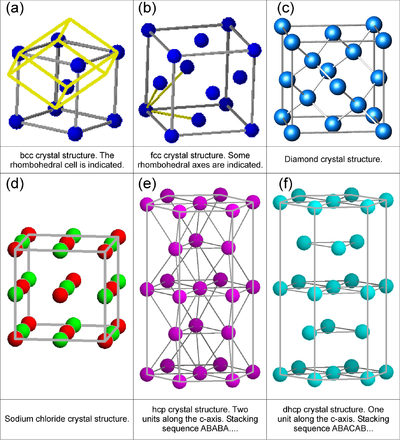
One often encountered example of a lattice with a basis is the body-centered cubic lattice (see Figure xx--CrossReference--fig:crystal_classes--xx). This lattice can be described as a simple cubic lattice of side length \(a\) with a two-atom basis. One atom is placed at \({\bf\Delta}_0 = (0,0,0)\), and the other at \({\bf\Delta}_1 = (1/2, 1/2, 1/2)\,a\).
Symmetry groups
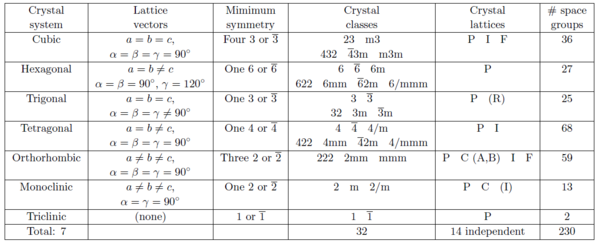
According to the symmetry properties, ordered arrangements of atoms are divided into 17 two-dimensional and 230 three-dimensional space groups. Below we describe the 7 groups of crystal lattices covering all three-dimensional space-groups sorted by decreasing symmetry. The meaning of the parenthesized letters after the lattice names will be explained later.
- Cubic: (P, I, or F). This is the class of highest symmetry and has a 4-fold symmetry. All lattice constants are equal, and the lattice vectors are mutually perpendicular. Thus, the unit cells are cubes: \(a=b=c\), \(\alpha = \beta = \gamma = 90^\circ\).
- Hexagonal (P). This is a crystal class with a 6-fold symmetry axis: \(a= b \neq c\), \(\alpha = \beta = 90^\circ\), and \(\gamma = 120^\circ\).
- Trigonal (R). This can be seen as an angular distortion of the cubic lattice. Trigonal structures are often described by hexagonal cells with the \(c\)-axis along the rhombic body diagonal: \(a=b=c\), \(\alpha = \beta = \gamma \neq 90^\circ\).
- Tetragonal (P or I). This class can be seen as a distortion of a the cubic crystal along one axis, keeping all vectors perpendicular: \(a=b \neq c\), \(\alpha = \beta = \gamma = 90^\circ\).
- Orthorhombic (P, C, I, or F). This is a further distortion of a tetragonal crystal, still keeping the unit vectors perpendicular: \(a \neq b \neq c\), \(\alpha = \beta = \gamma = 90^\circ\).
- Monoclinic (PB or PC). An angular distortion of an orthorhombic crystal: \(a \neq b \neq c\), \(\alpha = \beta = 90^\circ\), \(\gamma \neq 90^\circ\).
- Triclinic (P). The lowest symmetry class, where the lattice is a parallelepiped without any relation between axis and angles: \(a \neq b \neq c\), \(\alpha \neq 90^\circ\), \(\beta \neq 90^\circ\), \(\gamma \neq 90^\circ\).
Crystal structures and symmetries
The knowledge of the classification in 230 space groups is highly useful when determining crystal structures. Details of the symmetry aspects of these space-groups are collected in various versions of "The International Tables for Crystallography" (in this text abbreviated "IT")[3][4]-->. Here, we will give a rudimentary introduction to three-dimensional crystal structures and their classification. Furthermore describe how to interpret the information given in IT and how to use it when refining a crystal structure from real experimental or simulated diffraction data.
In its simplest form, a crystal structure is formed by placing one atom within a lattice and applying a number of symmetry elements which are consistent with the geometry of the underlying lattice to the coordinates of the first atom. Naturally, the symmetry of the structure increases with the number of symmetry elements. In [3], the site positions of atoms in the possible two- and three-dimensional space groups are listed according to the crystal lattices and the applied symmetry elements.
The space group with the lowest symmetry and space group number "1" is triclinic P1. Within the unit cell this space group has just one atom site position per atom type with coordinates \((x,y,z)\). The symmetry element is a translation of the unit cell or, equivalently, rotation by 360\(^\circ\). The space group with the second lowest symmetry (translation of the unit cell) and space group number "2" is also triclinic \(\text{P}\bar{1}\), but in addition to translation symmetry it has an inversion centre. Hence, within the unit cell this space group has two atom site positions per atom type with general coordinates \((x,y,z)\) and \((-x,-y,-z)\).
The space group with the highest symmetry and space group number 230 is cubic \(Ia\bar{3}d\). Within the unit cell this space group has 96 atom sites per atom type. The set of 96 coordinates \((x_i, y_i, z_i)\) are generated by the coordinates of a single atom site per atom type \((x_1,y_1,z_1)\) after application of the space group symmetry elements (see the section How to use the information in IT).
Each of the space group listings in IT are described by a number and a combination of letters and numbers. The numbers represent the rotational symmetry (1-, 2-, 3-, 4- or 6-fold rotation) of the space group and small letters represent certain symmetry elements (e.g. m for mirror line or plane and represent 1- or 3-fold rotations plus inversions through centre). The first letter is always a capital. It indicates if some vectors in the crystal lattice are related in a non-trivial way and possess symmetry other than the identity. These letters are shown in parenthesis in the listing (1 to 7) of the lattice types given above. The letter P means primitive, i.e. the only symmetry imposed by the lattice is the identity, F means face centered, i.e., for the smallest possible unit cell, the lattice symmetry automatically generates atom sites at \((x,y,z) + \bar{d}_f\) where \(\bar{d}_f\) equals half a face diagonal. The letter I means body centered, which is a translation from German "innen zentrierte", i.e. the lattice symmetry automatically generates atom sites at \((x,y,z) + \bar{d}_b\) where \(\bar{d}_b\) equals half a body diagonal. For more complicated crystal lattices, other capitals are used to signify specific lattice related symmetries. The most important ones are R (rhombohedral) used for trigonal space groups and C (base centered) used for some orthorhombic and monoclinic space groups.
Figure xx--CrossReference--fig:crystal_classes--xx(a) shows a body centered cubic (bcc) structure. Figures xx--CrossReference--fig:crystal_classes--xx(b) and (d) illustrate face centered cubic (fcc) structures with one and two types of atoms, respectively. Figures xx--CrossReference--fig:crystal_classes--xx(a) and (b) also represent two of the 14 three-dimensional Bravais lattices. By definition, Bravais lattices contain only a single atom per unit cell which is obviously not the case for the cubic structures shown in Figure xx--CrossReference--fig:crystal_classes--xx(a) and (b). However, the smallest space filling units for fcc and bcc mono-atomic crystals are not cubic, but rhombohedral as shown by the true yellow unit cell in Figure xx--CrossReference--fig:crystal_classes--xx(a) and indicated by the three yellow rhombohedral axes shown in Figure xx--CrossReference--fig:crystal_classes--xx(b). The bcc and fcc Bravais structures are to be considered in more detail in the problem Bragg scattering from Bravais lattices. Certain properties of structures with non-Bravais lattices will be considered in the problem Bragg scattering from non-Bravais lattices.
Another important structure is the hexagonal closed packed (hcp) lattice, which is a cell with a two-atom basis. Regarding the hcp lattice, it is important to notice that the distance between all nearest neighbour atoms are equal, and that it represents the closest possible packing of spheres (a property it shares with the fcc lattice). The hcp crystal will also be treated in the problem Bragg scattering from Bravais lattices.
The crystal classes and space groups
To provide a systematic overview, we will show Table xx--CrossReference--tab:crystallographytable--xx that contains the 7 crystal systems, the 14 crystal lattices, the 32 crystal classes, and how they are distributed on the 230 space groups. This table should be considered a "roadmap" to explore the world of crystallography, as presented in detail in IT and a lot of other places in literature.
How to use the information in IT

To refine diffraction data with standard programs, you need information about the possible atom positions in the simulated structure and their approximate occupancies. An explanation of how to obtain this information by means of "IT" is given in the following and can be used to solve Simulation project: A powder diffractometer.
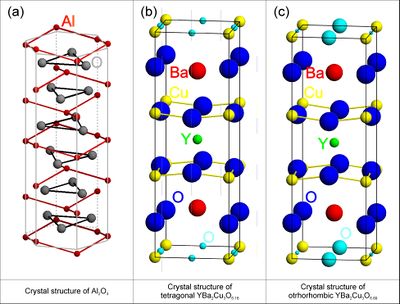
Before attempting a structure refinement, you will usually know the chemistry of your sample and have a rough idea about the crystal structure from other works (publications or databases) either obtained in the form of X-ray or neutron diffraction experimental data or, more unusual, from clever guesses. If the structure is known from publications the information may be in the form of a space group name or number. This is, e.g, the case for the tetragonal phase of the high-temperature superconductor YBa\(_2\)Cu\(_3\)O\(_{6+x}\) shown in Figure xx--CrossReference--fig:crystal_classes2--xx(b) for \(x = 0.18\), (P4/mmm, (\(D^1_{4h}\)), or #123, see Figure xx--CrossReference--fig:ITpage2--xx) with lattice parameters \(a = b \neq c\) and \(\alpha = \beta = \gamma = 90^\circ\). The coordinates of the atoms are called site positions and written in an abbreviated form which will be described shortly. For YBa\(_2\)Cu\(_3\)O\(_{6+x}\) the site positions are: Y-atoms at (\(1d\)), Ba-atoms at (\(2h\)), Cu-atoms at (\(1a\)) and (\(2g\)), and O-atoms at (\(2f\)), (\(2g\)), and (\(4i\)).
Depending on the O-concentration, \(x\), and the temperature, YBa\(_2\)Cu\(_3\)O\(_{6+x}\) undergoes a structural phase change from the tetragonal structure to an orthorhombic structure. The corresponding description of the orthorhombic structure usually named YBa\(_2\)Cu\(_3\)O\(_{7-x}\) is shown in Figure xx--CrossReference--fig:crystal_classes2--xx(c) for \(x = 0.11\). The space group is Pmmm, (\(D^1_{2h}\)), or #47 (see Figure xx--CrossReference--fig:ITpage--xx) with lattice parameters \(a \neq b \neq c\) and \(\alpha = \beta = \gamma = 90^\circ\). The possible site positions for the atoms in YBa\(_2\)Cu\(_3\)O\(_{7-x}\) are as follows: Y-atoms at (\(1h\)), Ba-atoms at (\(2t\)), Cu-atoms at (\(1a\)) and (\(2q\)) and O-atoms at (\(1b\)) or (\(1e\)), (\(2q\)), (\(2r\)), and (\(2s\)).
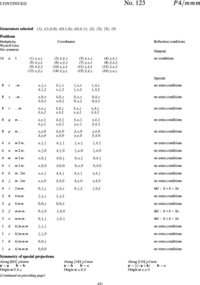
In order to explain the meaning of the parenthesised number/letter codes for the site positions quoted above, we use the space group example in Figure xx--CrossReference--fig:ITpage_old--xx. The figure lists the possible coordinates of atoms in the (fcc) cubic space group #225, \(Fm\bar{3}m\), or (\(O^5_h\)). The first column to the left shows the number of atoms with coordinates listed in columns 4 to 9. Because of the space group symmetry, one general atom coordinate set \((x,y,z)\) results in 191 other atom coordinates (192 general sites) unless there are special relations between \(x\), \(y\), and \(z\) (denoted special sites). Thus, \(x=y=z\) only results in 32 sets of atom coordinates. The 192 general sites are obtained by adding face centered coordinates to the 48 atom coordinates listed in the first group of coordinate sets in Figure xx--CrossReference--fig:ITpage_old--xx. The fact that the space group is face centered is indicated both by the F in the space group name and the four coordinates (0,0,0; 0,1/2,1/2; 1/2,0,1/2; 1/2,1/2,0)+ written just above the general site coordinates in Figure xx--CrossReference--fig:ITpage_old--xx. In the following we use \(N_G\) for the total number of positions at the general site and \(N_S\) for the total number of positions at a special site in a given space group.
In addition to the number of site atoms and coordinates, the second and third columns list a letter label and the point symmetry of the site. The letter label is assigned in alphabetical order where the site with the smallest number of site atoms is named "a". Hence, the special sites \(x=y=z\) and \(x=y=z=0\) and the general sites are named (\(32f\)), (\(4a\)), and (\(192l\)), respectively. The rightmost column contains information about space group or site imposed conditions for having non-zero structure factors. For the example in Figure xx--CrossReference--fig:ITpage_old--xx, the Miller indices for the space group allowed reflections must obey cyclic permutations of \(h+k=2n\) for general \((h,k,l)\); \(l+h=2n\) for \((h,h,l)\) and \(k,l = 2n\) for \((0,k,l)\). Additional rules apply for contributions to the structure factors from atoms at the special sites at (\(48g\)), (\(24d\)) and (\(8c\)).
In modern crystallography programs just one site position per atom type is needed as input because the remaining atoms are generated by the space group symmetry interactions included in the programs. The variables \((x,y,z)\) in general or special sites are replaced by numbers when calculating structure factors and intensities in programs like FullProf (refinable numbers) and Crystallographica (fixed numbers).
Occupancy
From the description above we can see that there is a maximum number of atoms at each site position in a crystal structure (element or isotope). For example, the maximum is 32 atoms of type "\(i\)" at the \(f\)-sites of space group #225 (see Figure xx--CrossReference--fig:ITpage_old--xx). However, some of the atom sites may be empty (vacancies) or partly occupied by different elements (an alloy) or isotopes. The most obvious way to define the occupancy, \(oc_{i,j}\) of a particular atom of type \((i,j)\) is to set it equal to one if all site positions are occupied by the same type of atoms and less than one for sites occupied by vacancies, different elements or isotopes which is equivalent to defining occupancy as the ratio between the total number of atoms in the unit cell at a given site and the site multiplicity of that site.
In the examples described in the section How to use the information in IT (Figure xx--CrossReference--fig:ITpage2--xx and Figure xx--CrossReference--fig:ITpage--xx), some of the oxygen sites are only partly occupied. If all sites in either compound were fully occupied, the chemical formula would be YBa\(_2\)Cu\(_3\)O\(_8\), and the number of formula units within the unit cell would be \(Z = 1\). Hence, according to the above definition of occupancy, \(oc = 1\) for all atoms. However, not all sites are fully occupied for the compounds described in the section How to use the information in IT.
In tetragonal YBa\(_2\)Cu\(_3\)O\(_{6+x}\) the \(2g\)- and \(4i\)-oxygen sites are fully occupied while the \(2f\)-oxygen site contain the excess oxygens. Therefore, the total number of \(2f\)-atoms in the tetragonal unit cell is \(Zx\) and the occupancy \(oc^{C}_{2f} = Zx/2\) because the site multiplicity of the \(2f\)-site is \(N_S=2\). In orthorhombic YBa\(_2\)Cu\(_3\)O\(_{7-x}\) either the \(1b\)-, \(1e\)- or both of these oxygen sites may be oxygen deficient while all other sites are fully occupied. If we assume that the \(1-x\) excess oxygen atoms are distributed between \(1-x-y\) atoms at \(1e\)-sites and \(y\) atom at \(1b\)-sites with site multiplicity \(N_S=1\), i.e. the corresponding occupancies will be \(oc^{C}_{1e} = Z(1-x-y)\) and \(oc^{C}_{1b} = Zy\).
For the examples above the ideal chemical formula represent structures with one formula unit per unit cell, but quite often this is not the case. One example could be Pr\(_{2-x}\)Ca\(_x\)CuO\(_4\) where the chemical formula has been reduced to represent one formula unit which must be repeated four times in order to represent all atoms in the unit cell, i.e. \(Z = 4\). The Pr- and Ca-atoms share the \(8f\)-site positions, and hence the chemical formula representing all atoms in the unit cell is Pr\(_{8-4x}\)Ca\(_{4x}\)Cu\(_4\)O\(_{16}\). Therefore the occupancies of the \(8f\)-Pr and -Ca atoms are \(oc^{C}_{Pr} = Z(2-x)/N_S\) and \(oc^{C}_{Ca} = Zx/N_S\) (\(N_S=8\)), respectively. The occupancies (\(oc^{C}_{i}\)) of the fully occupied Cu-site and the two different O-sites are all 1. This relatively simple way of assigning occupancies is used in e.g. Crystallographica (Cgraf), Powdercell (PCW) and many other programs which calculate structure factors and intensities of diffraction peaks.
In the refinement program FullProf the occupancies can be defined by the site multiplicity scaled by the concentration of the particular atom as given by the chemical formula, e.g. for fully occupied sites \(oc^{FS}_{i}=N_S\). This method is appropriate when refining single phase diffraction patterns, e.g. diffraction patterns without impurities. For multi-phase diffraction patterns this will generally result in incorrect scaling of intensities from the different phases and give erroneous estimates of phase contents. In order to ensure correct scaling of intensities between compounds when using FullProf for refining multi-phase diffraction patterns, the occupancies \(oc^{FS}_{i}\) for each compound must be scaled by the site multiplicity for the general site (\(N_G\)) of the compounds, e.g. \(oc^{FM}_{i} = oc^{FS}_{i}/N_G\). With these definitions, the occupancy for the \(2f\)-oxygen atoms in YBa\(_2\)Cu\(_3\)O\(_{6+x}\) is either \(oc^{FS}_{2f} = xN_S\) or \(oc^{FM}_{2f}=xN_S/N_G\) where \(N_G = 16\). Similarly, the occupancies for the \(1e\)- and \(1b\)-oxygen atoms in YBa\(_2\)Cu\(_3\)O\(_{7-x}\) is either \(oc^{FS}_{1e} = (1-x-y)N_s\) and \(oc^{FS}_{1b} = y N_S\) or \(oc^{FM}_{1e} = (1-x-y)N_s/N_G\) and \(oc^{FM}_{1b} = yN_S/N_G\) where \(N_G = 8\). However, it is strongly recommended to use the latter definition for occupancies even when refining single phase diffraction patterns.
- ↑ International Union of Crystallography, C. Giacovazzo (ed.), Fundamentals of Crystallography (Oxford University Press, 1992)
- ↑ Ashcroft and N.D. Mermin, Solid State Physics (Saunders, 1976)
- ↑ 3.0 3.1 3.2 3.3 3.4 International Union of Crystallography, Theo Hahn (ed.), International Tables for Crystallography, Volume A: Space-group symmetry (D. Reidel Publishing Company, Holland, 1987)
- ↑ 4.0 4.1 International Union of Crystallography, N. F. M. Henry and K. Lonsdale (eds.), International Tables for X-Ray Crystallography, Volume I Symmetry Groups (The Kynoch Press, Birmingham, UK, 1965)
- ↑ CSIS homepage, http://www.xtal.iqft.csic.es/Cristalografia/parte_03-en.html, December 2015.