Magnetic diffraction
We here present the magnetic scattering cross section for diffraction and show a few important examples.
The magnetic diffraction cross section
We will now consider the part of the magnetic scattering cross section in equation this equation from the Scattering_of_neutrons_from_magnetic_ions page, that is purely elastic in both the nuclear and the magnetic system. Hence, the energy \(\delta\)-function falls out and the completeness sum, \(\sum_f |\lambda_{\rm f}\rangle \langle \lambda_{\rm f}| = 1\), can be performed. We now obtain:
\begin{align} \label{eq:magnetic_diffraction0} \left.\frac{d\sigma}{d\Omega}\right|_{\rm magn. el.} &= \left(\gamma r_0 \right)^2 \left[ \frac{g}{2} F(q)\right]^2 \exp(-2W) \sum_{\alpha \beta} \left( \delta_{\alpha\beta}-\hat{q}_\alpha\hat{q}_\beta\right) \\ &\quad \times \sum_{\lambda_{\rm i}} p_{\lambda_{\rm i}} \sum_{j,j'} \exp(i {\bf q} \cdot ({\bf r}_{j'}-{\bf r}_{j})) \big\langle \lambda_{\rm i}| {\bf s}_{j}^\alpha {\bf s}_{j'}^\beta \big| \lambda_{\rm i}\big\rangle , \nonumber \end{align}
which for a static magnetic structure can be simplified to
\begin{align} \label{eq:magnetic_diffraction1a} \left.\frac{d\sigma}{d\Omega}\right|_{\rm magn. el.} = \left(\gamma r_0 \right)^2 \left[ \frac{g}{2} F(q)\right]^2 \exp(-2W) \biggr| \sum_{j} \exp(-i {\bf q} \cdot {\bf r}_{j}) \left\langle {\bf s}_{j,\perp} \right\rangle \biggr|^2 , \end{align}
where \(\langle \, \rangle\) here denotes thermal average and \({\bf s}_\perp\) is the spin component perpendicular to \({\bf q}\).
Equation \eqref{eq:magnetic_diffraction1a} plays the same pivotal role for magnetic diffraction as this equation from the The total cross section for a system of particles page, \(\dfrac{d\sigma}{d\Omega}\biggr|_{\rm coh} = \biggr|\displaystyle\sum_j b_j \exp(i \mathbf q \cdot {\mathbf r}_j)\biggr|^2 \), does for nuclear diffraction.
Paramagnetic scattering
A paramagnet is a collection of magnetic spins, where there is no correlation between different spins, i.e.
\begin{equation} \left\langle {\bf s}_j \cdot {\bf s}_{j'} \right\rangle = 0. \end{equation}
The scattering from a paramagnet is rather simple, since each spin scatters independently of the neighbouring spins. In fact, this is a magnetic version of incoherent scattering. In \eqref{eq:magnetic_diffraction0}, second line, only terms with identical position indices, of the type \({\bf s}_j \cdot {\bf s}_j\), contribute to the double sum. Hence, the dependence of \({\bf q}\) disappears. The five-fold sum can then be replaced with \(2 N s(s+1)/3\), where \(N\) is the number of spins, and the factor 2/3 comes from the fact that two out of three spin components are perpendicular to \(\bf q\). Hence, the result reads:
\begin{equation} \label{eq:paramagnetic_diffraction} \left.\frac{d\sigma}{d\Omega}\right|_{\rm paramagn. el.} = \frac{2}{3} N \left(\gamma r_0 \right)^2 \left[ \frac{g}{2} F(q)\right]^2 \exp(-2W) s (s+1). \end{equation}
Scattering from magnetically ordered structures
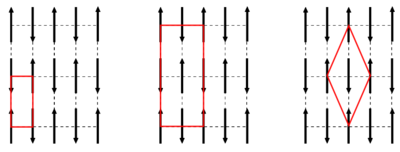
We will here investigate the magnetic scattering from ordered magnetic structures, as described in the section Magnetism in materials. We assume the atoms to be located on an ordered lattice, as described on the Diffraction from crystals page. It should be noted that the magnetic unit cell used to describe ferri- and antiferromagnetically ordered structures is often larger than the structural unit cell. This is illustrated in Figure xx--CrossReference--fig:magnetic_unit_cell--xx.
We now develop the expression for magnetic diffraction in ordered structures, where we in analogy to nuclear diffraction utilize that the magnetic system can be described by repeated unit cells. Eq. (\ref{eq:magnetic_diffraction1a}) then becomes
\begin{align} \left.\frac{d\sigma}{d\Omega}\right|_{\rm magn. el.} = \left(\gamma r_0 \right)^2 \left[ \frac{g}{2} F(q)\right]^2 \exp(-2W) \biggr| \sum_{i,j} \exp(-i {\bf q} \cdot {\bf r}_{j}) \exp(-i {\bf q} \cdot {\bf \Delta}_{i}) \left\langle {\bf s}_{i,\perp} \right\rangle \biggr|^2 \, \end{align}
In analogy to the expressions for nuclear diffraction, the lattice sum over \(j\) produces delta functions, while the sum over the magnetic unit cell (\(i\)) gives what is known as the magnetic structure factor:
\begin{equation} \label{eq:magnetic_SF} F_{\rm M}({\bf q}) = \sum_{i} \exp(-i {\bf q} \cdot {\bf \Delta}_{i}) \left\langle {\bf s}_{i,\perp} \right\rangle . \end{equation} With this, the magnetic scattering cross section from an ordered structure ends up being
\begin{align} \label{eq:magnetic_diffraction2} \left.\frac{d\sigma}{d\Omega}\right|_{\rm magn. el.} &= \left(\gamma r_0 \right)^2 \left[ \frac{g}{2} F(q)\right]^2 \exp(-2W) \\ \nonumber &\quad\times \frac{N (2\pi)^3}{V_0} |F_{\rm M}({\bf q})|^2 \sum_{\boldsymbol\tau} \delta({\bf q}-\boldsymbol\tau-{\bf Q}) , \end{align}
where \({\bf Q}\) is the ordering vector of the magnetic structure, equations (\ref{eq:magnetic_diffraction2}) and (\ref{eq:magnetic_SF}) are equivalent to equation the equation for nuclear diffraction if we make the replacement
\begin{equation} b_j \longrightarrow \gamma r_0 \frac{g}{2} F(q) {\bf s}_{i,\perp} . \end{equation}
The magnitude of this magnetic scattering length is similar to the nuclear scattering lengths, since \(\gamma r_0 = 5.39\) fm and \(g F(q) s/2\) is of the order unity. Hence, the magnetic and nuclear scattering cross sections have similar magnitudes. For large values of S, e.g. in some transition metal salts, like Fe-oxides, or in most rare-earth compounds, the magnetic scattering can completely dominate the diffraction patterns.
In conclusion, magnetic diffraction is seen when the scattering vector equals a magnetic ordering vector (modulo a reciprocal lattice vector), and the intensity of the scattering is proportional to the square of the ordered moment and of similar magnitude as nuclear scattering. Hence, neutron scattering is a clearcut way to determine magnetic structures. Further, it is very useful for the determination of the ordered moments, especially for antiferromagnets where bulk techniques cannot determine the size of the moments.
Example
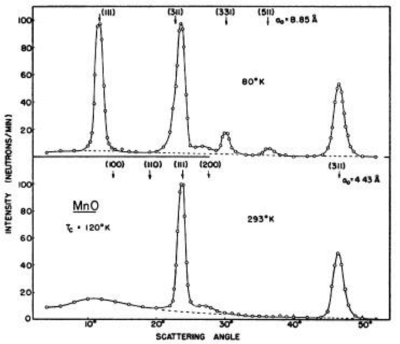
The existence of ordered antiferromagnets was predicted during the 1930'ies and 1940'ies, but the final proof was given by one of the first neutron diffraction experiments by C. Shull in Brookhaven, published already in 1951[1]. For this, and for the invention of neutron diffraction in the first place, C. Shull was awarded the Nobel prize in 1994. Some original data, showing the proof of antiferromagnetism in MnO, are shown in Figure xx--CrossReference--fig:shull--xx.