Problem:Fourier transform
Mathematically the scattering amplitude is the Fourier transform of the distribution of scattering centers (nuclei, electrons, spins) within the material. The scattered intensity (the scattering function) is the square of the scattering amplitude.
The Fourier transform of a function \(\rho(r)\) is written as
- \( F(q) = \displaystyle\int \rho(r) \exp{(iqr)} dr , \)
where \(\rho(r)\) is the function in real space given by positions \(r\), and \(q\) is a coordinate in Fourier space (which in scattering terms usually is called "reciprocal space"). \(\rho(r)\) is in case of scattering theory the position sensitive scattering length density within the sample.
We will consider a one-dimensional space, i.e. all particles (scattering centers) are positioned on a line, and correspondingly only calculate the one-dimensional Fourier transform. We assume further that all particles are points (size = 0).
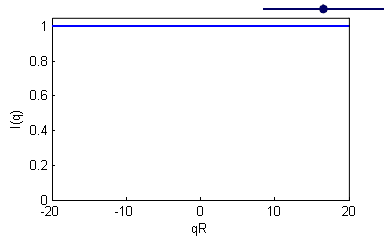
Question 1
Calculate the Fourier transform and the scattering intensity of a sample with only one particle, and plot the normalized scattered intensity \(I(q)=|F(q)|^2/N^2\) versus \(qR\).
A point-particle may mathematically be described as a Dirac \(\delta\)-function with the property
- \( \displaystyle\int \delta(r_0) f(r) d r = f(r_0) .\)
Place the particle in origo \((0,0)\).
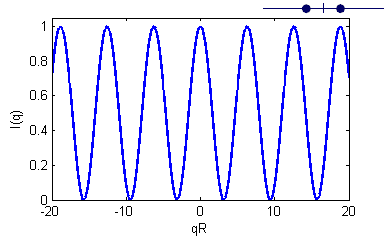
Question 2
Calculate the Fourier transform and the scattering intensity of a one-dimensional crystal with two particles separated with a distance \(R\), and plot the normalized scattered intensity \(I(q)\) versus \(qR\).
Place the particles symmetric around origo, i.e. in \(-R/2\) and \(+R/2\).
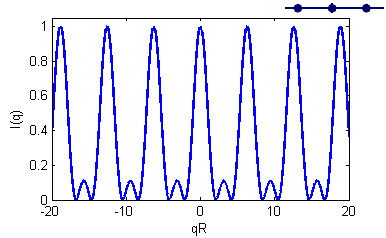
Question 3
Calculate the Fourier transform and the scattering intensity of a one-dimensional crystal with three particles separated with a distance \(R\), and plot the normalized scattered intensity \(I(q)\) versus \(qR\).
Place the particles in origo and in \(-R\) and \(+R\).
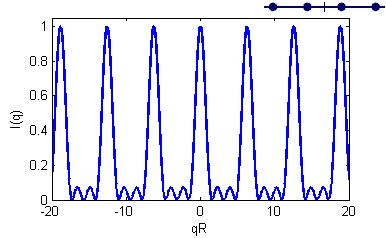
Question 4
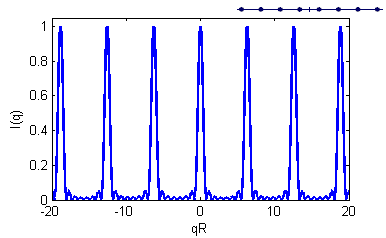
Calculate the Fourier transform and the scattering intensity of a one-dimensional crystal with more particles (4, 5, 6, or ...) separated with a distance \(R\), and plot the normalized scattered intensity \(I(q)\) versus \(qR\).
Place the particles symmetric with respect to origo.
Question 5
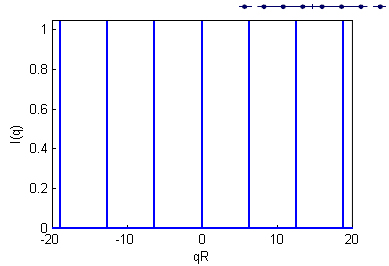
Sketch the normalized scattering intensity of a one-dimensional sample of a very large number of particles (\(\sim\)infinite) separated with a distance \(R\).