Wave description of nuclear scattering
In this section, we discuss the basics of scattering of (neutron) waves, from a semi-classical point of view.
The neutron wave
The incoming (or initial) neutron can be described as a (complex) plane wave
\begin{equation}\label{eq:initialwave} \psi_{\rm i}({\mathbf r}) = \dfrac{1}{\sqrt{Y}} \exp(i {\mathbf k}_{\rm i} \cdot {\mathbf r}) , \end{equation}
where \(Y\) is a normalization constant, implying that the density of the incoming neutron wave is \(|\psi_{\rm i}|^2=1/Y\). This has no implication on the final results, since \(Y\) will eventually cancel in the final equations, but we keep the normalization for completeness. We have in \eqref{eq:initialwave} omitted an explicit time dependence, \(\exp(-i\omega t)\), which plays no role until we discuss inelastic scattering in part IV.
From the equation defining the wavenumber \(\bf k\) on the page Introduction to neutron scattering, the velocity of a neutron described by a plane wave is
\begin{equation}\label{eq:neutron_v} v= \dfrac{\hbar k_{\rm i}}{ m_{\rm n} }. \end{equation}
Similarly, the corresponding incoming neutron flux is
\begin{equation}\label{eq:flux_plane} \Psi_{\rm i} = |\psi_{\rm i}|^2 v = \dfrac{1}{Y} \dfrac{\hbar k_{\rm i}}{m_{\rm n}} . \end{equation}
We will use this result as a stepping stone in the following calculations.
Elastic neutron scattering from a single nucleus
We consider the idealized situation where a neutron with a well defined velocity is scattered by a single nucleus, labeled \(j\), which is (somehow) fixed in position. The scattered neutron can be described as a spherical wave leaving the nucleus, which is centered at \({\bf r}_j\), as shown in Figure xx--CrossReference--fig:1nucleus--xx. The scattered, or final, wave reads:
\begin{equation}\label{eq:scatter_wave} \psi_{\rm f}({\mathbf r}) = \psi_{\rm i}({\mathbf r}_j) \dfrac{-b_j}{|{\mathbf r}-{\mathbf r}_j|} \exp(i k_{\rm f} |{\mathbf r}-{\mathbf r}_j|), \end{equation}
where \(b_j\) is a quantity characteristic for the particular isotope. Since \(b_j\) has the unit of length, it is usually denoted scattering length and is typically of the order 1-10 fm. This above equation is valid only "far" from the nucleus, i.e. for \(|{\bf r}-{\bf r}_j| \gg b_j\). The minus sign in equation \eqref{eq:scatter_wave} is a convention chosen so that most nuclei will have a positive value of \(b_j\).

In experiments, \(r\) is typically of the order 1 m. For convenience, we will position the Origo close to the centre of the "relevant" part of the sample. Hence, the nuclear coordinate, \(r_j\), is typically of the order 1 mm or less, and the density of outgoing neutrons can be approximated by \(|\psi_{\rm f}|^2 \approx b_j^2/(Y r^2)\), omitting \({\bf r}_j\) in the denominator of \eqref{eq:scatter_wave}. The number of neutrons per second intersecting a small surface, \(dA\), is \(v |\psi_{\rm f}|^2 dA = v b_j^2/(Yr^2) dA\). Using equation \eqref{eq:neutron_v} and the expression for solid angle \(d\Omega = dA/r^2\), we reach
\begin{equation}\label{dummy854759296} {\rm number\; of\; neutrons\; per\; second\; in\;} d\Omega = \dfrac{1}{Y} \dfrac{b_j^2 \hbar k_{\rm f}}{m_{\rm n}} d\Omega. \end{equation}
Since the scattering nucleus is fixed, energy conservation requires that the energy of the neutron is unchanged. In this so-called elastic scattering, we therefore have \(k_{\rm i} = k_{\rm f}\). Using equation \eqref{eq:dscs} and \eqref{eq:flux_plane}, this leads to the simple expression for the differential cross section for one nucleus:
\begin{equation}\label{eq:nuclear_diff_cross} \dfrac{d\sigma}{d\Omega} = b_j^2 , \end{equation}
giving the total scattering cross section of
\begin{equation}\label{eq:nuclear_cross} \sigma = 4 \pi b_j^2 . \end{equation}
Scattering from two nuclei - interference
In the field of neutron scattering from materials, we are concerned with the effect of scattering from a system of particles, instead of just one. We therefore begin to add complexity by considering the scattering from two nuclei, again placed at fixed positions. This simple system will reveal some very important features, which we will utilize later.
The neutron wave that is scattered from the two nuclei is in fact describing just one single neutron. Nevertheless, this neutron "senses" the presence of both nuclei, meaning that the wave amplitude scattered from one nucleus will add to the wave amplitude scattered from another nucleus. This interference is a central aspect in most scattering techniques.
We assume that the incoming neutron wave at the position of the second nucleus is not notably attenuated by the scattering of the first nucleus, and vice versa. This is known as the Born Approximation.
Let us describe the situation in more precise terms. We assume elastic scattering, \(k_{\rm i} = k_{\rm f} \equiv k\) and we denote the nuclear scattering lengths as \(b_j\) and \(b_{j'}\), respectively. Generalizing equation \eqref{eq:scatter_wave}, the outgoing (final) wave can be described as
\begin{equation}\label{dummy566330241} \psi_{\rm f}({\mathbf r}) = - \left( b_j \dfrac{\psi_{\rm i}({\mathbf r}_j)}{|{\mathbf r}-{\mathbf r}_j|} \exp(i k_f |{\mathbf r}-{\mathbf r}_j|) + b_{j'} \dfrac{\psi_{\rm i}({\mathbf r}_{j'})}{|{\mathbf r}-{\mathbf r}_{j'}|} \exp(i k_f |{\mathbf r}-{\mathbf r}_{j'}|) \right) , \end{equation}
where \(\psi_{\rm i}({\bf r})\) is the plane wave given by equation \eqref{eq:initialwave}. The two nuclei are assumed to be closely spaced compared with the distance to the observer: \(|{\bf r}_j - {\bf r}_{j'}| \ll r\). Choosing the origin to lie close to the two particles, the denominators can be considered equal, giving
\begin{equation}\label{eq:interference1} \psi_{\rm f}({\mathbf r}) = - \dfrac{1}{\sqrt{Y}} \dfrac{1}{r}\big[ b_j \exp(i {\mathbf k}_{\rm i}\cdot {\mathbf r}_j) \exp(i k_f |{\mathbf r}-{\mathbf r}_j|) + b_{j'} \exp(i {\mathbf k}_{\rm i}\cdot {\mathbf r}_{j'}) \exp(i k_f |{\mathbf r}-{\mathbf r}_{j'}|) \big] \end{equation}
In contrast to the "sloppy" treatment of the distance \(r\), we need to very accurately keep track of the length \(|{\bf r}-{\bf r}_j|\), since it enters in the phase of the complex wave function. It is convenient to write the nuclear coordinate, \({\bf r}_j\), as the sum of a component parallel to and a component perpendicular to \({\bf r}\):
\begin{equation}\label{dummy801871315} |{\mathbf r}-{\mathbf r}_j| = |{\mathbf r}-{\mathbf r}_{j,||}-{\mathbf r}_{j,\perp}| = \sqrt{\left|{\mathbf r}-{\mathbf r}_{j,||}\right|^2+\left|{\mathbf r}_{j,\perp}\right|^2} , \end{equation}
where the last step is due to Pythagoras. The last term in the square root is by far the smallest and vanishes to first order. To check the order of magnitude of the second order correction, we take a "large" distance between nuclei of \(|r_j| \approx 1\,\mu\)m and \(|{\bf r}-{\bf r}_{j,||}| \approx 1\) m. This gives an error in the approximation of \(\approx 0.005\) Å; much smaller than the typical neutron wavelength we consider. This means that effectively only one nuclear coordinate, \({\bf r}_{j,||}\), contributes and that the square root can be lifted to give \(|{\bf r}-{\bf r}_j|=|{\bf r}-{\bf r}_{j,||}|\). Now, we can write
\begin{equation}\label{eq:scalar_to_dot} k_f |{\mathbf r} - {\mathbf r}_{j,||}| = {\mathbf k}_{\rm f} \cdot ({\mathbf r} - {\mathbf r}_{j,||}), \end{equation}
where \({\bf k}_{\rm f}\) is a wave vector with length \(k_{\rm f}\) (which here equals \(k\)), oriented parallel to \({\bf r}\). Since \({\bf k}_{\rm f} \cdot {\bf r}_{j,\perp} = 0\), we have \({\bf k}_{\rm f} \cdot {\bf r}_{\rm j,||} = {\bf k}_{\rm f} \cdot {\bf r}_{\rm j}\). We insert this in the right side of \eqref{eq:scalar_to_dot} and take the complex exponential, reaching
\begin{equation}\label{dummy1462842445} \exp(i k_f |{\mathbf r}-{\mathbf r}_j|) = \exp(i {\mathbf k}_{\rm f} \cdot ({\mathbf r}-{\mathbf r}_j)). \end{equation}
Rearranging terms, the final wave can be written as
\begin{equation}\label{dummy906628448} \psi_{\rm f}({\mathbf r}) = -\dfrac{1}{\sqrt{Y}} \dfrac{1}{r}\exp(i{\mathbf k}_{\rm f}\cdot{\mathbf r}) \left[ b_j \exp(i ({\mathbf k}_{\rm i}-{\mathbf k}_{\rm f})\cdot {\mathbf r}_j) + b_{j'} \exp(i ({\mathbf k}_{\rm i}-{\mathbf k}_{\rm f})\cdot {\mathbf r}_{j'}) \right] . \end{equation}
This shows that the observer at position \({\bf r}\) will experience a scattered neutron wave that locally seems like a plane wave with wavevector that is parallel to ${\bf r}$.
The intensity of neutrons impinging on a small area is again given as \(v |\psi_{\rm f}({\bf r})|^2 dA\). Hereby we can write the scattering intensity as
\begin{equation}\label{dummy1518846130} {\rm number\; of\; neutrons\; per\; second\; in\;} d\Omega = \dfrac{1}{Y} \dfrac{\hbar k_{\rm f}}{m_{\rm n}} d\Omega \left| b_j \exp(i \mathbf{q} \cdot {\mathbf r}_j) + b_{j'} \exp(i \mathbf{q} \cdot {\mathbf r}_{j'}) \right|^2 , \end{equation}
where we have defined the very central concept of neutron scattering, the scattering vector, as
\begin{equation}\label{dummy903425712} \mathbf{q} = {\mathbf k}_{\rm i} - {\mathbf k}_{\rm f} . \end{equation}
The final expression for the differential scattering cross section for elastic scattering from nuclei now becomes:
\begin{equation}\label{eq:interference2} \dfrac{d\sigma}{d\Omega} = b^2 \big|\exp(i \mathbf{q} \cdot {\mathbf r}_j) +\exp(i \mathbf{q} \cdot {\mathbf r}_{j'})\big|^2 = 2 b^2 \big( 1 + \cos[\mathbf{q} \cdot ({\mathbf r}_j-{\mathbf r}_{j'})] \big) . \end{equation}
At some values of \(\mathbf{q}\), we have \(\cos[\mathbf{q} \cdot ({\bf r}_j-{\bf r}_{j'})] = -1\), meaning that the waves from the two nuclei are in counter phase and that the cross section thus vanishes. At other values of \(\mathbf{q}\), the scattering is in phase, \(\cos[\mathbf{q} \cdot ({\bf r}_j-{\bf r}_{j'})] = 1\), giving a value of the cross section of \(4b^2\), which is four times the cross section of a single nucleus (\(b^2\)). This enhancement of the signal is the essence of interference.
Coherent elastic scattering from a system of nuclei
In neutron scattering, we deal with interference between waves scattered from a large number of nuclei in the same way as we have seen for two nuclei above. Fortunately, the principle of interference applies equally well to many particles as to two. For this reason, we can simply generalize equation (\ref{eq:interference2}) to contain several particles \begin{equation} \label{eq:diffraction} %Squires never writes this - strange! \left.\frac{d\sigma}{d\Omega}\right|_{\rm coh} = \biggr|\sum_j b_j \exp(i {\bf q} \cdot {\bf r}_j)\biggr|^2 \, . \end{equation} This is a very important result, which is used in most types of neutron scattering.
Experimental considerations
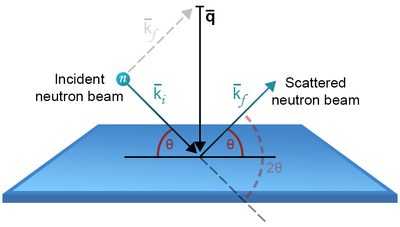
In a scattering experiment, one will always measure the scattering angle with respect to the incoming beam, as illustrated in Figure xx--CrossReference--fig:theta_2theta--xx. The scattering angle is known as \(2\theta\). In elastic scattering, \(k_{\rm i}=k_{\rm f} \equiv k\), and we can see from the figure that
\begin{equation} \label{eq:Bragg_ktoq} %(S3.51) q = 2 k \sin(\theta) \, \end{equation}
or the often presented alternative
\begin{equation} \label{eq:Bragg_lambdatoq} q = 4 \pi \sin(\theta) / \lambda \, . \end{equation}