Problem:Selection of materials for neutron scattering experiments
Most nuclei scatter neutrons incoherently, i.e. in random directions. Further, some nuclear isotopes are able to absorb neutrons by nuclear processes. We will now take a closer look at these properties for various materials.
Question 1
Consider the incoherent scattering cross section \(\sigma_{\text{inc}}\) for the typical elements occuring in organic materials: H, C, N, O and P. Suggest a method to reduce the incoherent background from organic samples?
One can reduce the incoherent background from organic materials by subtitution of H with D.
Question 2
Some transition metals (Sc \(\rightarrow\) Zn) display a strong incoherent scattering, and one of them is used as a standard incoherent scatterer (for calibration purposes). Try to figure out which one it is.
Vanadium (V) has small coherent scattering length \(b\) and small absorption cross-section \(\sigma_a\), but large incoherent cross-section \(\sigma_\text{inc}\).
Question 3
Sometimes other, more easily accessible, materials are used as incoherent scatterers instead. Suggest one.
Other (cheaper) incoherent scatterers could be anything with H, e.g. plastic and the like.
Question 4
Which metals may be used for neutron shielding? Calculate the penetration depth \(1/\mu\) in these materials for neutron energies of 5 meV. Assume that the number density of atoms in the metals is 1/(16 Å\(^3\)).
The penetration depth is defined as the depth \(z'\) where \(I(z')/I_0=e^{-1}\). The energy of a 'standard thermal neutron' is \(E^{\rm th} = 25 \) meV.
Neutron shielding is made from material with large absorption cross-section \(\sigma_a\). An example could be Cd or even better Gd. Since the coherent scattering cross-section is very small in comparison to the absorption cross-section in these materials, the attenuation is mostly due to absorption. Hence the attenuation coefficient is \(\mu\approx\mu_a=n\sigma_a\), where \(n\) is the number density of atoms in the metal with absorption cross-section \(\sigma_a\). The intensity as a function of depth \(z\) in the material is \(I(z)=I_0 e^{-\mu z}\), and hence the penetration depth (defined as the depth \(z'\) where \(I(z')/I_0=e^{-1}\)) is \(1/\mu = 1/(n\sigma_a)\).
- \(\sigma_a^{5 {\rm meV}} = \sigma_a^{\rm th}\sqrt{\dfrac{E^{\rm th}}{5 {\rm meV}}}= \sigma_a^{\rm th}\sqrt{5} ,\)
and hence
- \( \mu^{5{\rm meV}} = \mu^{\rm th}\sqrt{\dfrac{E^{\rm th}}{5{\rm meV}}}= \mu^{\rm th}\sqrt{5} .\)
So with \(n=1/(16\)Å\({}^3)=6.25\cdot10^{28}\text{m}^{-3}\), \(\sigma^{\text{5meV}}_{\rm Cd}=5635\cdot 10^{-28}\text{m}^2\), giving \(1 /\mu_{\rm Cd}^{5 \text{meV}}=0.03\text{mm}\). For Gd, using the same density \(n\), the absorption cross-section is \(\sigma^{\text{5meV}}_{\rm Cd}=11113\cdot 10^{-28}\text{m}^2\) giving \(1 / \mu_\text{Gd}^\text{5meV} = 1 ~\mu\text{m}\).
Question 5
Also boron nitride, BN, (\(V_0 = 11.81\) Å\(^3\)) is used for shielding purposes. This material is used e.g. to make adjustable diaphragms (slits) to control the size of the neutron beam. Calculate the thickness of BN needed to reach an attenuation factor of \(10^{-6}\) (that is, only a fraction of \(10^{-6}\) of the neutrons in the beam are left in the beam at this thickness) for 5 meV neutrons. What will the attenuation then be for neutrons of 20 meV and 180 meV?
The attenuation coefficient for BN at 25 meV is
- \(\mu^{25{\rm meV}} = \displaystyle\sum_i \dfrac{N_i\sigma_i}{V_0}=\dfrac{(767+1.90)\cdot 10^{-28}{\rm m}^2}{11.81\cdot 10^{-30}{\rm m}^3}= 6511 {\rm m}^{-1} ,\)
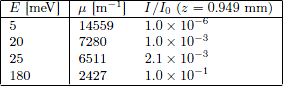
from which \(\mu^{5\text{meV}}=\mu^{25\text{meV}}\sqrt{5}=14559\text{ m}^{-1}\). Other attenuation coefficients for BN are shown in Table xx--CrossReference--tab:BNtransmission--xx.
To get the neutron beam intensity attenuated by a factor of \(10^{-6}\):
- \(\dfrac{I(z)}{I_0}= 10^{-6}= e^{-\mu\cdot z} \quad\Rightarrow\quad z = -\dfrac{\text{ln}{10^{-6}}}{\mu} ,\)
I.e. \(z^{5\text{meV}}= 0.949~\text{mm}\) and \(z^{20\text{meV}}= 1.90 ~\text{mm}\). The higher the energy of the neutrons the thicker BN is needed to attenuate them to a specified fraction. For a specific thickness of BN more high energy neutrons will be transmitted, as shown in Table xx--CrossReference--tab:BNtransmission--xx.
Question 6
In a neutron scattering experiment, the sample surroundings in the beam must be "clean" in the sense of absorption and (incoherent) scattering. Which metal would you suggest for constructing cryostats for neutron experiments?
Alumininium would be a good material for cryostats since it has small absoption and incoherent scattering cross-sections. Silicon might be even better but is mechanically difficult to work with.