Problem:Hydrogen as a moderator
Show that the energy of a neutron is on average halved by collision with a proton; c.f. the equation on the Neutron sources and moderators page.
Try modelling the scattering as simple mechanical scattering of spheres with momentum and energy conservations.
This problem is easier to solve in only two dimensions (and you loose no generality by doing this, since the collision of two spheres can always be modeled by using only two dimensions, by rotating the coordinate system).
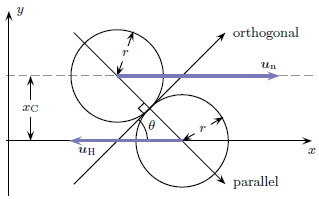
Using the variable names defined in Figure xx--CrossReference--fig:hydrogen-neutron-collision--xx, and naming the velocities after collision \(\mathbf v_\text{n}\) and \(\mathbf v_\text{H}\), respectively, we have momentum conservation
\begin{equation*} m u_{\text{n},p} + m u_{\text{H},p} = m v_{\text{n},p} + m v_{\text{H},p} , \end{equation*}
where the \(p\) stand for the parallel direction. We also have energy conservation
\begin{equation*} \frac{1}{2} m \mathbf u_\text{n}^2 + \frac{1}{2} m \mathbf u_\text{H}^2 = \frac{1}{2} m \mathbf v_\text{n}^2 + \frac{1}{2} m \mathbf v_\text{H}^2 . \end{equation*}
These two equations combine to give the final neutron velocity in (parallel,orthogonal)-coordinates
\begin{equation*} v_\text{n} = \binom{v_{\text{n},p}}{v_{\text{n},o}} = \binom{u_{\text{H},p}}{u_{\text{n},o}} , \end{equation*}
where the \(o\) stand for the orthogonal direction. If the initial energy of the neutron is \(E_\text{i}\), the final neutron energy after the collision, \(E_\text{f}\), can further be found to be
\begin{equation*} E_\text{f} = E_\text{i} \cos^2\theta + E_\text{H} \sin^2\theta , \end{equation*}
where \(E_\text{H}\) is the energy of the hydrogen nucleus before the collision, and where \(\theta -\pi/2 = \sin^{-1}(x_\text{C}/(2r))\) is the rotation angle of the coordinate system.
If a neutron starts out with a higher energy than the energy of the moderator material, here the simple hydrogen nuclei, it will hence never (in this simple case) get an energy below the moderator material nuclei energy, since \(\cos^2\theta + \sin^2\theta = 1\). Assuming an even distribution of \(\theta\), the average of \(\sin^2\theta\) and \(\cos^2\theta\) over \(0<\theta<\pi/2\) is \(1/2\), and the expression for the average energy after the collision can be rewritten as
\begin{equation*} \langle E_\text{f} \rangle = \frac{ \langle E_\text{i} \rangle}{2} + \frac{ \langle E_\text{H} \rangle}{2} = \frac{ \langle E_\text{H} \rangle + \langle E_\text{E} \rangle}{2} + \frac{ \langle E_\text{H} \rangle}{2} = \frac{ \langle E_\text{E} \rangle}{2} + \langle E_\text{H} \rangle , \end{equation*}
where \(E_\text{E}\) is the excess energy \(E_\text{i}-E_\text{H}\). Hence, the neutron will on average converge towards the moderator material energy by half the excess energy at each scattering.