Lattice vibrations, classical treatment
We will here describe lattice vibrations in general. This section deals with the purely classical description, while the section Phonons, quantum mechanical treatment introduces the quantum mechanical treatment.
Dynamical description of nuclei in crystals
Let us as before denote the equilibrium position of the nuclei with \({\bf r}_j\) -- or for a non-Bravais lattice \({\bf r}_j + \boldsymbol\Delta_i \) with \(j\) being the index for the unit cell and \(i\) labeling the atom within the unit cell. These atomic positions are constant in time (assuming that the crystal center-of-mass is at rest). We describe the motion of the nuclei with the (small) displacement vector \({\bf u}_{ij}(t)\). The time-dependent nuclear position now reads
\begin{equation}\label{eq:vibration} {\mathbf R}_{ij}(t) = {\mathbf r}_j + \boldsymbol\Delta_i + {\mathbf u}_{ij}(t) . \end{equation}
We approximate the potential energy between two neighbour atoms by a quadratic form in the difference between their displacements:
\begin{equation}\label{eq:harmonic_potential} V_{jj'} = \dfrac{1}{2} K_{jj'} ({\mathbf u}_{j}(t) - {\mathbf u}_{j'}(t))^2 + V_0, \end{equation}
where \(K_{jj'}\) is the spring constant for the (in this case isotropic) atom-atom interaction, \(V_0\) is a zero point of the energy, and we have dropped the subscripts \(i\) for convenience.
The one-dimensional nearest neighbour model
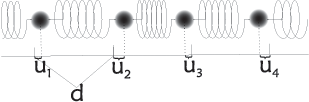
We will now turn to a few concrete one-dimensional examples, which will give much insight in the physics of phonons. We first consider a model of \(N\) identical particles (atoms) of mass \(M\), with equilibrium spacing \(a\), and identical nearest neighbour spring constants \(K\). This system is illustrated in Figure xx--CrossReference--fig:springs--xx. The equilibrium distance between atoms is \(a\), so we can write \(r_j = j a\).
The net spring force between two particles is zero in equilibrium (where all \(u_j=0\)). In the general case, the force on particle \(j\) from particle \(j+1\) reads:
\begin{equation} \label{dummy132847800} F_{j,j+1}(t) = K \left[ - u_j(t) + u_{j+1}(t) \right] , \end{equation}
where \(K\) is the spring constant of one spring. Including also the similar coupling \(F_{j-1,j}(t)\), the equation of motion for \(u_j\) can be written using Newton's second law:
\begin{equation}\label{eq:N2} M \dfrac{d^2}{dt^2} u_j(t) = K \left[ u_{j-1}(t) + u_{j+1}(t) - 2 u_j(t) \right] . \end{equation}
To simplify the calculations, we assume periodic boundary conditions, i.e. we assume that atom 1 is connected with atom \(N\) with a force term equivalent to \(F_{j,j+1}\). The error introduced by this so-called Born-von Karman boundary conditions will vanish in the thermodynamic limit (\(N \rightarrow \infty\)) and hence it is safe for us to make this choice that makes the problem mathematically simple. The periodic boundary conditions are equivalent to defining \(u_{N+1} \equiv u_1\).
We look for solutions to equation \eqref{eq:N2} of the plane wave form
\begin{equation}\label{eq:fourier} u_j(t) = A \exp(i q j a - i \omega_q t) , \, \end{equation}
where the real value of \(u_j(t)\) represent the physical displacement, while the imaginary part contains information on the phase of the vibrations. The amplitude for the vibrations, \(A\), is chosen to be real. The periodic boundary conditions imply that the phase is invariant under a translation of \(N\) atoms. This gives a choice of possible values of the wave vector:
\begin{equation} \label{dummy908100751} q = \dfrac{n}{N} a^* , \end{equation}
where \(n\) is an integer and the reciprocal lattice vector is \(a^* = 2\pi/a\).
Inserting equation \eqref{eq:fourier} into equation \eqref{eq:N2}, we reach
\begin{equation} \label{dummy475684766} -\omega_q^2 M u_j(t) = K u_j(t) \left[ \exp(iqa) + \exp(-iqa) - 2 \right]. \end{equation}
This simplifies directly into the dispersion relation we are looking for
\begin{equation}\label{eq:dispersion_1atom} \omega_q^2 = 2 \omega_0^2 \left[ 1- \cos(qa) \right] = 4 \omega_0^2 \sin^2(qa/2). \end{equation}
Here, the characteristic frequency, \(\omega_0\), is defined as the resonance frequency of the related single-particle harmonic oscillator,
\begin{equation}\label{eq:omega0} \omega_0 = \sqrt{\dfrac{K}{M}}. \end{equation}
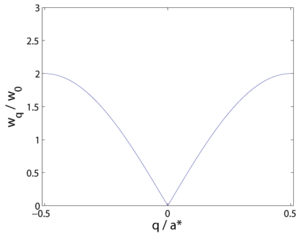
The dispersion relation for one Brillouin zone, \(| {\bf q} | \leq \pi/a = |{\bf a}^*| / 2\), is shown in Figure xx--CrossReference--fig:nn_dispersion--xx. At small \(q\), the dispersion is approximately linear, so it is meaningful to define a velocity of the lattice vibrations as
\begin{equation} \label{dummy1908810697} c = \dfrac{\partial \omega_q}{\partial q} \approx \omega_0 a . \end{equation}
These long-wavelength lattice vibrations are, in fact, the same as sound waves in materials. Therefore, this type of vibrations is known as acoustic.
As we shall see in the section Phonons, quantum mechanical treatment, the quantized lattice vibrations are known as phonons. The low-energy phonons are in analogy with the discussion above denoted acoustic phonons.
Optical lattice vibrations
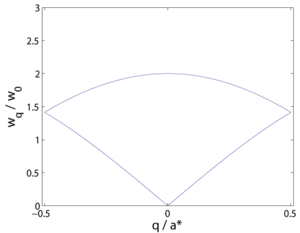
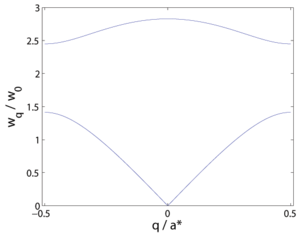
A symmetry breaking in the Bravais crystal can cause a doubling of the unit cell, even if it may have little effect on the vibration physics. This leads to reduction of the Brillouin zone by a factor 2, \(a_2^* = a^*/2\). The vibration modes are now denoted differently. The part of the dispersion relation that has the highest values of \(|q|\) is "folded back" by \(q_2 = q-a_2^*\) to create a second branch of the dispersion relation. This new, most often higher lying, branch is now denoted the optical branch. The optical and acoustic branches are shown in Figure xx--CrossReference--fig:nn_optical--xx.
The optical mode for \(q=0\) is particularly easy to interpret: All unit cells behave identically, while the two atoms in the unit cell vibrate in counter phase. In the original system, Figure xx--CrossReference--fig:nn_dispersion--xx, this corresponds to the zone boundary: \(q = \pi/a\). The frequency at this position is \(\omega_{\pi/a} = 2 \omega_0\).
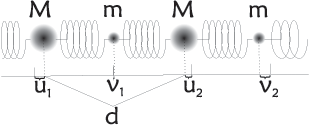
For the sake of self-consistency, let us calculate the above result explicitly. To describe this motion quantitatively, we denote the displacement of the first atom in the \(j\)'th unit cell \(u_j(t)\), while the second atom is denoted \(v_j(t)\). The equation of motion now reads
\begin{align} \label{eq:general2} M \dfrac{d^2}{dt^2} u_j(t) &= K \left[ v_{j-1}(t) + v_j(t) - 2 u_j(t) \right] , \\ M \dfrac{d^2}{dt^2} v_j(t) &= K \left[ u_{j+1}(t) + u_j(t) - 2 v_j(t) \right] .\nonumber \end{align}
Since \(q=0\), the motion is independent of \(j\). Hence, we can reduce the expression to:
\begin{align} \label{eq:optical1} \omega^2 u(t) &= 2 \omega_0^2 \left[ u(t) - v(t) \right] , \\ \omega^2 v(t) &= 2 \omega_0^2 \left[ v(t) - u(t) \right] .\nonumber \end{align}
This is the same equation of motion as for two identical particles connected by one spring with strength \(2K\). When we take into account that the two atoms in the unit cell move in counter phase, we have \(u(t) = - v(t)\), leading to \(\omega = 2 \omega_0\), as we aimed to show.
In general, for a one-dimensional system with \(N\) atoms in the unit cell, there will be 1 acoustic and \(N-1\) optical modes.
One-dimensional models with two different atoms
Let us now treat the one-dimensional system with identical springs of constant \(K\), but two different atoms per unit cell. This is illustrated in Figure xx--CrossReference--fig:springs2--xx.
The masses of the two atoms are denoted \(m\) and \(M\), respectively, with \(M\) the largest of the two. We define
\begin{equation}\label{eq:twoatoms} \beta = \frac{m}{M} < 1 , \end{equation}
and \(\omega_0\) is defined as in equation \eqref{eq:omega0}.
Solving the equations of motion for the two atoms (see Problem: Classical vibrations with a two-atom unit cell), we reach the dispersion relation
\begin{equation}\label{eq:spring2d} \omega_q^2 = 2 \omega_0^2 \left[1-\cos(qa/2) \alpha^{-1} \right] , \end{equation}
where \(\alpha\) is the ratio of vibration amplitudes for the two types of atoms:
\begin{equation} \label{dummy2033491713} \alpha = \dfrac{1-\beta \pm \sqrt{(1-\beta)^2 + 4 \beta\cos^2(qa/2)}}{2\cos(qa/2)} . \end{equation}
Note that for \(q \rightarrow 0\), we have the solutions \(\alpha_1 = 1\) (long-wave acoustic phonons) and \(\alpha_2 = -\beta\); the \(q=0\) optical phonons, where the atoms move in counter phase and the light atoms vibrate with a larger amplitude. The resulting dispersion relation for \(\beta=1/3\) is shown in Figure xx--CrossReference--fig:2atom_dispersion--xx.
*Phonons in three dimensions
The problems has been treated in a number of textbooks, e.g. in Squires, Appendix G[2]. The solution is very similar to the one-dimensional case, except that the phonons now have both a (three-dimensional) \({\bf q}\) and a polarization vector, \({\bf e}_{q,p}\), which represents the direction of the vibration:
\begin{equation} \label{dummy1137015881} {\mathbf u}_j(t) = \sqrt{\dfrac{\hbar}{2 M N}} \displaystyle\sum_{q,p} \dfrac{{\mathbf e}_{q,p}}{\sqrt{\omega_{q,p}}} \left[ a_{q,p} \exp(i({\mathbf q}\cdot {\mathbf r}_j - \omega_{q,p} t)) + a^\dagger_{q,p} \exp(-i({\mathbf q}\cdot {\mathbf r}_j - \omega_{q,p} t)) \right] , \end{equation}
where \(p\) is the polarization index, which runs over 3 times the number of atoms in the unit cell. The Hamiltonian for the phonon system reads
\begin{equation} \label{dummy1572956896} H = \displaystyle\sum_{q,p} \hbar \omega_{q,p} \left( a^\dagger_{q,p} a_{q,p} + \dfrac{1}{2} \right) . \end{equation}
In general, there are two types of phonons:
- Longitudinal: The polarization vector \({\bf e}_{q,p}\) is parallel to \({\bf q}\).
- Transverse: The two polarization vectors \({\bf e}_{q,p}\) are perpendicular to \({\bf q}\). Usually, these modes have lower energies than the longitudinal ones.
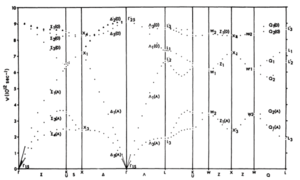
For a non-Bravais lattice with \(m\) atoms per unit cell, there are only 3 acoustic modes. The remaining \(3(m-1)\) are optical modes with a non-zero frequency (often a local maximum) at \(q=0\). A typical set of phonon dispersion curves for a two-atom unit cell (Ge) is presented in Figure xx--CrossReference--fig:phonon--xx.
The role of lattice vibrations in materials
The lattice vibrations determine a number of properties of materials. A straigtforward example is the acoustic properties, where the acoustic phonons are equal to sound waves.
An important consequence of lattice vibrations is the thermodynamic properties of materials. In fact the heat capacity and thermal conductivity in insulating materials stem from the lattice vibrations.
As we shall see in the Phonons, quantum mechanical treatment section, the lattice vibrations quantize in energy units of \(\hbar \omega_q\). These quasiparticles are denoted phonons and are approximately Bosons, i.e. there can be several phonons with the same \({\bf q}\); a larger number of phonons corresponds to larger classical vibration amplitudes. The occupation numbers of phonons are thus given by Bose-Einstein statistics,
\begin{equation} n_{q} = n_{\rm B}(\hbar \omega_q/k_{\rm B}T) . \end{equation}
where \(n_{\rm B}\) is the Bose occupation number
\begin{equation} \label{eq:nB} n_{\rm B}\left(\frac{\hbar\omega}{k_{\rm B}T}\right) = \frac{1}{\exp\left( \dfrac{\hbar\omega}{k_{\rm B}T} \right) - 1} \, . \end{equation}
These equations form, together with knowledge of the dispersion relation, \(\omega_q\), the basis for the description of the thermal properties of phonons, which is elaborated on in many textbooks, e.g. the one by Kittel[1]. Is it therefore essential to measure the phonon dispersion relations in order to understand thermal properties of materials.
Another, and more complex part of phonon science is the study of crystal anharmonicities, caused by 4'th and higher order terms in the atomic potentials. Anharmonicities give rise to e.g. thermal expansion, and can be inferred from studies of phonon lifetimes, which in turn can be found by studying the energy spread in the phonon energies. This is, however, beyond the scope of these notes.
- ↑ C. Kittel. Introduction to Solid State Physics. Wiley, 2004.