Elastic magnetic scattering

Due to its magnetic dipole moment, the neutron can be affected by a variation of the local magnetic field inside materials. This magnetic field most often originates from atomic magnetic moments. To simplify the presentation, we here consider only magnetic fields arising from the spins of electrons in unpaired atomic orbitals.

A more complete treatment of magnetic neutron scattering theory is given in a number of textbooks, e.g.~the one by Marshall and Lovesey.

The study of the orientation of magnetic moments in materials is a rich and diverse field, in which neutron scattering is a key technique. We will in this chapter turn to the study of magnetic structures by magnetic neutron diffraction, while Inelastic magnetic scattering is devoted to the treatment of inelastic magnetic scattering, e.g. from magnetic excitations.

Magnetic scattering can also be performed with spin-polarised neutrons, where additional information on magnetic properties can be obtained. This will be covered by a later version of these notes.

Magnetism in materials

We begin this page with a short description of magnetic properties of materials. We will concentrate on materials where the magnetic moments are localised and interact via simple exchange interactions. We shall see how these interactions lead to a number of different magnetically ordered structures.

There exists a number of textbooks devoted to magnetic properties of materials. For a general introduction to the field, we recommend the fairly recent book by S. Blundell .

We begin with a short description of magnetic properties of materials. We will concentrate on materials where the magnetic moments are localised and interact via simple, so-called exchange interactions. We shall see how these interactions lead to a number of different magnetically ordered structures.

A number of textbooks are devoted to magnetic properties of materials. For a general introduction to the field, we recommend the one by S. Blundell .

Magnetic ions

The magnetic moment of atoms and ions stems from the angular moment of the electrons. The orbital angular moment, \({\bf l}\), generates a circular current, equivalent to that of a tiny coil. This produces a magnetic dipole moment of \begin{equation} {\bf \mu}_l = \mu_{\rm B} {\bf l} , \end{equation} where the Bohr magneton is \begin{equation} \mu_{\rm B} = \frac{\hbar e}{2 m_{\rm e}} = 9.274 \cdot 10^{-24} {\rm J/T} = 5.788 \cdot 10^{-5}\,{\rm eV/T}. \end{equation} For similar reasons, the spin of the electron causes a magnetic dipole moment of \begin{equation} \label{eq:emoment2} {\bf \mu}_s = - g \mu_{\rm B} {\bf s} \, , \end{equation} where \({\bf s}\) is the electron spin and \(g=2.0023\) is the gyromagnetic ratio of the electron, describing a relativistic enhancement of the magnetic moment.

We have above taken \({\bf l}\) and \({\bf s}\) to be unitless (i.e. the actual orbital angular moment is \(\hbar {\bf l}\) and similar for the spin angular moment). We will remain with this definition in all of these notes.

\paragraph{Hund's rules} We will now determine the total angular moment of a free atom or ion. In general, we use the \(z\)-axis as the quantization axis of angular momenta.

A general quantum mechanical result gives us the rather intuitive addition rule of angular momenta .

\begin{equation} {\bf L} = \sum_i {\bf l}_i , \qquad {\bf S} = \sum_i {\bf s}_i , \qquad {\bf J} = {\bf L} + {\bf S} , \end{equation} where \({\bf J}\) is the total angular momentum. The quantum numbers, \(L\), \(S\), and \(J\) take integer or half-integer values. \(J\) will assume a value between \(S+L\) and \(|S-L|\). In general, due to the coupling between the magnetic field from the orbital motion and the spin magnetic moment (the spin-orbit coupling), \(J\) is the only constant of motion.

We immediately note that closed shells represent \(L=S=J=0\), since all positive and negative values of \(l_i^z\) and \(s_i^z\) are represented. Hence, we only need to consider partially filled shells.

Due to electrostatic repulsion between atoms, combined with quantum mechanics (the Pauli principle and the spin-orbit coupling), it is energetically favourable for the electrons to occupy the partially filled shells in a particular way. This is described by Hund's rules (in order of highest priority) :

• Maximize \(S\).
• Maximize \(L\).
• For less-than-half-filled shells: Minimize \(J\).\\ For more-than-half-filled shells: Maximize \(J\).

These rules are, however, only general rules of thumb that may be overruled by other effects, e.g.\ crystal electric fields as discussed below.

\paragraph{Quenching} In materials, the ions cannot be considered free. In stead, they interact with their neighbouring ions through electrostatic forces, also known as crystal electric fields. This implies that the rotational symmetry of the atomic orbitals is broken. In many cases, \({\bf L}\) is then no longer a good quantum number, and the average contribution to the magnetic moment from \({\bf L}\) vanishes, whence \({\bf J} = {\bf S}\). This effect is denoted quenching.

Quenching is seen for ions of most of the transition metals, i.e. the metals with a partially filled 3d shell, which are some of the most prominent magnetic ions in solids. The other prominent group, the rare-earth metals (with partially filled 4f shells), are less prone to quenching due to the relatively smaller spatial extend of the 4f orbitals.

In most of the text to follow, we assume a complete quenching of the magnetic ions, so that the only magnetic degree of freedom is the spin quantum number, \({\bf S}\).

Interactions between magnetic ions

Due to the magnetic moments of ions, described earlier in Magnetism in materials, the ions will interact with an external magnetic field. This is described by the Zeeman Hamiltonian: \begin{equation} \label{eq:Zeeman} H_{\rm Z} = - {\bf \mu} \cdot {\bf B} = - g \mu_{\rm B} S^z B \, , \end{equation} where the \(z\) direction is here defined as the direction of the magnetic field.

In a similar way, magnetic ions interact with other magnetic ions through the dipole-dipole interaction. However, for most moments this is only a tiny effect that can be neglected. The major term deciding the interactions stem from the electrostatic forces. The combination of these forces and the Pauli principle will affect the energy levels of the system, resulting in the exchange interaction. There are a number of ways this interaction can appear, of which we mention only the two most important ones :

• \({\bf Direct exchange}\): Here, the electronic orbitals of the two ions overlap directly. If the spins of the electrons of the different ions have the same direction, the Pauli principle will make sure that they stay apart (the spatial part of the two-particle wavefunction must be odd as a function of interparticle distance - and is therefore zero where the particles meet). Hence, the electrostatic energy is lowered, and parallel alignment of spins is preferred.
• \({\bf Indirect exchange}\): Here, the electron orbitals on neighbouring magnetic ions do not overlap, but they are bridged by a non-magnetic ion (e.g. O\(^{2+}\)). If the electronic spins are different, they are able to ``visit one another by hopping over via the bridging ion. Despite the electrostatic repulsion, this hopping lowers the kinetic energy due to the Heisenberg uncertainty principle. If the spin quantum numbers are equal, the Pauli principle will completely prohibit such visits. In effect, an antiparallel spin alignment is (in most cases) energetically favourable.

The simple exchange interaction mechanisms described above are isotropic in spin space, since the underlying mechanisms do not depend upon the absolute orientation of the spins, only on their relative orientation. These interactions are described by the Heisenberg Hamiltonian: \begin{equation} H_{ij} = - J_{ij} {\bf S}_i \cdot {\bf S}_j , \end{equation} where \(i\) and \(j\) are labels of two different ions in the material. A positive value of the exchange constant \(J_{ij}\) favours a parallel alignment of the two spins, while a negative value favours an antiparallel alignment.

If anisotropies are present, the effective Hamiltonian changes. In the most extreme case, two of the spin dimensions are suppressed, and we reach the Ising Hamiltonian \begin{equation} H_{ij} = - J^z_{ij} S^z_i S^z_j . \end{equation} This Hamiltonian is much easier to deal with, as any state written in the \(S^z\) basis is immediately an eigenstate, and a classical description of the spins are sufficient.

The values of \(J_{ij}\) and \(J_{ij}^z\) can be several meV for \(i\) and \(j\) being nearest neighbours. In general, the interaction falls off rapidly as a function of distance, and it is often sufficient to include only first, and perhaps second, nearest neighbours.

Classical magnetic structures

In a magnetic solid, one must deal with the simultaneous interaction between all spins. This can give rise to many complex magnetic arrangements, or magnetic structures.

The physics can be described by the total Heisenberg Hamiltonian \begin{equation} \label{eq:Heisenberg} H = \sum_{\langle i,j \rangle} H_{ij} + \sum_j H_{\rm Z,j} = - \sum_{\langle i,j \rangle} J_{ij} {\bf S}_i \cdot {\bf S}_j - g \mu_{\rm B} B \sum_j S_j^z \, , \end{equation} where the summing convention here is so that the same pair, \(\langle i, j \rangle\), is only counted once. The solution of this Hamiltonian in the general case is a severely complex problem, which has puzzled physicists for most of a century.

It is observed by a number of experimental methods that many materials, which often can be described by (\ref{eq:Heisenberg}), become magnetically ordered below a certain phase transition temperature, or critical temperature, \(T_{\rm c}\). Some magnetic structures are stable even up to around \(T_{\rm c} \approx 1000\)~K.

A classical solution to (\ref{eq:Heisenberg}) is often a good approximation to the physical reality. At high temperatures, the system will always be in a disordered, or paramagnetic state. In this state, there is no correlation between different spins, i.e. \begin{equation} \left\langle {\bf s}_j \cdot {\bf s}_{j'} \right\rangle = 0. \end{equation}

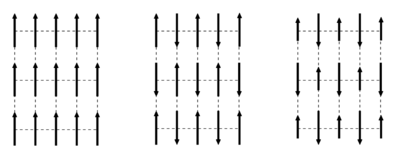
At low temperatures, the spins will typically find a state with long-range order. There are in general three main types of magnetically ordered structures, illustrated in Figure xx--CrossReference--magneticorder--xx. These three types are:

• Ferromagnetism: Here \(J_{ij} > 0\), and all spins are (on average) aligned in the same direction. Thus, the system has a resulting magnetisation.
• Antiferromagnetism: Here \(J_{ij}<0\), and the spins are divided into different sublattices (often two), each with the same magnetisation value. However, the total outer magnetisation of the antiferromagnet vanishes due to different orientations of the sublatticemagnetisations. By convention, the critical temperature for an antiferromagnet is denoted the N\`eel temperature, \(T_{\rm N}\), after Louis N\`eel who discovered antiferromagnetism.
• Ferrimagnetism: Here \(J_{ij} < 0\), and the spins are divided into sublattices aligned in different directions, like the antiferromagnet. However, the ferrimagnet still possesses a net magnetic moment, since the magnetisation value of the sublattices are different.This could be due to a different number of spins in the sublattices or to different spin values (as illustrated in Figure xx--CrossReference--magneticorder--xx).

Figure 1: The three main types of magnetically ordered structures. (left) The ferromagnetic structure, where all spins are aligned. (middle) A simple antiferromagnetic structure, with antiparallel alignment of spins and no net magnetic moment. (right) One type of a ferrimagnetic structure with antiparallel spin alignment, but still a net moment, here due to a difference in the spin values on two different sites.

Calculating the magnetic ordering vector

We will here make a brief introduction to magnetic structures for the simple case where all magnetic ions are crystallographically equivalent (only one magnetic ion per structural unit cell). This implies that the mean (or thermally averaged) magnitude of the ordered spin at a given site, \({\bf r}_j\), is independent of \(j\).

We denote the thermal average by \(\langle {\bf s}_{j} \rangle\).

We assume that we have a crystal of sufficiently large size that we can use periodic boundary conditions. Since all magnetic ions are equivalent, we have complete translational symmetry. Hence, the spin-spin interaction can only depend upon the relative position of the spins: \begin{equation} J_{ij} = J({\bf r}_i - {\bf r}_j) . \end{equation} The interaction part of the Hamiltonian can now be written in a slightly different form, where we first sum over all spins, and then over all the neighbours (denoted \(\delta\)) for each spin. To compensate for double-counting, we must in addition divide by a factor 2. In total, the Hamiltonial becomes \begin{equation} \label{eq:Heisenberg_neighbour} H = - \frac{1}{2} \sum_{j,\delta} J_\delta {\bf S}_j \cdot {\bf S}_{j+\delta} . \end{equation} For simplicity, we have assumed that the external field is zero. We now decompose the spin structure in its Fourier components \begin{equation} {\bf S}_{\bf q} = \frac{1}{\sqrt{N}} \sum_j {\bf S}_j \exp(i {\bf q} \cdot {\bf r}_j), \end{equation} where the inverse Fourier transform reads \begin{equation}\label{eq:Sj} {\bf S}_j = \frac{1}{\sqrt{N}} \sum_j {\bf S}_{\bf q} \exp(-i {\bf q} \cdot {\bf r}_j), \end{equation}

We further define the Fourier transform of the spin-spin interaction \begin{equation} \label{eq:Jq} J({\bf q}) = \sum_\delta J_\delta \exp(i {\bf q} \cdot {\bf r}_\delta) \, , \end{equation} which is a real quantity if the lattice has inversion symmetry (for each neighbour at \({\bf r}_\delta\), there is another neighbour at \(-{\bf r}_\delta\) with the same interaction constant). By using (\ref{eq:Sj}) and(\ref{eq:Jq}), we can transform (\ref{eq:Heisenberg_neighbour}) into the convenient expression :

\begin{equation} \label{eq:Heisenberg_q} H = - \frac{1}{2} \sum_{\bf q} J({\bf q}) {\bf S}_{\bf q} \cdot {\bf S}_{- \bf q} . \end{equation} Now, we use (\ref{eq:Sj}) and the identity \(S^2 = {\bf S}_j \cdot {\bf S}_j\) to reach \begin{equation} \label{eq:sumrule1} N S^2 = \sum_{{\bf q },{\bf q}'} {\bf S}_{\bf q} \cdot {\bf S}_{{\bf q}'} \exp(- i ({\bf q}+{\bf q}')\cdot{\bf r}_j ) . \end{equation} This must be satisfied simultaneously on all lattice sites, \(j\), which is a formidable amount of equations to solve. However, summing (\ref{eq:sumrule1}) over all sites gives a single (but relaxed) condition \begin{equation} \label{eq:sumrule2} N S^2 = \sum_{\bf q } {\bf S}_{\bf q} \cdot {\bf S}_{-{\bf q}} . \end{equation} Here, \({\bf S}_{\bf q} \cdot {\bf S}_{-{\bf q}}\) can be viewed as the square amount of the spin Fourier component of that particular {\bf q}. In this respect, (\ref{eq:sumrule2}) can be seen as a modified Pythagoras equation in \(N\) dimensions. Although a weaker requirement than the original (\ref{eq:sumrule1}), it is often sufficient to fulfill (\ref{eq:sumrule2}) to correctly determine the magnetic structure.

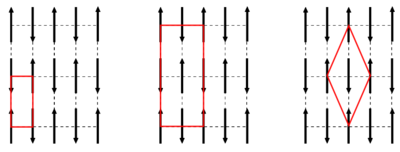
In this case, the ground state is found where only one Fourier component, \(S_{\bf Q}\), is non-zero. Here, the magnetic ordering vector, \({\bf Q}\), is the one that maximizes \(J({\bf q})\). The energy of the spin system is thus given by \begin{equation} E_{\rm min} = - NS^2 J({\bf Q}) . \end{equation} The detailed calculation behind this can be found in . Typical solutions to the minimization problem are

• \({\bf Q}={\bf 0}\): The ferromagnetic structure.
• \({\bf Q}\) lies on the Brillouin zone boundary. This means that \(\exp(i {\bf Q} \cdot {\bf r}_j) = \pm 1\) always. This gives two-sublattice, commensurate antiferromagnetic structures, as illustrated in Figure xx--CrossReference--magneticorder--xx. These structures are often found in nearest-neighbour dominated transition metal oxides.
• \({\bf Q}\) has another value. This often gives rise to incommensurate structures, e.g. helical (spiral) structures, often found in systems where interactions beyond nearest neighbours are substantial, e.g. in rare-earth metals. For a description of the magnetism of rare-earth elements and the underlying theory, we refer to the book by Jensen and Mackintosh .

Magnetic phase transitions

Magnetically ordered structures have in common that upon heating, the average ordered magnetic moment on each sublattice, or order parameter, decreases. When the order parameter reaches zero, at the transition temperature, \(T_{\rm c}\), the system becomes paramagnetic.

In first order phase transitions, the order parameter discontinuously drops to zero, and latent heat and thermal hysteresis is connected with the phase transition.

In second order phase transitions, the order parameter decreases continuously to zero, and the phase transition is reversible. Second order phase transitions can in general be described by the same universal theory, valid close to the transition temperature, where e.g. the order parameter varies as \begin{equation} {\langle {\bf S_Q} \rangle \propto \left(1-T/T_{\rm c} \right)^\beta}. \end{equation} The full description of these critical phenomena is outside the scope of these notes. A good introduction to neutron scattering studies of critical phenomena is found in the textbook by Collins.

In more complex systems, the magnetic phase diagram will contain more than one magnetic phase, e.g. the ordering vector, \({\bf Q}\), may vary (continuously or discontinuously) with temperature. We will, however, not discuss these more advanced cases here.

Perspectives

The detailed magnetic structure and its temperature dependence is of relevance for the classification of new magnetic materials, for example the multiferroic materials where the electric, magnetic and structural properties are strongly related. We also like to mention the use of magnetic phase transitions for magnetic cooling, and the many uses of magnetism in nanotechnology, e.g. for magnetic data recording.

Magnetic diffraction

We here present the magnetic scattering cross section for diffraction and show a few important examples.

The magnetic diffraction cross section

We will now consider the part of the magnetic scattering cross section in equation this equation from the Scattering_of_neutrons_from_magnetic_ions page, that is purely elastic in both the nuclear and the magnetic system. Hence, the energy \(\delta\)-function falls out and the completeness sum, \(\sum_f |\lambda_{\rm f}\rangle \langle \lambda_{\rm f}| = 1\), can be performed. We now obtain:

\begin{align} \label{eq:magnetic_diffraction0} \left.\frac{d\sigma}{d\Omega}\right|_{\rm magn. el.} &= \left(\gamma r_0 \right)^2 \left[ \frac{g}{2} F(q)\right]^2 \exp(-2W) \sum_{\alpha \beta} \left( \delta_{\alpha\beta}-\hat{q}_\alpha\hat{q}_\beta\right) \\ &\quad \times \sum_{\lambda_{\rm i}} p_{\lambda_{\rm i}} \sum_{j,j'} \exp(i {\bf q} \cdot ({\bf r}_{j'}-{\bf r}_{j})) \big\langle \lambda_{\rm i}| {\bf s}_{j}^\alpha {\bf s}_{j'}^\beta \big| \lambda_{\rm i}\big\rangle , \nonumber \end{align}

which for a static magnetic structure can be simplified to

\begin{align} \label{eq:magnetic_diffraction1a} \left.\frac{d\sigma}{d\Omega}\right|_{\rm magn. el.} = \left(\gamma r_0 \right)^2 \left[ \frac{g}{2} F(q)\right]^2 \exp(-2W) \biggr| \sum_{j} \exp(-i {\bf q} \cdot {\bf r}_{j}) \left\langle {\bf s}_{j,\perp} \right\rangle \biggr|^2 , \end{align}

where \(\langle \, \rangle\) here denotes thermal average and \({\bf s}_\perp\) is the spin component perpendicular to \({\bf q}\).

Equation \eqref{eq:magnetic_diffraction1a} plays the same pivotal role for magnetic diffraction as this equation from the The total cross section for a system of particles page, \(\dfrac{d\sigma}{d\Omega}\biggr|_{\rm coh} = \biggr|\displaystyle\sum_j b_j \exp(i \mathbf q \cdot {\mathbf r}_j)\biggr|^2 \), does for nuclear diffraction.

Paramagnetic scattering

A paramagnet is a collection of magnetic spins, where there is no correlation between different spins, i.e.

\begin{equation} \left\langle {\bf s}_j \cdot {\bf s}_{j'} \right\rangle = 0. \end{equation}

The scattering from a paramagnet is rather simple, since each spin scatters independently of the neighbouring spins. In fact, this is a magnetic version of incoherent scattering. In \eqref{eq:magnetic_diffraction0}, second line, only terms with identical position indices, of the type \({\bf s}_j \cdot {\bf s}_j\), contribute to the double sum. Hence, the dependence of \({\bf q}\) disappears. The five-fold sum can then be replaced with \(2 N s(s+1)/3\), where \(N\) is the number of spins, and the factor 2/3 comes from the fact that two out of three spin components are perpendicular to \(\bf q\). Hence, the result reads:

\begin{equation} \label{eq:paramagnetic_diffraction} \left.\frac{d\sigma}{d\Omega}\right|_{\rm paramagn. el.} = \frac{2}{3} N \left(\gamma r_0 \right)^2 \left[ \frac{g}{2} F(q)\right]^2 \exp(-2W) s (s+1). \end{equation}

Scattering from magnetically ordered structures

Figure 2: An illustration of the unit cell of the two-dimensional antiferromagnet. Left panel shows the nuclear unit cell, middle panels shows a unit cell, which is a factor two enlarged in both directions, and right panel shows the minimal antiferromagnetic unit cell.

We will here investigate the magnetic scattering from ordered magnetic structures, as described in the section Magnetism in materials. We assume the atoms to be located on an ordered lattice, as described on the Diffraction from crystals page. It should be noted that the magnetic unit cell used to describe ferri- and antiferromagnetically ordered structures is often larger than the structural unit cell. This is illustrated in Figure xx--CrossReference--fig:magnetic_unit_cell--xx.

We now develop the expression for magnetic diffraction in ordered structures, where we in analogy to nuclear diffraction utilize that the magnetic system can be described by repeated unit cells. Eq. (\ref{eq:magnetic_diffraction1a}) then becomes

\begin{align} \left.\frac{d\sigma}{d\Omega}\right|_{\rm magn. el.} = \left(\gamma r_0 \right)^2 \left[ \frac{g}{2} F(q)\right]^2 \exp(-2W) \biggr| \sum_{i,j} \exp(-i {\bf q} \cdot {\bf r}_{j}) \exp(-i {\bf q} \cdot {\bf \Delta}_{i}) \left\langle {\bf s}_{i,\perp} \right\rangle \biggr|^2 \, \end{align}

In analogy to the expressions for nuclear diffraction, the lattice sum over \(j\) produces delta functions, while the sum over the magnetic unit cell (\(i\)) gives what is known as the magnetic structure factor:

\begin{equation} \label{eq:magnetic_SF} F_{\rm M}({\bf q}) = \sum_{i} \exp(-i {\bf q} \cdot {\bf \Delta}_{i}) \left\langle {\bf s}_{i,\perp} \right\rangle . \end{equation} With this, the magnetic scattering cross section from an ordered structure ends up being

\begin{align} \label{eq:magnetic_diffraction2} \left.\frac{d\sigma}{d\Omega}\right|_{\rm magn. el.} &= \left(\gamma r_0 \right)^2 \left[ \frac{g}{2} F(q)\right]^2 \exp(-2W) \\ \nonumber &\quad\times \frac{N (2\pi)^3}{V_0} |F_{\rm M}({\bf q})|^2 \sum_{\boldsymbol\tau} \delta({\bf q}-\boldsymbol\tau-{\bf Q}) , \end{align}

where \({\bf Q}\) is the ordering vector of the magnetic structure, equations (\ref{eq:magnetic_diffraction2}) and (\ref{eq:magnetic_SF}) are equivalent to equation the equation for nuclear diffraction if we make the replacement

\begin{equation} b_j \longrightarrow \gamma r_0 \frac{g}{2} F(q) {\bf s}_{i,\perp} . \end{equation}

Figure 3: The first published neutron diffraction data was the determination of the antiferromagnetic structure in NiO, CoO, FeO, MnO, and \(\alpha\)-Fe\(_2\)O\(_3\). The data shown are scans on a two-axis diffractometer on a powder of MnO, (top) at 77 K (below \(T_{\rm N} = 120\) K) and (bottom) at 293 K. The low-temperature peak at \(2\theta = 12^\circ\) shows antiferromagnetic order with an ordering vector along (111). Note that there is still a broad bump at the (111) position at 293 K, typical for short-range magnetic order. From Ref. .

The magnitude of this magnetic scattering length is similar to the nuclear scattering lengths, since \(\gamma r_0 = 5.39\) fm and \(g F(q) s/2\) is of the order unity. Hence, the magnetic and nuclear scattering cross sections have similar magnitudes. For large values of S, e.g. in some transition metal salts, like Fe-oxides, or in most rare-earth compounds, the magnetic scattering can completely dominate the diffraction patterns.

In conclusion, magnetic diffraction is seen when the scattering vector equals a magnetic ordering vector (modulo a reciprocal lattice vector), and the intensity of the scattering is proportional to the square of the ordered moment and of similar magnitude as nuclear scattering. Hence, neutron scattering is a clearcut way to determine magnetic structures. Further, it is very useful for the determination of the ordered moments, especially for antiferromagnets where bulk techniques cannot determine the size of the moments.

Example

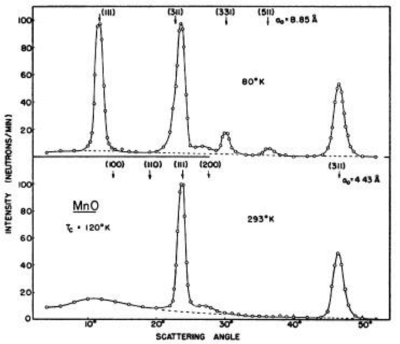
The existence of ordered antiferromagnets was predicted during the 1930'ies and 1940'ies, but the final proof was given by one of the first neutron diffraction experiments by C. Shull in Brookhaven, published already in 1951. For this, and for the invention of neutron diffraction in the first place, C. Shull was awarded the Nobel prize in 1994. Some original data, showing the proof of antiferromagnetism in MnO, are shown in Figure xx--CrossReference--fig:shull--xx.

←   Previous page: Magnetic neutron scattering
→   Exercises: Exercises in Elastic magnetic scattering
→   Next page: Inelastic magnetic scattering