Problem:The collimator
A horizontal collimator consists of a number of thin, parallel, equidistant sheets (like every \(n\)'th page in a book) of a neutron absorbing material, so that neutrons traveling in the "wrong" directions are eliminated. The distance between sheets is denoted \(D\) and the length of the sheets \(L\).
Question 1
Calculate the transmission, \(T\), as a function of horizontal neutron divergence, \(\eta_h\) (the horizontal deviation from the beam axis). You can assume that the sheets are infinitely thin. Further, assume that the position of individual collimator sheets are unknown (or equivalently that the collimator oscillates sidewards during the experiment).
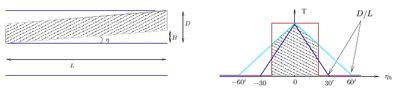
The transmission is only 100 % (\(T=1\)) when the beam is parallel to the collimator sheets. The part of the beam which is blocked by a collimator sheet (\(B\)) when the divergence is \(\eta\) scales roughly with the divergence when \(\eta\) is small
- \( \eta=\tan^{-1}\dfrac{B}{L} \approx \dfrac{B}{L} ,\)
where the parameters refer to Figure xx--CrossReference--fig:Collimator--xx, and the approximation is due to \(D \ll L\). The beam profile is therefore triangular as shown in the right part of Figure xx--CrossReference--fig:Collimator--xx.
Question 2
A collimator is described by the FWHM (full width at half maximum) of the transmission curve. Calculate the FWHM in terms of \(D\) and \(L\).
The maximum divergence before all the beam is absorbed by the sheets is
- \( \eta_{max}=\pm\tan^{-1}\dfrac{D}{L} \approx \pm\dfrac{D}{L} .\)
Since the shape of the transmission curve is triagular, the FWHM is the same as the maximum divergence
- \( \eta_{FWHM}=\tan^{-1}\dfrac{D}{L} \approx \dfrac{D}{L} .\)
Question 3
A typical collimator is 30' (or \(0.5^\circ\)) and has a length of \(L=200\) mm. What is the distance, \(D\), between the absorbing sheets?
This particular collimator has \(\eta_{FWHM}=30'=0.5^\circ\) and length \(L=200\) mm giving
- \( D = L \tan{0.5^\circ}=1.75 ~\text{mm} .\)
Question 4
A 60' collimator is inserted after the guide in the problem The neutron guide system. How does that affect the neutron flux for 4 Å and for 20 Å neutrons?
A collimator with \(\eta_{FWHM}=60'=1^\circ\) is inserted after the guide. At 4 Å all neutrons with divergence less than \(0.4^\circ\) are reflected in the guide and the rest are mostly absorbed. Hence there are no neutrons with divergence above \(0.4^\circ\) for the collimator to affect. The collimator still affects the neutrons with divergence less than \(0.4^\circ\), though. The combined (convoluted) beamprofile from the guide with \(0.4^\circ\) and the collimator with \(0.5^\circ\) are shown by the hatched area in the right part of Figure xx--CrossReference--fig:Collimator--xx (in the solution to question 1).
Neutrons with longer wavelengths ('colder') however have a larger critical angle in the guide, for example 20 Å neutrons have a critical angle of \(2^\circ\), i.e. all neutrons from the guide have smaller divergences than \(2^\circ\). A collimator with \(60'=1^\circ\) is fully contained within the beam profile from the guide, hence the resulting beam profile is the triangle of the 60' collimator (green line on figure Figure xx--CrossReference--fig:Collimator--xx).