Problem:The moderator temperature

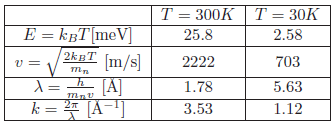
In typical sources for neutron scattering purposes, the neutrons are moderated by water. These "thermal" neutrons will (almost) reach thermal equilibrium with the moderator. Calculate the equivalent energy, \(E\), and velocity, \(v\), of a thermal neutron, moderated by water at \(T_{{\rm H}_2 {\rm O}} = 300\,\text{K}\).

Question 1

Calculate the corresponding de Broglie wavelength, \(\lambda\), and wavenumber, \(k\).

Expand

Hint

The energy at a specific temperature is \( E = k_B T \) [meV] and the neutron velocity at a specific temperature is

\begin{equation*} v = \sqrt{\frac{2k_BT}{m_n}} \end{equation*}

with unit [m/s].

Use the constants \( m_n = 1.675 \times 10^{-27} \text{kg}\), \(1 \text{eV} = 1.602 \times 10^{-19} \text{J}\), \( k_B = 1.38 \times 10^{-23} \text{J/K} = 8.61 \times 10^{-5} \text{eV/K}\).

Expand

Hint

The de Broglie wavelength can be calculated from \(\lambda = h / (m_n v) \) [Å].

Expand

Solution

The calculated values can be found in the table of the solution of the next question.

Question 2

Perform the same calculations for neutrons thermalised by liquid H\(_2\) at \(T_H = 30 \text{K}\).

Expand

Solution

Table 1: Specifics for neutrons moderated at 30 K and 300 K.

The values shown are shown in Table xx--CrossReference--tab:specs_moderated_neutrons--xx.

Question 3

For each of the two types of moderators above, calculate the ratio of intensities: \(I\)(4 Å)/\(I\)(20 Å).

Expand

Solution

\begin{equation*} \frac{I(\lambda_1)}{I(\lambda_2)} = \left(\frac{\lambda_2}{\lambda_1}\right)^5 \exp\big( {-C(T)(\lambda_1^{-2} -\lambda_2^{-2} )} \big) \end{equation*} where \( C(T) = h^2 / (2 m_n k_B T) \), hence \(C(30\text{K}) = 3.17\times 10^{-19} \text{m}^2\) and \(C(300\text{K}) = 3.17\times 10^{-20}\text{m}^2\).

So for \(T=30 \text{K}\)

\begin{equation*} \frac{I(4\tt{Å})}{I(20\tt{Å})} = 5^5 \cdot \exp\big( -3.17\times 10^{-19}\cdot 6\times 10^{18} \big) = 466 \end{equation*}

since \((4 \times 10^{-10} \text{m})^{-2} - (20 \times 10^{-10} \text{m})^{-2} = 6 \times 10^{18} \text{m}^{-2}\).

For \(T=300 \text{K}\)

\begin{equation*} \frac{I(4\tt{Å})}{I(20\tt{Å})} = 5^5 \cdot \exp\big( {-3.17\times 10^{-20}\cdot 6\times 10^{18}} \big) = 2584 \end{equation*}

Question 4

Many neutron instruments utilize a band of incident wavelength, \(\Delta \lambda\). For many instruments, \(\Delta \lambda / \lambda\) is almost constant and is of the order 0.1%-10%, depending on instrument type. For instruments with these bandwidths, calculate the ratio of the neutron fluxes at the sample: \(\Psi\)(4 Å)/\(\Psi\)(20 Å).

Expand

Solution

Figure 1: A sketch of a moderator spectrum and the intensity in a particular bandwidth at 4 Å and 20 Å respectively

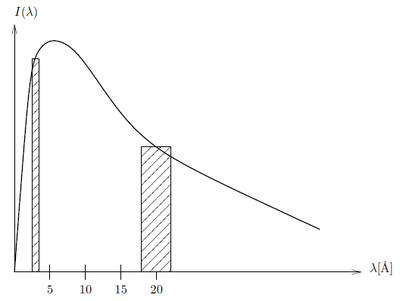
According to the calculation above apparantly there is several orders of magnitude more intensity of the neutrons at 4 Å than at 20 Å. If we however take a look at a small window of energies around 4 Å and 20 Å, respectively and integrate over these the ratios are not so extreme: Consider the intensity constant within the small wavelength bands \(\lambda_1-\Delta \lambda_1; \lambda_1+\Delta \lambda_1\) and \(\lambda_2-\Delta \lambda_2; \lambda_2+\Delta \lambda_2\). The relative intensity between wavelength bands is

\begin{equation*} \frac{I(\lambda_1\pm\Delta\lambda_1)}{I(\lambda_2\pm\Delta\lambda_2)} = \frac{\displaystyle\int_{\lambda_1-\Delta \lambda_1}^{\lambda_1+\Delta \lambda_1} I(\lambda_1)d\lambda_1} {\displaystyle\int_{\lambda_2-\Delta \lambda_2}^{\lambda_2+\Delta \lambda_2} I(\lambda_2)d\lambda_2} \approx \frac{I_1\cdot 2\Delta \lambda_1}{I_2\cdot 2\Delta \lambda_2} \end{equation*}

The approximation is shown in Figure xx--CrossReference--fig:moderator_spectrum--xx. If \({\Delta \lambda}/{\lambda}=10\%\) and \(\lambda_1=4\) Å and \(\lambda_2=20\) Å then \(\Delta\lambda_1=0.4\) Å and \(\Delta\lambda_2=2\) Å so at 30 K where \(I_1 / I_2 = I(4Å) / I(20Å) = 466\)

\begin{equation*} \frac{I(4\pm0.4)}{I(20\pm2)} = 466\frac{0.8}{4} = 93.2 \end{equation*}

and at 300 K where \({I_1} / {I_2}={I(4Å)} / {I(20Å)} = 2584\)

\begin{equation*} \frac{I(4\pm0.4)}{I(20\pm2)} = 2584\frac{0.8}{4} = 517 \end{equation*}