Problem: Estimating the circle area

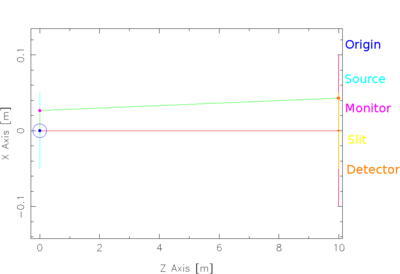
Construct a simulation with a square neutron source, which emits neutrons in a preferred direction. Focus the source output to a position-sensitive detector, which is much further away than the source size. Verify that the detector is completely illuminated, but that still all emitted neutrons rays are detected. Then place a circular slit very close to the detector.

Use your results to estimate the value of \(\pi\). Perform the simulations for a varying number of neutron rays, \(N\), in the interval \(10^4 - 10^8\). Make a few simulations for each value of \(N\). Determine how the simulation uncertainty depends on \(N\).

Hint

See the Monte Carlo simulation of neutron instrumentation page.

Solution

The simulation setup is shown in the left panel of Figure xx--CrossReference--fig:circle_instr--xx. It is seen in the simulation result on the right panel of Figure xx--CrossReference--fig:circle_instr--xx that the intensity in the monitor (before the circular slit) and detector (after the circular slit) is the same irrespective of the number of traced rays \(N\). However, the uncertainty in the simulated intensity decreases with increasing \(N\). The simulated number of rays hitting inside the circle is \(N_i\). For large \(N\) the simulation uncertainty of the number of rays hitting inside the circle \(\Delta N_i\) is approximately \(\sqrt{N_i}\). Hence for \(N = 10^8\), \(\Delta N_i = 10^4\), and the number of rays hitting inside the circle is \(N_i=0.7854 \pm 0.0001\cdot 10^8\).

Figure 1: A visualisation of the used McStas instrument. One neutron ray (green) is traced in the image. Notice the aspect ratio of the axes.

The ratio between the area of a unit circle and a square with the same width is \(A_c/A_s=\pi/4\), the value of \(\pi\) is hence estimated by the Monte Carlo simulation to be

\(\pi=\dfrac{A_c}{A_s} \cdot 4 \quad\to\quad \dfrac{N_i}{N}\cdot 4=\dfrac{0.7854 \cdot 10^{8}}{1.0000\cdot 10^{8}} \cdot 4=3.1416\pm 0.0001 .\)

• 

  McStas simulation using \(N=10^4\) rays showing that all rays hit a detector of area \(10\times10\) cm\(^2\) (left). Inserting a circular slit of diameter 10 cm reduces the number of neutrons to \(N=7839\) (right).
• 

  McStas simulation using \(N=10^6\) rays showing that all rays hit a detector of area \(10\times10\) cm\(^2\) (left). Inserting a circular slit of diameter 10 cm reduces the number of neutrons to \(N=0.7839\times10^6\) (right).
• 

  McStas simulation using \(N=10^8\) rays showing that all rays hit a detector of area \(10\times10\) cm\(^2\) (left). After the circular slit only \(N=0.785302\times10^8\) rays are left (right).