Reflectivity of periodically stratified media

Figure 1: The reflectivity from a periodic iron/silicon multilayer. The insert shows a schematic of the scattering length density as a function of depth in the sample. The bilayer repeat distance is given be \(\Lambda\).

Periodically stratified media represent an important category of thin multilayer materials as certain physical aspects, for example optical or electronic properties, can be enhanced or suppressed depending on their structure. This behaviour can be exploited in technology, or in reflectivity experiments when the contribution from certain structural components in the sample can be increased.

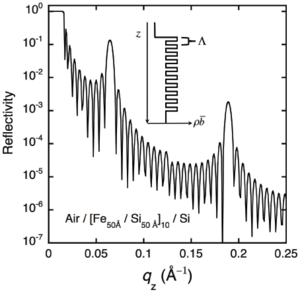
An example of the scattering length density of a periodically stratified sample is shown in Figure xx--CrossReference--reflectivityfig:SL--xx. The sample is formed of ten bilayers, each bilayer consisting of 50 Å Fe and 50 Å Si. The total thickness of the bilayer is therefore \(\Lambda = 100\) Å.

The figure also shows the calculated reflectivity from the sample. Kiessig fringes are clearly visible with a spacing that corresponds roughly to the total thickness of the film. The reflectivity also shows peaks at multiples of \(q_z \approx 2\pi/\Lambda\). These peaks are analogous to Bragg peaks, given by the periodicity of the layers in the sample. They are quite broad in \(q_z\) in the example, but become sharper as more bilayers are added. These peaks are usually quite far from \(q_c\) and can often be analysed using the first Born approximation. It must be noted that reflectivity is not sensitive to the atomic structure of the layers, and that these peaks will appear whether the layers are amorphous or monocrystalline. However, analysis of these peaks can give sensitive information about the structure of an individual period in the sample, in much the same way as the analysis of Bragg peaks from single crystals can be used to determine atomic positions in a diffraction experiment.

In the example, the thicknesses of the two components of the bilayer are equivalent. This results in the even harmonics of the Bragg peaks to be suppressed, i.e. the Bragg peaks appear at \(q_z \approx 2\pi M/\Lambda\), where \(M = 1, 3, 5, ...\). If the thicknesses are not equivalent, the even harmonics will begin to appear. Reflectivity measurements at these positions are therefore very sensitive to the structural quality of the sample.

It may be noted that the reflectivity of the first harmonic is quite large. This has been exploited in modern neutron optics. If many bilayers are deposited such that \(\Lambda\) is slowly varied as a function of depth, the reflectivity will show many such intense Bragg peaks with slightly different \(q_z\). The peaks will add together and give a high reflectivity that decreases slowly with increasing \(q_z\). The net effect is almost as good as having a film with a very large \(q_c\), even beyond \(q_z = 0.1\) {Å}\(^{-1}\). These films are the supermirrors we discussed on the page on neutron guides.