Problem: A neutron guide system

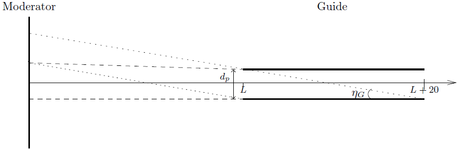
The neutron flux from a moderator can be described by the temperature of a Maxwellian distribution. Assume we have a square cold source \(15 \times 15\) cm\(^2\) with \(T=30\) K with a neutron flux of \(10^{12}\) neutrons/s/cm\(^2\)/steradian, corresponding to values for ESS or ILL. Use this moderator to construct a 20 m neutron guide system with \(m=1\) starting 1.5 m from the moderator, similar to the one in problem the neutron guide system.

Question 1

Simulate this system and try to reproduce the analytical results of the problem the neutron guide system. Use the McStas guide values \(\alpha=0\), \(W=0\), \(R_0=1\), and \(m=1\) (to remove the effect of the guide, use \(m=0\)).

Solution

Figure 1: Simulated divergence and intensity for a monochromatic beam of 4 Å after a guide with \(m=0\) (pinhole collimator).

Using a wavelength interval of 4 Å to 20 Å neutrons focused in the guideentrace and monitoring the intensity at the guideexit, there is no difference between the transmitted intensity through the guide if it is placed at \(L=1.5\) m (slightly underilluminated for 20 Å neutrons) or \(L=1.4\) m (not underilluminated for \(\lambda< 20\) Å).

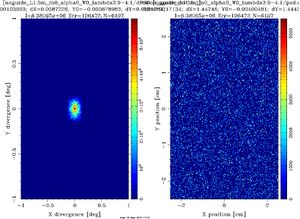
On divergence monitors placed at the guide entrance and -exit it is seen that in the case \(m = 1\) a square uniform distribution of neutrons are exiting the guide with maximum divergence \(0.4^\circ\) for \(\lambda=4\pm0.1\) Å neutrons and \(2^\circ\) for \(\lambda=20\pm0.1\) Å, as calculated in the problem the neutron guide system. In the case \(m = 0\) the neutron distribution is pyramidal (like a collimator - see problem the collimator) with maximum divergence \(0.14^\circ\). See also Figure xx--CrossReference--fig:beamprofile--xx.

By simulation (see Figure xx--CrossReference--fig:noguide--xx and (xx--CrossReference--fig:guide_m1--xx)) of the intensity at the end of the \(0.05 \times 0.05 \times 20\) m\(^3\) guide (placed 1.5 m after the moderator with \(\lambda = 4\) Å and \(\Delta \lambda = 0.1\) Å), the relative intensity

\(\dfrac{\mathcal{I}^{PSD}_{m=1}}{\mathcal{I}^{PSD}_{m=0}} \approx 30. \)

Figure 2: Simulated divergence and intensity for a monochromatic beam of 4 Å after a guide with \(m=1\).

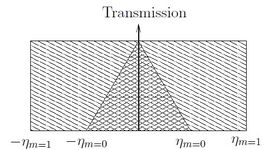
In the calculated example the neutron guide system the beamprofile at the end of the guide was not considered, hence giving approximately a factor 4 smaller relative intensity as shown in Figure xx--CrossReference--fig:transmission--xx.

Figure 3: Beamprofile through a guide with $m=0$. At divergence $\eta _{G}$ (dotted lines) only neutrons from the outermost part of the entering beam will pass through the guide, whereas for divergence 0 (dashed lines) all neutrons that pass into the guide will be transmitted.

In one dimension the integrated intensity is given by

Figure 4: Transmission as function of divergence in case of reflecting guide (\(m=1\)) or non-reflecting guide (\(m=0\)).

\(\mathcal{I}_{m=0}=\displaystyle\int_{-\eta_0}^{\eta_0}I\cdot(1-\dfrac{\eta}{\eta_0})\text{d}\eta=I\cdot\eta_0\)

in the \(m=0\) case. In the \(m=1\) case

\(\mathcal{I}_{m=1}\displaystyle\int_{-\eta_1}^{\eta_1}I\text{d}\eta=2I\cdot \eta_1 .\)

In two dimensions the relative integrated intensity is given by the relative transmission integrated over the divergence angles

\(\dfrac{\mathcal{I}_{m=1}}{\mathcal{I}_{m=0}} = \dfrac{\left(2\eta_{m=1}\right)^2}{\eta_{m=0}^2} = 4\left(\dfrac{\eta_{m=1}}{\eta_{m=0}}\right)^2 .\)

Since \(\eta_{m=0}= 0.14^\circ\) and \(\eta_{m=1}= \theta_c= 0.4^\circ\) at \(\lambda=4\) Å the relative intensity should be

\(\dfrac{\mathcal{I}_{m=1}}{\mathcal{I}_{m=0}}=4\dfrac{0.4^2}{0.14^2}=33 .\)

Question 2

Exchange the \(m=1\) guide with a multilayer guide of \(m=2\) with the parameters (McStas defaults): \(\alpha = 4.38\) and \(W=0.003\). Repeat the simulations to investigate the effect of the new guide material. One suggestion could be to investigate how intensity and divergence behave as a function of neutron wavelength for the two different guides.

Solution

Figure 5: Simulated divergence and intensity for a monochromatic beam of 4 Å after a guide with \(m=2\), \(\alpha=4.38\) and \(W=0.003\).

The reflectivity from a supermirror depends on the scattering vector (see e.g. the McStas component manual), the dependance above the critical scattering vector is controlled by McStas parameters \(\alpha\) and \(W\).

If \(m=2\), but \(\alpha=0\) and \(W=0\) equivalent of total reflectivity up to \(Q=2Q_c\), the relative intensity with/without guide is increased by a factor \(2^2=4\) to

\(\dfrac{\mathcal{I}_{m=2}}{\mathcal{I}_{m=0}} = 4 \dfrac{\mathcal{I}_{m=1}}{\mathcal{I}_{m=0}}\sim 130 .\)

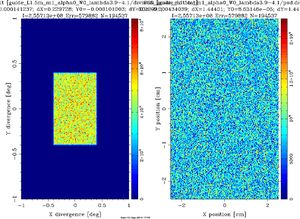
Now \(m=2\), \(\alpha=4.38\) and \(W=0.003\) to simulate a real supermirror, giving a small slope \(\alpha\) in the reflectivity above \(Q=Q_c\) until a soft \(W=0.003\) cutoff at \(Q=2Q_c\). The maximum divergence at the guideexit is now \(0.8^\circ\) and the beamprofile is no longer uniform, but has higher intensity at smaller angles as seen in Figure xx--CrossReference--fig:guide_L1.5m_m2--xx. However, intensity is gained with respect to the \(m=1\) case

\(\dfrac{\mathcal{I}^\text{realistic}_{m=2}}{\mathcal{I}_{m=1}} = 3.\)