Problem:Polydisperse spheres: Difference between revisions
m (1 revision imported) |
m (Wikiadmin moved page Problem: Polydisperse spheres to Problem:Polydisperse spheres) |
(No difference)
| |
Latest revision as of 15:28, 20 September 2020
We imagine a solution of polydisperse spheres with volume fraction \(\phi\). When we can assume $S(q)=1$ (typically for low concentrations, \(\phi \ll 1\)), the total SANS cross section per sample volume is given by
- \( I(q)= \phi V (\Delta \rho)^2 P(q), \,\)
where \(V\) is the volume of the particle.
Question 1
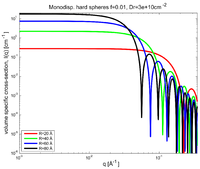
Assume that the volume fraction is \(\phi= 0.01\) and that the excess scattering length density is \(\Delta\rho=3\cdot 10^{10} \rm{cm} / \rm{c}m^3\). Using the form factors found in the problem Scattering form factor for spheres, calculate and plot the volume specific cross section from spherical particles of radii \(R=20\) Å, \(R=40\) Å, \(R=60\) Å and \(R=80\) Å respectively if they are considered monodisperse and dilute.
The total SANS scattering cross section per sample volume for dilute monodisperse hard spheres of selected sizes at fixed volumefraction is shown in Figure xx--CrossReference--fig:XS_monodisp_hard_spheres_phi0p01_deltarho3e10--xx.
It is seen that it is similar to the form factors shown in Question 3 of Scattering form factor for spheres, the only difference is the scaling due to the prefactors of the formfactor.
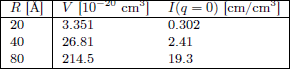
The interpolated values for \(I(q=0)\) with a fixed volumefraction of \(\phi=0.01\) are shown in Table xx--CrossReference--tab:dilute_monodisperse_spheres--xx.
Question 2
Now, assume instead that your sample of spheres is weakly polydisperse, and that it basically follows a Gaussian distribution, with \(R_{\rm av}=R\) and with a relative standard deviation of 20 % giving the volume specific scattering cross-section
- \( I(q) = \phi V (\Delta\rho)^2 \displaystyle\int {\rm d}R \ D(R)\cdot P(q,R) ,\)
where \(V=4\pi R_{av}^3 /3\) is the average volume of the particles with average radius \(R_{av}\) but distributed by the size distribution \(D(R)\). The formfactor amplitude is denoted \(P(q,R)\). An appropriate integration range might be \(R\in[R_{av}-3\sigma;R_{av}+3\sigma]\).
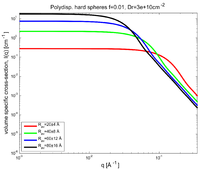
Plot the volume specific scattering cross-section in the polydisperse case for (at least) the \(R=60\) Å sample.
We consider now a polydispersity of the spheres of 20% in a Gaussian distribution, i.e.
- \( D(R)=\dfrac{1}{\sqrt{2\pi}\sigma} e^{-\tfrac{(R-R_{av})}{2\sigma^2}} \)
with \(\sigma=0.2R\).
The cross-section per sample volume for dilute polydisperse hard spheres is shown in Figure xx--CrossReference--fig:dilute_polydisperse_spheres--xx. The 20% smearing has now completely removed the ripples on the curve in the high-\(q\) tail and replaced it by a power law. The integration over sizes has been performed numerically in the range \([R_{av}-3\sigma;R_{av}+3\sigma]\).
Question 3
For higher particle concentrations, the particle-particle interactions generally have to be taken into account in the modeling of the scattering intensity via the structure factor, \(S(q)=|S(\mathbf{q})|^2\). The particles interact with a hard-sphere volume fraction \(\phi\).
This structure factor may be combined with the form factor to yield the total volume specific scattering cross section.
Use the locally monodisperse approximation (this equation). An appropriate integration range for the Gaussian distribution might be \(R\in[R_{av}-3\sigma;R_{av}+3\sigma]\).
The expression for \(S(q)\) has been calculated (using the Percus-Yevick approximation for the closure relation[1])
- \( S(q,R) = \dfrac{1}{1+\dfrac{24\phi}{2Rq}\cdot G(2Rq) } ,\)
where in this equation
- \( \begin{align*} G(A) &=\dfrac{\alpha(\sin{A}-A\cos{A})}{A^2}+\dfrac{\beta(2A\sin{A}+(2-A^2)\cos{A}-2)}{A^3}\\ &\quad +\dfrac{\gamma(-A^4\cos{A}+4((3A^2-6)\cos{A}+(A^3-6A)\sin{A}+6))}{A^5} \end{align*} \)
and
- \( \alpha=\dfrac{(1+2\phi)^2}{(1-\phi)^4}, \quad \beta=\dfrac{-6\phi(1+\phi/2)^2}{(1-\phi)^4}, \quad \gamma=\dfrac{\phi \alpha}{2}. \)
Calculate and plot the scattering cross-section per sample volume for the \(R=60\) Å polydisperse spheres for volume fractions of 1 %, 5 %, 10 %, 25 % and 50 % using the expression above for the structure factor.
The cross-section per sample volume for interacting hard spheres is shown in Figure xx--CrossReference--fig:interacting_polydisperse_spheres--xx . From the figure it is seen that increasing volumefraction of the spheres, and thereby increasing interaction between the spheres, gives an increasingly well-defined peak at \(q\approx \pi / R=0.05\) Å\(^{-1}\). Notice also how the low-\(q\) intensity decreases with increasing volumefraction (interaction via the structurefactor).
- ↑ J.S. Pedersen, Neutrons, X-rays, and Light (Elsevier, 2002)