Problem:The beam port
We define the intensity from a point source emitted in the solid angle \(d\Omega\) by \(I=\int d\Omega \Psi\).
Question 1
Consider first a point source which emits flux \(\Psi_0\) [cts/(s\(\cdot\)ster)]. Calculate the intensity at position \(L\) downstream from the source through a small area \(\Delta A\) (e.g. of a detector).
The intensity will be given by
- \( I=\displaystyle\int d\Omega \, \Psi_0 = \displaystyle\int_{\Delta A} dA \, \dfrac{\Psi_0}{L^2} \approx \dfrac{\Psi_0}{L^2} \Delta A \)
Question 2
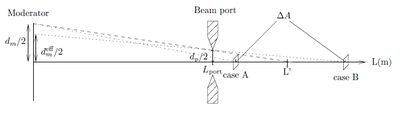
Consider now a moderator of a typical useful size of \(150\times 150\) mm\(^2\). The moderator emits neutrons isotropically and uniformly over its surface with "source flux" \(\Psi_0\) [cts/(s\(\cdot\)m\(^2 \cdot\)ster)]. A beam port (slit) of size \(50\times50\) mm\(^2\) is placed 4 m from the moderator face. Consider a small area \(d A\) centered at the moderator-beam port axis; downstream from the beam port. Calculate how the neutron flux through \(d A\) varies with distance, \(L\), from the moderator.
The variation in distance between any point of the moderator and any point of the beam port can safely be ignored. Gravity can be neglected.
At a certain position (\(L'\)) of \(d A\), the beamport it starts to block part of the view to the moderator.
In the following the width and height of the square moderator is denoted \(d_m\) and the width and height of the square beamport denoted \(d_p\). For \(L<L'\) (case A, underilluminated beam port), the moderator is not shielded by the beamport, but for \(L>L'\) (case B) the moderator is shielded by the beamport, see Figure xx--CrossReference--fig:Beamport--xx. In general, the integrated intensity radiated in \(d\Omega\) from a source with area \(A_m\) is
- \( \mathcal{I} = \displaystyle\int dA_m \, I = \displaystyle\int dA_m \displaystyle\int d\Omega \, \Psi_0 = \displaystyle\int dA_m \displaystyle\int dA \, \dfrac{\Psi_0}{L^2} \approx A_m\, \Delta A\, \dfrac{\Psi_0}{L^2} ,\)
where variations in the distance from different places on the source to the point \(L\) has been neglected. The flux is then
- \( \Psi = \dfrac{\mathcal{I}}{\Delta A} = A_m\, \dfrac{\Psi_0}{L^2} .\)
Inserting a beamport does not change the flux for \(L<L'\) ,
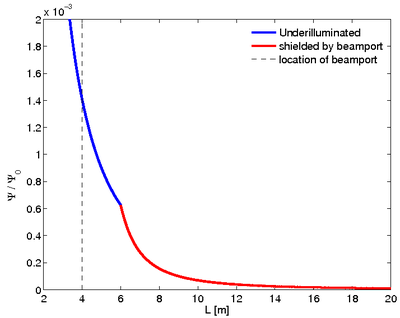
- \( \Psi_{L<L'} = A_m \dfrac{\Psi_0}{L^2} = d_m^2 \dfrac{\Psi_0}{L^2} = 0.0225 \dfrac{\Psi_0}{L^2}, \)
where \(L\) is the distance from the source (moderator) with area.
The flux at \(L\geq L'\) is
- \( \begin{align*} \Psi_{L>L'} &= A_m^{\text{eff}} \dfrac{\Psi_0}{L^2} \\ &= (d_m^{\text{eff}})^2 \dfrac{\Psi_0}{L^2} \\ &= d_p^2 \left(\dfrac{L}{L-L_{\text{port}}}\right)^2 \dfrac{\Psi_0}{L^2} \\ &= d_p^2 \dfrac{\Psi_0}{(L-L_{\text{port}})^2} \\ &= 0.0025 \dfrac{\Psi_0}{(L-4)^2}, \end{align*}\)
since the beamport 'shields' the moderator giving an effective source size of \((d^{\text{eff}})^2\). I.e. effectively the detector (\(\Delta A\)) sees a virtual source of size \((d_m^{\text{eff}})^2\) at distance \(L-L_{\text{port}}\). The flux is plotted in Figure xx--CrossReference--fig:Flux_beamport--xx.
Question 3
The divergence, \(\eta\), of a neutron is defined as the angular deviation of the neutron velocity to the main axis. Calculate the maximal divergence as a function of \(L\) for the cases described above.
The maximum divergence in the the underilluminated case where \(L<L'\) is
- \( \eta_{L<L'} = \tan^{-1}\dfrac{d_m}{2L} .\)
Similarly, the maximum divergence in the case where \(L\geq L'\) is
- \( \eta_{L\geq L'} = \tan^{-1}\dfrac{d_p}{2(L-L_{\text{port}})} .\)