Monte Carlo simulation of neutron instrumentation
Even in the simplest cases, it is not straightforward to calculate the optics of a neutron guide system. This is illustrated, e.g., by considering multiple bounces in a neutron guide system, see problem The neutron guide system. An accurate calculation of the properties of a complete and realistic neutron instrument becomes almost hopeless, and various other schemes must be applied.
One approach is the approximate, analytical calculations, made for determining the instrument resolution, which was performed around 1970 by Cooper and Nathans[1] and Popovici[2]. Calculations of this type have been extremely useful for many types of neutron instruments over the past decades, in particular triple-axis spectrometers, which are mostly used for elastic and inelastic measurements on single crystals, with high \(q\)-resolution. The triple-axis spectrometer was presented on the pages on Instrumentation in section Instruments for inelastic neutron scattering.
An alternative way to describe neutron instruments is to perform computer simulations of neutron motion. This can give essentially correct descriptions of neutron instrument models. The results are, however, subject to statistical sampling errors, always present in computer simulations (as in real experiments).
This page gives an introduction to Monte Carlo simulations and to existing Monte Carlo ray-tracing packages for neutron scattering.
Introduction to the Monte Carlo technique
Monte Carlo simulations are in general a way to perform approximate solutions to complex problems by use of random sampling. The phrase "Monte Carlo" comes from the generous use of random numbers, which resembles the gambling of the famous Monaco casino, and the method was originally designed to facilitate calculations of neutron physics - more precisely for the Manhattan project. For the history of the Monte Carlo technique, we refer to an excellent essay by one of its inventors[1].
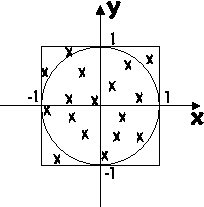
A simple example of Monte Carlo simulations
As an introduction, we consider a simple example. We intend to estimate the area of an object. For simplicity let us consider the unit circle, \(x^2 + y^2 \leq 1\), as shown in Figure xx--CrossReference--fig:MCcircle--xx. We now select \(N\) points randomly in the square of known area, \(A_{\rm s}=4\), that contains the circle fully. The area is defined by
\begin{equation}\label{dummy644155134} -1 \leq x \leq 1 \; \wedge \; -1 \leq y \leq 1 . \end{equation}
Each of the selected points inside this square are determined by retrieving independent, random values of \(x\) and \(y\) from a (pseudo-) random number generator. We will not here dwell on the issue of random number generation, which is described elsewhere[2], we only mention that such generators exist with specifications usefor for our purpose.
We now calculate the number of points, \(N_i\), that fall inside the unit circle. For large \(N\), the fraction of accepted points will according to the law of large numbers approach the ratio of the areas:
\begin{equation}\label{dummy702629630} \dfrac{N_i}{N} \rightarrow \dfrac{A_{\rm c}}{A_{\rm s}}. \end{equation}
Hence, this "numerical experiment" can be used to estimate the value of the circle area, \(A_{\rm c}\). Of course, the answer of this example is well known: The ratio is \(\pi/4\).
On Monte Carlo methods
Monte Carlo techniques can be used to solve problems much more complex than the example above. This may involve complex figures and/or a number of branches (choices between different possibilities). Here, analytical solutions are often impossible, making the Monte Carlo method show its full virtue.
In general, Monte Carlo techniques can be used for problems in different fields:
- In physics, the method can describe a number of many-body problems. E.g. in high-energy physics where a particle under consideration can be either absorbed, scattered, or converted into other particles.
- In mathematics, the method can be used to solve complex integrals in many dimensions with complex boundary conditions.
- In finance theory, the method is used to estimate the effect of uncertainties in market values.
- In computer science, the method has been used to optimize multi-variable functions.
Methods for variance reduction
As with all stochastical methods (including experiments), Monte Carlo methods are prone to statistical errors or variances. To reduce the statistical errors of simulations, a number of variance reduction methods have been designed. We here mention
- Stratified sampling. To ensure that the sampling is spread evenly, one would divide the parameter space up into mutually exclusive strata, and sample a given amount of each strata. In the circle example above, one could divide the area up into smaller quadrates and sample equally often from each.
- Importance sampling. When it can be shown that some places in parameter space is more crucial to the final result than others, one can chose to sample more often in the important regions. If the problem was e.g. to calculate the average height over sea level of a landscape, one would measure the mountain more careful than the lake, i.e. the Monte Carlo sampling would be denser at the mountain. In the stratified version of the circle example, one would sample more often in areas that contain a part of the circle rim, while completely filled or empty areas need little sampling.
Monte Carlo Ray-tracing
We will not explain the general Monte Carlo technique in further detail, but refer to a number of textbooks[3].
Rather, we specialize immediately to the method relevant for our purpose. This is known as Monte Carlo ray-tracing and can be performed to study objects which travel along a path (a ray), and can be (partially) absorbed or scattered into another direction, but not converted into other types of radiation. The most known example of this is light, and this type of ray-tracing is frequently used to generate realistic illumination in 3D computer graphics.
In a scientific environment, ray-tracing can be used to study non-interacting radiation, e.g. neutrons or X-rays. We will now dive into the explanation of ray-tracing simulations for this purpose.
- ↑ N. Metropolis. http://library.lanl.gov/la-pubs/00326866.pdf
- ↑ See the home page of the Mersenne Twister Algorithm http://www.math.sci.hiroshima-u.ac.jp/~m-mat/MT/emt.html
- ↑ D.P. Landau and K. Binder. A Guide to Monte Carlo Simulations in Statistical Physics. (Cambridge, 2005).
Monte Carlo ray-tracing packages for neutrons
In the early 1990'ies, simulation of the optics in a neutron instrument was performed mostly by monolithic Monte Carlo codes. Although being marvelous pieces of work, these codes were mostly written as one-person projects with limited manpower resources. Hence, the codes were designed to solve only one particular problem. They were thus subject to lack of generality, possible programming mistakes, low documentation level, and limited user-friendliness. (One notable exception from this is the package NISP.)
Today, a fair number of well-tested and documented general freeware packages exists for neutron ray-tracing simulations. Each package has the aim of enabling neutron scientists (and students) to quickly set up simulations. The development projects of the package co-exist in an atmosphere of collaboration and friendly competition for users. The collaboration between the three European packages were 2004-2012 supported by a European Union research project, MCNSI[6]. The 5 currently maintained packages are listed in Table xx--CrossReference--tab:MCpackages--xx.
The main author of these notes is also a co-author of the McStas package. However, we have kept the text part of these notes free from reference to any particular package, to the extent possible. The hands-on problems om simulations found on the McStas simulation projects page are related directly to the McStas package, but could with little effort be "translated" into covering any other simulation package.
Describing the neutron optical components
In the simulation packages, the individual optical components (or modules), like source, guide, sample, and detector, are parametrized and pre-programmed. Each package contains a library of well-tested components that cover the most often used optical ones, as well as some model samples. It is, however, possible for the user to program additional components when needed. Some of these components may later find their way into the corresponding library, which is thus strengthened by user contributions.
Some of the components contain full quantum mechanical treatment of the neutron as a wave on the microscopic length scales to compute the correct physics of the component, e.g. diffraction from a crystal. However, it should be emphasized that quantum mechanics is only present in the simulations at this level of description. The transport of rays between components is performed by classical kinematics, possibly including gravity.
Describing and visualizing the neutron instrument
It is the task of the user (the simulator) to assemble the components into a full working instrument. The Monte Carlo simulation itself is then performed by the simulation package on the basis of the instrument description.
All packages have features to visualize the instrument geometry, the simulated rays, and the monitor/detector data.
Varying and optimizing the instrument parameters
The packages give the opportunity to perform a series of simulations, where one or more instrument parameters are systematically varied. In this way, it is possible to perform a scan of one or more instrument parameters and plot some key data, e.g. the neutron counts in a monitor, as a function of the scanned parameter(s). The packages can automatically produce such plots.
In addition, some packages are able to vary a number of instrument parameters to perform optimization of the instrument settings. Many numerical optimization methods exist, and we will not here go into details. General about the optimizations is, however, that the user should define a certain Figure of Merit (FoM) for the optimizer to maximize. This could be the number of neutrons at the sample, the reciprocal of the beam spot size (if a narrow beam is wanted), the reciprocal width of the neutron energy distribution (if a monochromatic beam is desired), or any combination of these. The optimal parameter settings of course depend upon the choice of the FoM, and hence a careful selection is necessary.
Virtual experiments
Using a detailed instrument description with a realistic sample model, it is possible to produce a computer model of a complete neutron experiment. This virtual instrument can then be controlled with software that resembles the actual instrument control program, and the simulation data can be analyzed with the same tools as used for real experimental data. This is known as a virtual experiment. It is foreseen by many scientists in the field that virtual experiments can be used to support and complement experimental activities in a number of ways[7]:
- In the design phase of an instrument it can be investigated how the instrument will perform certain key experiments. This can in turn be used to optimize the instrument design[8].
- When applying for beam time at a facility, the experimentalists can estimate whether the experiment will be feasible at a given instrument and how much beam time is needed.
- Experiments (and experimentalists) can be prepared prior to performing the actual experiment by analyzing the optimal instrument configuration[9].
- Running experiments can be diagnosed "on the fly" to faster react on various mistakes and unexpected results.
- Analysis of the data can be conducted in more detail by including instrument-related features in the data analysis[10].
- New data analysis programs can be benchmarked against virtual data from known samples[11].
- Students and new users can be trained before their first actual experiment. This is, in fact, the general idea behind the simulation problems in these notes.
Performing the ray-tracing simulations
Since the (neutron) rays in the simulations are non-interacting and in principle statistically independent, the simulations can without methodological problems be carried out in parallel on several computers. Many packages are equipped to parallize the simulations automatically, and the performance has been seen to scale linearly with the number of processors up to at least 1000.
Hence, the technique of neutron ray-tracing simulations can take full advantage of the large parallel supercomputers emerging in many research facilities and universities.
- ↑ See the NISP home page http://www.paseeger.com
- ↑ See the IDEAS home page http://www.ornl.gov/~xwl/publications/NeutronNews-2002.pdf
- ↑ See the McStas home page http://www.mcstas.org
- ↑ See the VITESS home page http://www.hmi.de/projects/ess/vitess
- ↑ See the RESTRAX home page http://omega.ujf.cas.cz/restrax
- ↑ See the home page of the MCNSI part of NMI3 http://www.mcnsi.risoe.dk
- ↑ K. Lefmann et al. J. Neutr. Res. (in press) (2009).
- ↑ A. Vickery et al, J. Jap. Phys. Soc., in print (2013)
- ↑ P.K. Willendrup et al., Physica B, vol. 385-386, p. 1032-1034 (2006)
- ↑ L. Udby et al., Nucl. Instr. Meth. A, vol. 634, p. S138 (2011)
- ↑ P.L.W. Trigenna-Piggott, J. Neutr. Res., vol. 16, p. 13 (2008)
Techniques for neutron ray-tracing
The neutron ray-tracing packages have a very similar philosophy in the way simulations are described and performed, and in the way the neutrons are represented. We here describe this in some detail.
Representing the neutrons in simulations
In simulations, a neutron is represented semiclasically by simultaneously well-defined position, \({\bf r}\), velocity, \({\bf v}\), and and all three components of the neutron spin vector, \({\bf s}\). Formally, this violates the laws of quantum mechanics, in particular the Heisenberg uncertainty relations[1], given for the position/momentum coordinates by
\begin{equation}\label{dummy2120409709} \delta x \delta p \geq \dfrac{\hbar}{2} \end{equation}
However, as we shall illustrate in the problem Validity of the semiclassical approximation, the semiclassical approximation is very good for describing instruments that use "typical" neutrons with velocities of the order 0.1 - 10 km/s. One important region where the semiclassical approximations breaks down is for very slow (or "ultra-cold") neutrons, where quantum effects become prominent in the optical properties[2][3][4][5]. Ultra-cold neutrons will not be discussed in this version of the notes.
The validity of the semiclassical approach is discussed in detail in Ref. [6].
The neutrons are simulated in "rays", by which we mean the neutron trajectory; position \({\bf r}\), as a function of time \(t\). Therefore, at any point in the simulation of one ray, \(t\) is a necessary parameter. This is of particular importance when simulating pulsed neutron sources.
The neutron weight factor
To represent realistic values for neutron numbers, a neutron ray in general represents more than a single physical neutron. As a consequence, the ray contains an additional parameter, the weight factor, \(p\). This generally has the unit of neutrons per second. When the ray begins at the source, \(p\) has a typical initial value of thousands or millions neutrons per second.
To improve simulation speed, the weight factor can be manipulated through the simulation. For example, when some physical neutrons are "lost" due to e.g. finite reflectivity or absorption, the simulated ray will in general continue in the simulations, while \(p\) is adjusted to reflect the correct average physical behaviour. When (if) the neutron ray reaches the detector, \(p\) may be only a fraction of a neutron per second. This weight factor adjustment is a very efficient implementation of importance sampling, as presented in the section Introduction to the Monte Carlo technique.
To quantify the method, we consider a certain position (a surface perpendicular to the beam) in the simulated instrument. Here, the neutron intensity is given by the sum of all rays reaching this surface (again with units neutrons per second):
\begin{equation}\label{dummy945804845} I_j = \displaystyle\sum_{i=1}^N p_{i,j-1} \end{equation}
where \(i\) is the ray index, \(N\) is the total number of rays, and \(j\) is the index of the given component. The index \(j-1\) on \(p\) indicate that we consider the intensity being emitted by the previous component. If the ray does not reach this point, we take \(p_{i,j-1}=0\). The weight of the neutrons emitted from this point in the simulations, i.e. after interacting with component \(j\), is expressed by
\begin{equation}\label{dummy653998044} p_j = w_j p_{j-1} ,\, \end{equation}
where the ray index, \(i\), is omitted for simplicity. The weight multiplier of the \(j\)'th component, \(w_j\), is calculated by the probability rule
\begin{equation}\label{eq:weight_master} f_{\rm MC, b} w_j = P_{\rm b} , \, \end{equation}
where \(P_{\rm b}\) is the physical probability for the event "b", and \(f_{\rm MC,b}\) is the probability that the Monte Carlo simulation selects this event.
Often, there is only one allowed event, giving \(f_{\rm MC}=1\), whence \(w_j=P\). This may, e.g., be the case for neutrons being attenuated when passing through absorbing materials. When a Monte Carlo branch point is reached (selection between several events), we have \(f_{\rm MC, b} < 1\) for each branch, b. However, since \(f_{\rm MC}\) is a probability function, we must have
\begin{equation}\label{dummy540191185} \displaystyle\sum_b f_{\rm MC, b} = 1 . \, \end{equation}
Estimates of simulation uncertainty
In a stochastical simulation, it is important to be able to estimate the uncertainty, in the same way as for experiments. We here present a simple derivation of the uncertainty in simulations with weight factors.
As a simple start, let us imagine \(M\) rays, all with weight factor \(p\). Each ray is imagined to have an overall probability, \(P_{\rm d}\), of reaching the detector. The distribution of observed rays will be binominally distributed with a mean value \(\bar{N} = MP_{\rm d}\) and variance \(\sigma^2(N) = M P_{\rm d} (1-P_{\rm d})\). Very often, we will have small values of \(P_{\rm d}\) and large values of \(M\), so that \(M P_{\rm d} \gg 1\). Here, it is valid to approximate the distribution as a Gaussian with standard deviation
\begin{equation}\label{dummy730577740} \sigma(N) = \sqrt{MP_{\rm d}} = \sqrt{N} , \end{equation}
where the observed value, \(N\), is used as the best estimate for the average, \(\bar{N}\). Recalling that the rays have weight factors, the total simulated intensity will in this case be
\begin{equation}\label{dummy185225129} I=Np, \, \end{equation}
with a variance
\begin{equation}\label{eq:MCerror1} \sigma^2(I) = Np^2 . \, \end{equation}
Imagine now that the rays can have a number of (discrete) different weight factors, \(p_i\). The simulated number of rays in each class is denoted \(n_i\) (standard deviation \(\sqrt{n_i}\)). The total simulated result is now
\begin{equation}\label{dummy2068296395} I = \displaystyle\sum_i n_i p_i . \, \end{equation}
Using that the variance of a sum is the sum of variances, we reach the statistical error of the simulated result:
\begin{equation} \label{eq:MCerror2} \sigma^2(I) = \displaystyle\sum_i n_i p_i^2 . \end{equation}
Now, let the simulations occur with rays of arbitrary weight factors, \(p_j\), different for each ray, i.e. \(n_i \equiv 1\), corresponding to a continuous distribution of \(p_i\). If the distribution of these weight factors is reasonably well behaved, we can generalize the equations above to reach
\begin{equation}\label{dummy2014930404} I = \displaystyle\sum_i p_i , \, \end{equation}
with a statistical error:
\begin{equation} \label{eq:MCerror_final} \sigma^2(I) = \displaystyle\sum_i p_i^2 , \end{equation} which is consistent with \eqref{eq:MCerror1} and \eqref{eq:MCerror2}. This is the way uncertainties of simulation results are calculated in all detectors (sometimes denoted monitors) in the McStas package.
Scattering from a sample
The place where most Monte Carlo choices are made is when the neutron ray interacts with a sample. First, it must be decided whether the ray scatters or not. If scattering takes place, the algorithm must select the point in the sample for the scattering event, the scattered direction, and (for inelastic scattering) the final energy. Finally, there is potentially an issue of multiple (repeated) scattering.
To simplify the description, let us just study the scattering direction. Assume we have a sample that only scatters elastically and isotropically with volume specific cross section \(\Sigma\) and has no absorption. Then, the attenuation factor is \(\mu = \Sigma\), and the physical probability for scattering is
\begin{equation}\label{dummy547165093} P_{\rm scatt} = 1-\exp(-\Sigma L) , \, \end{equation}
where \(L\) is the length of the particular ray within the sample. However, we must also consider the outgoing ray. The probability for scattering into the solid angle \(d\Omega\) is
\begin{equation}\label{dummy1409330943} P(\Omega) d\Omega = P_{\rm scatt.} \dfrac{d\Omega}{4\pi} . \end{equation}
Let us require that the ray must always scatter, and let us select the outgoing ray direction with uniform probability (the "physical" scattering). Then we have
\begin{equation}\label{dummy469886538} f_{\rm MC\, phys.} d\Omega = \dfrac{d\Omega}{4\pi} , \end{equation}
and equation \eqref{eq:weight_master} gives
\begin{equation} \label{eq:w_simple} w_{\rm phys.} = \dfrac{P(\Omega)d\Omega}{f_{\rm MC\, phys.}d\Omega} = 1-\exp(- \Sigma L) \approx \Sigma L , \end{equation}
where the rightmost approximation is valid only for "thin" samples, \(\Sigma L \ll 1\). Note that we have not taken into account the attenuation of the outgoing neutron ray.
Focusing in sample scattering
Some neutron instruments have a geometry such that only rays scattered in certain "interesting directions" have any chance of being detected. In such cases, one will employ the technique of focusing to improve simulation efficiency. This implies a need to modify \eqref{eq:w_simple}, as we discuss below.
In focusing, the ray will be emitted only within a certain solid angle, \(\Delta \Omega\). This solid angle must contain all the directions contributing to the detector counts, otherwise the focusing will give wrong results. Assuming uniform selection within \(\Delta \Omega\), the Monte Carlo probability will be given by
\begin{equation}\label{dummy1611418157} f_{\rm MC\, focus} d\Omega = \dfrac{d\Omega}{\Delta \Omega} , \end{equation}
and equation \eqref{eq:weight_master} gives
\begin{equation}\label{dummy686215173} w_{\rm focus} = \dfrac{P_{\rm scatt.}}{f_{\rm MC\, focus}} = \dfrac{\Delta\Omega}{4\pi} \big(1-\exp(- \Sigma L) \big) \approx \dfrac{\Delta\Omega}{4\pi}\Sigma L . \end{equation}
Comparing to the physical case, the focusing method gives smaller weight factors per ray, but a larger number of rays traveling towards the detector. This gives the same final result, but with a smaller statistical error. The focusing technique is an important example of variance reduction through importance sampling.
- ↑ E. Merzbacher. Quantum Mechanics. (Wiley, 1998)
- ↑ V.V. Nesvizhevsky et al. Nature, vol. 415, p. 297. (2002)
- ↑ R. Golub. Rev. Mod. Phys., vol. 68, p. 329. (1996)
- ↑ Y. Hasegawa et al. Nature, vol. 425, p. 45. (2003)
- ↑ K. Kirch, B. Lauss, P. Schmidt-Wellenburg, G. Zsigmond. Nuclear Physics News, vol. 1, p. 1. (2010)
- ↑ F. Mezei. Lecture Notes of the Introductory Course to the ECNS99. The Basic Physics of Neutron Scattering Experiments, p. 27-39. (Report KFKI-1999-04/E)
← Previous page: Inelastic magnetic scattering
→ Exercises: Exercises in Monte Carlo simulations
→ Next page: McStas simulation projects