Diffraction from a powder
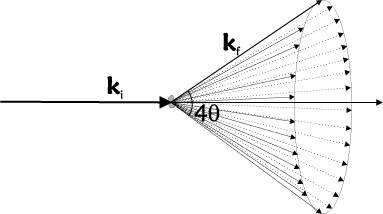
In a powder, there are billions of randomly oriented crystal grains, typically of \(\mu\)m size. Hence, it is safe to assume that all lattice orientations are represented equally and that extinction effects are absent (see the sections on Crystal mosaicity; secondary extinction and Perfect crystals; primary extinction). Bragg scattering of an incoming monochromatic beam will thus happen in all possible ways that fulfill the Bragg law in equation \eqref{eq:bragg}. The resulting scattering will occur on cones of opening angles of \(4\theta\), the Debye-Scherrer cones. This is illustrated in Figure xx--CrossReference--fig:DScone--xx.
To obtain the total scattering cross section from a powder, we average the cross section from equation \eqref{eq:bragg_half_int} over all orientations of a given lattice vector, \({\boldsymbol\tau}\). We use polar coordinates, \((\phi,\omega)\), where \(\omega\) is the angle between \({\bf k}_{\rm i}\) and \(\boldsymbol\tau\) as in Figure xx--CrossReference--fig:scatteringplane--xx and \(\phi\) is the (unimportant) rotation angle around \({\bf k}_{\rm i}\).
\begin{align} \label{eq:powdercros0} \sigma_{\tau} &= \frac{1}{4\pi} \int \sigma_{\boldsymbol\tau} d\Omega = \frac{1}{4\pi} \int \sigma_{\boldsymbol\tau} d\phi \sin(\omega) d\omega\nonumber \\ &= \dfrac{N (2\pi)^3}{V_0} \dfrac{2}{k_{\rm i}} \exp(-2W) \left| F_{\rm N}({\boldsymbol\tau})\right|^2 \dfrac{1}{4\pi} \displaystyle\int 2\pi \sin(\omega) \delta(\tau^2-2k_{\rm i}\tau\cos(\omega)) d\omega \nonumber\\ &= V \exp(-2W) \dfrac{1}{V_0^2} \dfrac{\lambda^3}{4 \sin\theta} j_\tau \left| F_{\rm N}({\boldsymbol\tau}) \right|^2 .\nonumber \end{align}
In the last step, we have included \(j_\tau\), which is the multiplicity of the reflection, meaning the number of crystallographically equivalent lattice planes that all contribute to the scattering. One example is the cubic \((100)\) reflection, with crystallographically equivalent reflections \((010)\), \((001)\), \((\bar{1}00)\), \((0\bar{1}0)\), and \((00\bar{1})\), giving \(j_{100}=6\).
In high-symmetry crystal structures, there may be non-equivalent reflections with the same length of \({\boldsymbol\tau}\). Examples are the cubic \((221)\) and \((300)\) reflections - and the cubic \((333)\) and \((511)\) reflections. In a powder, there is no way to separate these contributions to the scattering. Hence, to reach a description of the scattered intensity at a particular value of \(q\), we must sum over all reflections of same length of \(\tau\), reaching
\begin{equation}\label{eq:powdercross} \sigma_{q} = \displaystyle\sum_{|{\boldsymbol\tau}|=q} \sigma_{ {\boldsymbol\tau}} = V \exp(-2W) \dfrac{1}{V_0^2} \dfrac{\lambda^3}{4 \sin\theta} \displaystyle\sum_{|{\boldsymbol\tau}|=q} j_\tau \left| F_{\rm N}({\boldsymbol\tau}) \right|^2 . \end{equation}
Experimental considerations
A closer look at equation \eqref{eq:powdercross} reveals that the only sample-dependent quantity is the nuclear structure factor, \(F_{\rm N}({\boldsymbol\tau})\). It is thus possible to determine the relative nuclear structure factor for a number of reflections from the relative intensity of the scattered neutrons. This can be used to determine the position of the atoms within the unit cell. The size and shape of the unit cell (the lattice parameters) are, in turn, determined by the position of the reflections, via the Bragg law. A number of standard programs exist to perform this analysis.